The Allocation of Shared Fixed Costs Fairness versus

The Allocation of Shared Fixed Costs Fairness versus Efficiency H. Paul Williams Martin Butler - London School of Economics - University College Dublin

The Basic Problem Given a Set of Facilities (E. G. Swimming Pools, Libraries, Aircraft Runways, Electric Generators, Reservoirs Etc. ) 1. 2. Which Do We Build? How Do We Split Their Fixed Costs Between the Users Efficiently or Fairly?

An Example Six Potential Facilities {1, 2, 3, 4, 5, 6} Some of Which are Needed by These Potential Customers {A, B, and C}

An Example Customer A requires 1 of {1, 2, 3} and 1 of {4, 5, 6} Customer B requires 1 of {1, 4} and 1 of {2, 5} Customer C requires 1 of {1, 5} and 1 of {3, 6} Benefits to 3 customers of being catered for 8, 11, 19 Fixed costs of 6 facilities 8, 7, 8, 9, 11, 10

A 0 -1 Integer Programming Model Maximise Subject to

Dual of the LP Relaxation Minimise Subject to Vi. X is amount of cost from ith group of facilities allocated to customer X UX is surplus benefit accruing to customer X

NB: 1. Each customer pays within its means 2. If a facility not totally paid for it is not built (LP dualilty) This ‘would’ be a satisfactory allocation if a fractional solution were acceptable (a) No customer pays more than would by alternate provision (a)(b) Total cost of facilities built met by customers

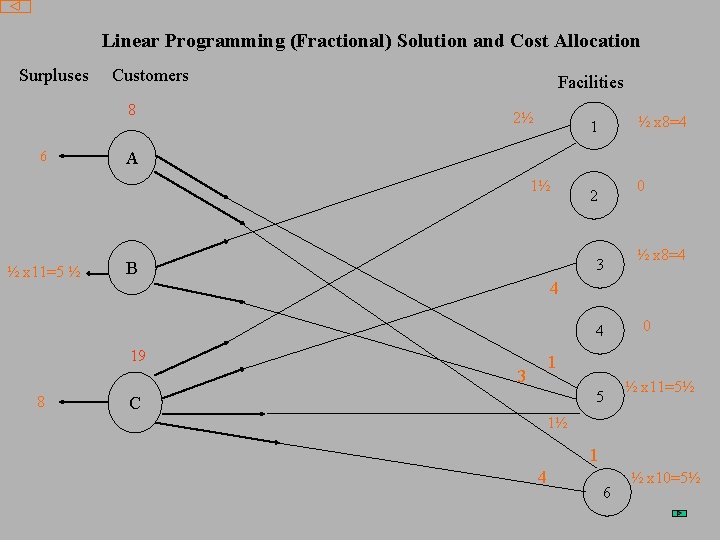
Linear Programming (Fractional) Solution and Cost Allocation Build ½ of each of facilities 1, 3, 5, 6 to serve customers A and C and ½ of customer B , Revenue – Cost = 14 Solution is neither integral nor fair This would be a ‘satisfactory’ cost allocation if associated solution were integral

Costs Applied to Constraints Maximise Subject to Prices 2 5 6 3 8 6 8

Linear Programming (Fractional) Solution and Cost Allocation Surpluses Customers 8 6 Facilities 2½ A 1½ ½ x 11=5 ½ ½ x 8=4 1 0 2 3 B 4 4 19 0 1 3 8 ½ x 8=4 5 C ½ x 11=5½ 1½ 1 4 6 ½ x 10=5½

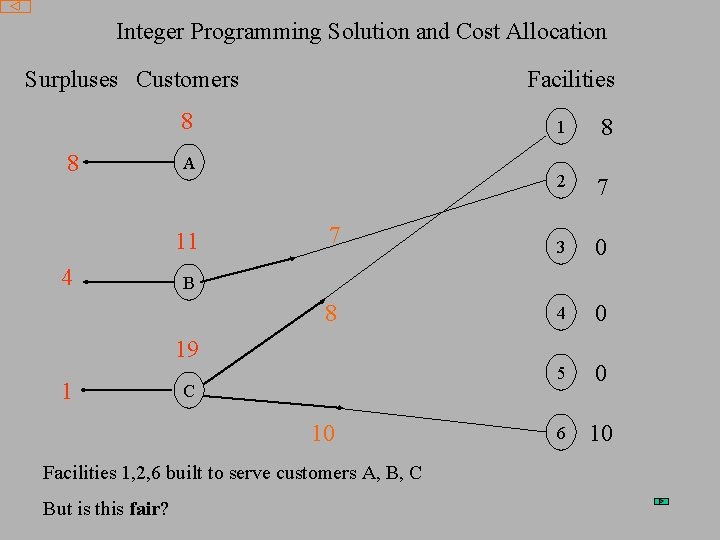
Optimal Integer Programming Solution Build Facilities 1, 2, 6 Serve Customers A, B, C Revenue - Cost = 13 Is there a cost allocation which will 1. Pay for facilities 1, 2, 6 2. Leave customers with net revenue of 13 3. Make facilities 3, 4, 5 uneconomic? 4. NO - Duality Theorem of Linear

Dual Values and the Allocation of Costs If constraint binding in LP satisfied as equality Hence total cost compensation to facilities (in equal amounts) equals amount paid by customer

But if constraint binding in IP (non redundant and has positive economic value) will have positive ‘dual value’ but not necessarily satisfied as equality. Hence Cost allocations may not balance

Possible Methods of Cost Allocation 1. (Sub additive) Price Function instead of Prices Obtain by appending (Chvátal) Cutting Planes obtained by: (i) Adding constraints in suitable multiples (ii) Nested Rounding of resultant right-hand-sides ‘Pays for’ facilities and charges customers appropriately but costs do not ‘balance’

Possible Methods of Cost Allocation 2. Gomory-Baumol Prices obtained by only considering multipliers in (i) Satisfies only some requirements of cost allocation e. g. Necessary to subsidise some activities

Derivation of Price Function Append This Cutting Plane To Model Resultant Linear programme Yields Integer Solution

Corresponding Dual Solution Implies Price Function on Coefficients Column of Model. in Each Such a Price Function is Known as a ‘Chvátal Function’ These are the Discrete Analogy of Dual Values (Shadow Prices) for Linear Programmes

A Typical Chvatál Function b 1 Multiply b 2 2 Divide & Round Down Multiply 1 17 3 1 Divide & Round Down Multiply b 2 2 3 Chvátal Function is Relaxation is Would be Linear Programming Dual Values (Shadow Prices)

Uses for Price Functions 1. Charge Customers 2. A: 3. Charge & Excess 4. B: =8 =9 C: =19 3. 1: =8 4. 2: =7 (round up 5. 3: =7 ½ (don’t build) 6. 4: =9 (round up 7. 5: =11 8. 6: =10 2. Pay for Facilities necessary) 9. 10. NB Solution is Degenerate. We Build Facilities 1, 2, 6 but Don’t Build 4, 5 (Although Just Paid For. ) In Order to Recover Full Cost of Facility 4 We Need to Round Up.

Uses for Price Functions 3. Price a New Facility E. g A New Facility Which Would Substitute For: The 2 nd Set of A’s Needs The 1 st Set of B’s Needs The 2 nd Set of C’s Needs Payment Required = 16 ½ If Cost Below This: Build If Cost Equal: Marginal If Cost Higher: Don’t Build

Optimal Solution is to Build Facilities 1, 2, 6 (Facility 3 ‘Priced Out, ’ Facilites 4, 5 ‘Just’ Not Worth Building (Degenerate Solution) ) Total Cost of Facilities 25 Supply Customers A, B, C Total Price Paid (Benefits Less Excess)

A More Satisfactory Cost Allocation Only include facilities to be built (with hindsight) in model i. e. Facilities 1, 2, 6 Solve LP relaxation to give integer solution Hence dual solution will be ‘sensible’

Integer Programming Solution and Cost Allocation Surpluses Customers Facilities 8 8 8 2 7 7 3 0 8 4 0 5 0 6 10 A 11 4 1 B 19 1 C 10 Facilities 1, 2, 6 built to serve customers A, B, C But is this fair?

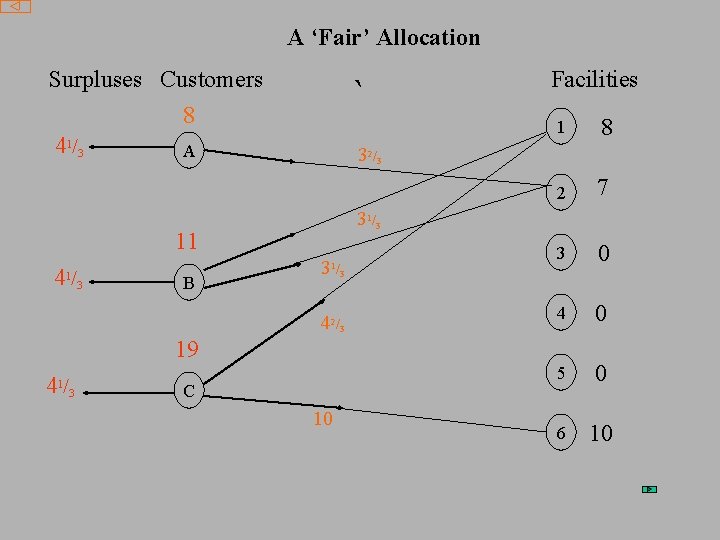
Obtaining a Fair Allocation The allocation given lies in the core of possible allocations i. e. no customer pays more towards facilities than they would by alternate provision The dual solution (to restricted LP) will, however, be an extreme solution in core To be fair we could instead Minimise maximum surplus Such a solution should lie at the centre of the core i. e. in the Nucleolus

A ‘Fair’ Allocation Surpluses Customers 8 41/3 A ` B 1 8 2 7 3 0 4 0 5 0 6 10 32/3 31/3 11 41/3 Facilities 3 1/ 3 42/3 19 4 /3 1 C 10

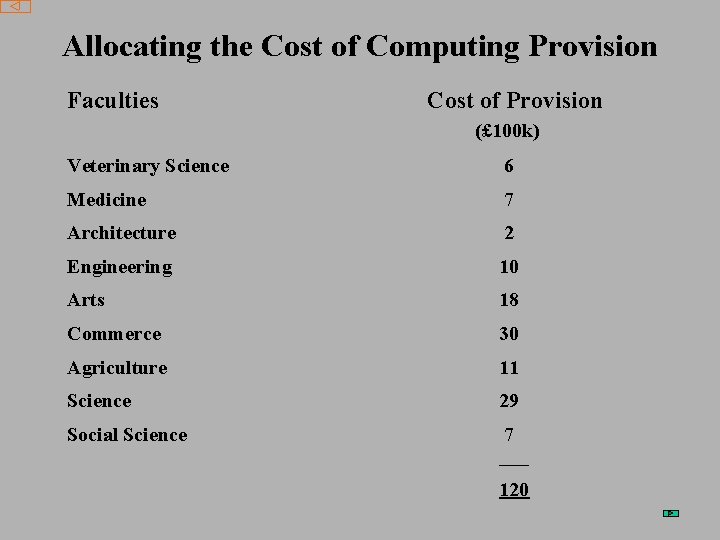
Allocating the Cost of Computing Provision Faculties Cost of Provision (£ 100 k) Veterinary Science 6 Medicine 7 Architecture 2 Engineering 10 Arts 18 Commerce 30 Agriculture 11 Science 29 Social Science 7 ___ 120

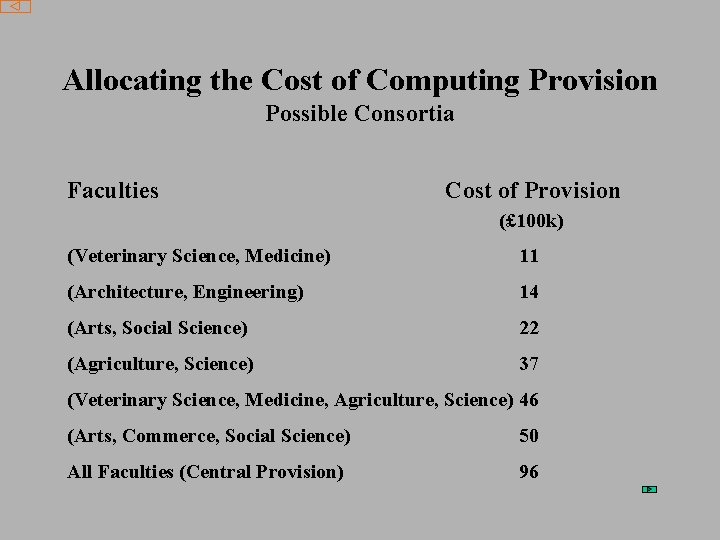
Allocating the Cost of Computing Provision Possible Consortia Faculties Cost of Provision (£ 100 k) (Veterinary Science, Medicine) 11 (Architecture, Engineering) 14 (Arts, Social Science) 22 (Agriculture, Science) 37 (Veterinary Science, Medicine, Agriculture, Science) 46 (Arts, Commerce, Social Science) 50 All Faculties (Central Provision) 96

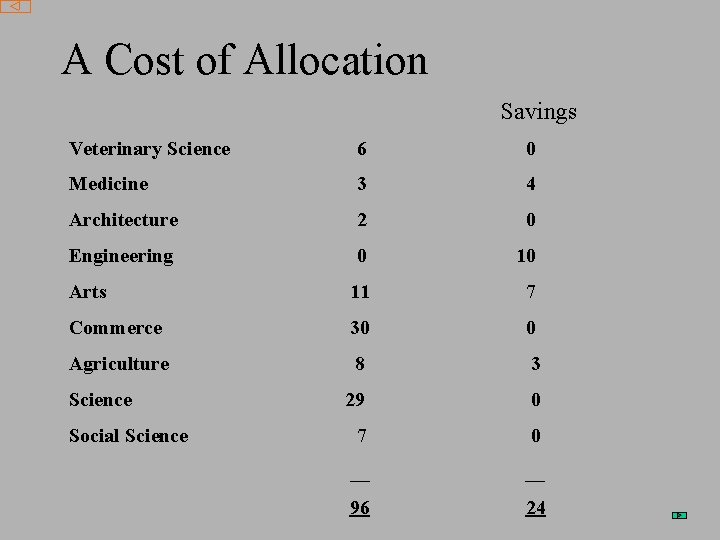
It was decided that all faculties should use central provision. How do we split the cost of 96 between the faculties? NB Savings over sum of individual provision is 24 How do we ‘share the savings’?

A Cost of Allocation Savings Veterinary Science 6 0 Medicine 3 4 Architecture 2 0 Engineering 0 10 Arts 11 7 Commerce 30 0 Agriculture 8 3 29 0 7 0 __ __ 96 24 Science Social Science

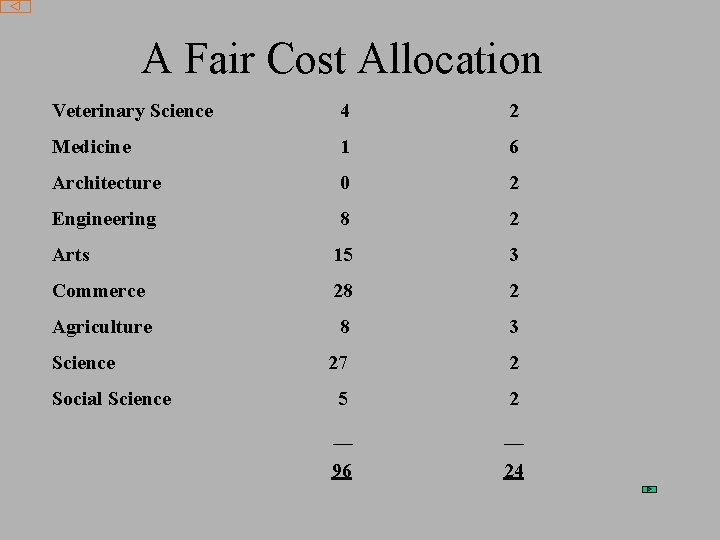
Fair allocation tries to equalise savings over all possible (including individual) consortia

A Fair Cost Allocation Veterinary Science 4 2 Medicine 1 6 Architecture 0 2 Engineering 8 2 Arts 15 3 Commerce 28 2 Agriculture 8 3 27 2 5 2 __ __ 96 24 Science Social Science

Experiments in Social Choice Theory suggest that when allocating limited resources subject to need minimising maximum excess (i. e. trying to equalise benefits) is most acceptable to most people.

References M. Butler & H. P. Williams, Fairness versus Efficiency in Charging for the Use of Common Facilities, Journal of the Operational Research Society, 53 (2002) M. Butler & H. P. Williams, The Allocation of Shared Fixed Costs, European Journal of Operational Research, 170 (2006) J. Broome, Good, Fairness and QALYS, Philosophy and Medical Welfare, 3 (1988) J. Rawls, A Theory of Justice, Oxford University Press, 1971 J. Rawls & E. Kelly Justice as Fairness: A Restatement Harvard University Press, 2001 M. Yaari & M. Bar-Hillel, On Dividing Justly, Social Choice Welfare 1, 1984