The Algebra of Encryption CS 6910 Semester Research

The Algebra of Encryption CS 6910 Semester Research and Project University of Colorado at Colorado Springs By Cliff Mc. Cullough 18 July 2011

Modern Cryptography 7/16/2011 Cliff Mc. Cullough 2

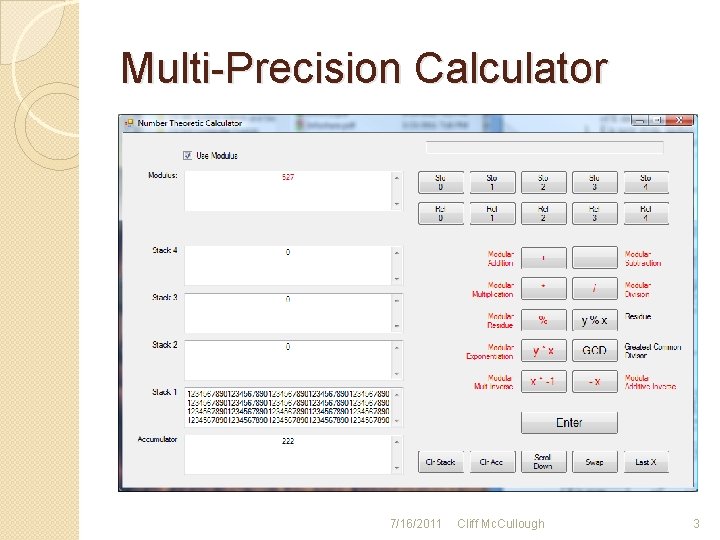
Multi-Precision Calculator 7/16/2011 Cliff Mc. Cullough 3

That’s a lot of digits 7/16/2011 Cliff Mc. Cullough 4

Modular Arithmetic �The Division Algorithm a=mb+r “Any integer a can be divided by b in such a way that the remainder is smaller than b. ” (Burton, 2007, p. 17) 7/16/2011 Cliff Mc. Cullough 5

Examples � 13 = 1 * 12 + 1 ◦ 13 ≡ 1 mod 12 � 9 = 0 * 12 + 9 ◦ 9 ≡ 9 mod 12 7/16/2011 Cliff Mc. Cullough 6

Addition �First express the numbers in modular form �Add the numbers and collect the terms �Adjust the multiplier if needed so that the residue is positive and less than the modulus 7/16/2011 Cliff Mc. Cullough 7

Subtraction �First express the numbers in modular form �Subtract the numbers and collect the terms �Adjust the multiplier if needed so that the residue is positive and less than the modulus 7/16/2011 Cliff Mc. Cullough 8

Multiplication �Multiplication is merely repeated addition �Adjust the multiplier so that the residue is positive and less than the modulus 7/16/2011 Cliff Mc. Cullough 9

Division �Division is tricky �Instead of c ---- = e d �We write c = d * e �Ask by what number, e, can we multiply d to result in c, in modular arithmetic? 7/16/2011 Cliff Mc. Cullough 10

Division by Multiplicative Inverse �Another way to divide is to multiply by the MMI c * d-1 = e �MMI: d * d-1 ≡ 1 modulus �Ask by what number, d-1 , can we multiply d such that the result is 1 in modular arithmetic? 7/16/2011 Cliff Mc. Cullough 11

Useful Functions �Euclidean Algorithm ◦ Greatest Common Divisor ◦ Modular Multiplicative Inverse �Modular Exponentiation �Chinese Remainder Theorem �Euler’s Totient Function 7/16/2011 Cliff Mc. Cullough 12

Greatest Common Divisor �Compare the smaller number to the larger �Find the quotient of the two numbers �Multiply the smaller by the quotient and subtract �Now compare the residue with the previous smaller number �Continue until the residue is zero 7/16/2011 Cliff Mc. Cullough 13

GCD Example from (Euclidean algorithm, 2011) 7/16/2011 Cliff Mc. Cullough 14

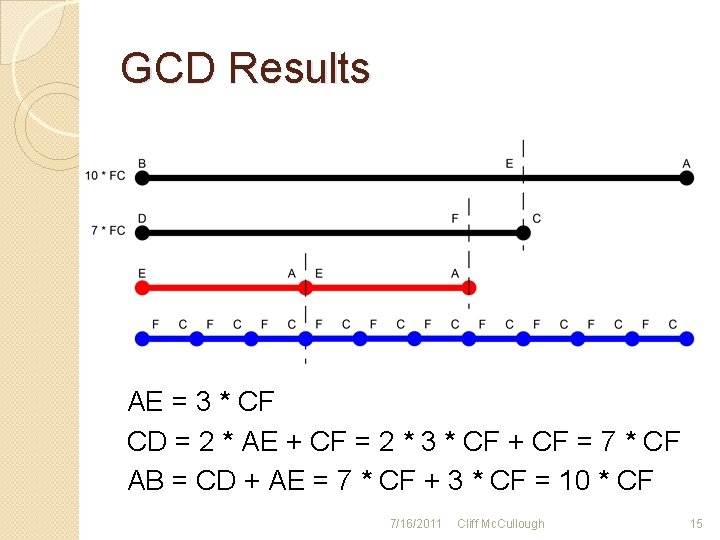
GCD Results AE = 3 * CF CD = 2 * AE + CF = 2 * 3 * CF + CF = 7 * CF AB = CD + AE = 7 * CF + 3 * CF = 10 * CF 7/16/2011 Cliff Mc. Cullough 15

Extended Euclidean Algorithm �Use Extended Euclidean Algorithm �Basically keep track of the coefficients 1. Start by writing the two numbers 2. Find the quotient 3. Multiply the second equation by the quotient and subtract from the first 4. Repeat steps 2 and 3 until the residue is zero 7/16/2011 Cliff Mc. Cullough 16

Extended Euclid Example � 50 = 50 ( 1) + 35 ( 0) � 35 = 50 ( 0) + 35 ( 1), q = 1 � 15 = 50 ( 1) + 35 ( -1), q = 2 � 5 = 50 ( -2) + 35 ( 3), q = 3 � 0 = 50 ( 7) + 35 (-10) 7/16/2011 Cliff Mc. Cullough 17

Finding the MMI � 13 = 13 ( 1) + 4 ( 0) � 4 = 13 ( 0) + 4 ( 1), q = 3 � 1 = 13 ( 1) + 4 ( -3) � 1 = 13 (1) + 4 (-3) + 13 (-4) + 4 (13) � 1 = 13 (1 - 4) + 4 (-3 + 13) � 1 = 13 (-3) + 4 (10) 7/16/2011 Cliff Mc. Cullough 18

Modular Exponentiation �Initiate X = base, E = exponent, Y = 1 �If E is odd ◦ Replace Y = X * Y ◦ Replace E = E - 1 �E is not even ◦ Replace X = X * X ◦ Replace E = E ÷ 2 �When E = 0, Y is the answer (Garrett, 2004, p. 123) 7/16/2011 Cliff Mc. Cullough 19

Exponentiation Example E = 11 = 8 + 2 + 1 Y = 38 * 32 * 31 = 6561 * 9 * 3 Notes Initialization E is odd E is even E is odd X 3 E 11 10 5 4 2 1 0 9 81 6561 7/16/2011 Cliff Mc. Cullough Y 1 3 27 177147 20

Modular Exponentiation Example E = 11 = 8 + 2 + 1 Y = 38 * 32 * 31 = 237 * 9 * 3 mod 527 Notes Initialization E is odd E is even E is odd X 3 E 11 10 5 4 2 1 0 9 81 237 7/16/2011 Cliff Mc. Cullough Y 1 3 27 75 21

Consider Multiplication 1111 x 1111 --------1111 + 1111 --------11100001 11 x 11 -------11 + 11 -------1001 7/16/2011 Cliff Mc. Cullough 22

Chinese Remainder Theorem �Reduces calculation time by dealing with smaller numbers �Some elements may be pre-calculated and used repeatedly for subsequent calculations 7/16/2011 Cliff Mc. Cullough 23

How To CRT �Pre-calculations ◦ ◦ Know the Factors of M Calculate each Mi Calculate MMI of each Mi mod mi Calculate Ai �Perform the operation �Combine the results (Stallings, 2011, pp. p 254 -257) 7/16/2011 Cliff Mc. Cullough 24

CRT Pre-calculations �Chose m 1 and m 2 M = m 1 * m 2 = 37 * 49 = 1813 �Calculate Mi = M ÷ m i M 1= 1813 ÷ 37 = 49 M 2 = 1813 ÷ 49 = 37 �Calculate Mi-1 mod mi M 1 -1 mod m 1 = 49 -1 mod 37 ≡ 34 M 2 -1 mod m 2 = 37 -1 mod 49 ≡ 4 7/16/2011 Cliff Mc. Cullough 25

CRT Pre-calculations too �Calculate Ai A 1 = M 1 * M 1 -1 mod M = 49 * 34 mod 1813 ≡ 1666 A 2 = M 2 * M 2 -1 mod M = 37 * 4 mod 1813 ≡ 148 7/16/2011 Cliff Mc. Cullough 26

CRT Addition �Compute x + y = zi mod mi for each mi 973 mod 37 = 11 + 678 mod 37 = 12 --------z 1 = 23 mod 37 �Combine 973 mod 49 = 42 + 678 mod 49 = 41 --------z 2 = 34 mod 49 results (x + y) mod M = (z 1 * A 1 + z 2 * A 2) mod M (973 + 678) mod 1813 = (23 * 1666 + 34 * 148) mod 1813 ≡ 1651 7/16/2011 Cliff Mc. Cullough 27

CRT Multiplication �Compute x * y = zi mod mi for each mi 973 mod 37 = 11 973 mod 49 = 42 * 678 mod 37 = 12 --------z 1 = 14 mod 37 * 678 mod 49 = 41 --------z 2 = 32 mod 49 �Combine results (x * y) mod M = (z 1 * A 1 + z 2 * A 2) mod M (973 + 678) mod 1813 = (14 * 1666 + 32 * 148) mod 1813 ≡ 865 7/16/2011 Cliff Mc. Cullough 28

Euler’s Totient Function Euler’s totient function, Φ(n), identifies the number of integers, less than n, that are relatively prime to n. A good treatment of Euler’s Totient function can be found in (Burton, 2007, pp. 131 -135). Φ(n)=(pi)*(qj)=(pi - pi-1)*(qj - qj-1) (Burton, 2007, pp. 131 -135) 7/16/2011 Cliff Mc. Cullough 29

Phi Examples 21 = 3 * 7 Φ(21)=(3 - 1) * (7 - 1) = 2 * 6 = 12 � 1, 2, 4, 5, 8, 10, 11, 13, 16, 17, 19, 20 are the 12 numbers less than 21 that are coprime to 21 20 = 4 * 5 Φ(21)=(22 -21) * (51 -50) = (4 -2)*(5 -1)=2*4=8 �The 8 integers less than 20 coprime to 20 are 1, 3, 7, 9, 11, 13, 17, 19 7/16/2011 Cliff Mc. Cullough 30

Public Key Cryptography RSA �RSA uses Euler’s theorem �If a and n are coprime �then aΦ(n) ≡ 1 mod n (Burton, 2007, p. 137) 7/16/2011 Cliff Mc. Cullough 31

How to RSA �Chose two prime numbers p and q �Form n = p * q and find Φ(n) �Choose encryption exponent e coprime to Φ(n) �Find MMI of e mod Φ(n) �Encrypt: C = Me mod n �Decrypt: M = Cd mod n 7/16/2011 Cliff Mc. Cullough 32

Why Does RSA Work �C = Me mod n �M = (C)d = Me*d mod n �e and d were chosen such that e * d ≡ 1 mod Φ(n), therefore: e * d = m * Φ(n) + 1 �Remember the Euler’s Theorem MΦ(n) ≡ 1 mod n �Me*d = MmΦ(n)+1 = (MΦ(n))m * M ≡ 1 m * M mod n 7/16/2011 Cliff Mc. Cullough 33

RSA and CRT �To use CRT, we need to know the factors of n �Thus, we only use CRT to decrypt 7/16/2011 Cliff Mc. Cullough 34

RSA Example �Let: p = 17 q = 31 e = 11 message: M = 3 n = p * q = 17 * 31 = 527 Φ(n) = 16 * 30 = 480 d = e-1 mod Φ(n) ≡ 131 7/16/2011 Cliff Mc. Cullough 35

RSA-CRT Pre-calculations P = n ÷ p = 31 P-1 mod p ≡ 11 Ap = P * P-1 mod n = 31 * 11 mod 527 ≡ 341 Q = n ÷ q = 17 Q-1 mod q ≡ 11 Aq = Q * Q-1 mod n = 17 * 11 mod 527 ≡ 187 dp = d mod Φ(p) = 131 mod 16 ≡ 3 dq = d mod Φ(q) = 131 mod 30 ≡ 11 7/16/2011 Cliff Mc. Cullough 36

RSA Encrypt �Encrypt is standard C = Me mod n = 311 mod 527 ≡ 75 7/16/2011 Cliff Mc. Cullough 37

RSA-CRT Decrypt �Decrypt uses CRT ◦ Complete the operation Mp = Cdp mod p = 753 mod 17 ≡ 3 Mq = Cdq mod q = 7511 mod 31 ≡ 3 ◦ Combine the results M = (Mp * Ap + Mq * Aq) mod n = (3 * 341 + 3 * 187) mod 527 ≡ 3 7/16/2011 Cliff Mc. Cullough 38

How to Share a Secret �(Shamir, November, 1979) describes how to share a secret �A simple way of looking at this is to use a curve described by a polynomial function f(x) = atxt + at-1 xt-1. . . a 1 x + a 0 �Typically a 0 is the secret information �a 1 through at are chosen randomly 7/16/2011 Cliff Mc. Cullough 39

Why It Is Secret �We have t + 1 unknowns ◦ the t + 1 coefficients �We need t + 1 points on the curve to identify all the coefficients �The secret shares are points on the curve ◦ x, f(x) number pairs ◦ x can be an index. Only f(x) must be secret 7/16/2011 Cliff Mc. Cullough 40

Paillier Cryptography �Carmichael function is very similar to Euler’s totient function λ(n) = lcm(p-1, q-1) �Useful properties wλ ≡ 1 mod n wλn ≡ 1 mod n 2 �Which implies wλ = an + 1 wλn = bn 2 + 1 (Paillier, 1999) 7/16/2011 Cliff Mc. Cullough 41

How to Paillier �Choose two safe primes p and q �Calculate n = p * q and λ(n) �Define the function u-1 L(u) = -----n �Choose a generator value g such that L(gλ mod n 2) and n are coprime �Public key is (g, n) �Private key is λ 7/16/2011 Cliff Mc. Cullough 42

Paillier Encrypt �For plaintext message m < n �Chose a random number r < n �Encrypt c = gmrn mod n 2 7/16/2011 Cliff Mc. Cullough 43

Paillier Decrypt �Decrypt L(cλ mod n 2) m = --------- mod n L(gλ mod n 2) 7/16/2011 Cliff Mc. Cullough 44

The Generator g �Start from the Carmichael function gλ = 1 + an gλx = (1 + an)x �Use binomial expansion (1+an)x=1 + x(an) + n 2. . . �Result gλx = (1 + an)x = (1 + xan) mod n 2 7/16/2011 Cliff Mc. Cullough 45

Decrypt Numerator cλ - 1 gλmr λ n - 1 L(cλ mod n 2) = ---- mod n 2 = ------- mod n 2 n n �Applying the Generator g Result and Carmichael function L(cλ mod n 2) = ma mod n 2 7/16/2011 Cliff Mc. Cullough 46

Decrypt Denominator gλ - 1 (1 + an) - 1 L(gλ mod n 2) = ---- mod n 2 = ------- mod n 2 n n L(cλ mod n 2) = a mod n 2 7/16/2011 Cliff Mc. Cullough 47

The Decrypt Result �Combining the results gives L(cλ mod n 2) ma mod n 2 m = --------- mod n = -------- mod n L(gλ mod n 2) a mod n 2 7/16/2011 Cliff Mc. Cullough 48

Cryptographic Blinding �Cryptographic blinding allows for a message to be multiplied by a specially treated random number, while still allowing the message to be decrypted without knowledge of the random number. (Blinding (cryptography), 2011) 7/16/2011 Cliff Mc. Cullough 49

Paillier Blinding �We can apply any succession of blinding factors without affecting the successful decryption c = gm * r 1 n r 2 n. . . rkn mod n 2 = gm * rn mod n 2 7/16/2011 Cliff Mc. Cullough 50

Tallying the Vote �Paillier cryptography is well suited to voting due to its homomorphic property �The multiplication of two ciphertexts is equivalent to the addition of the respective paintexts. (Paillier, 1999, p. 13) �This way, the votes may be tallied without decrypting the ciphertext. 7/16/2011 Cliff Mc. Cullough 51

Homomorphic Paillier �Start with two messages and encrypt c 1 = gm 1 r 1 n mod n 2 c 2 = gm 2 r 2 n mod n 2 �Now multiply the two ciphertexts c 1 * c 2 = gm 1 r 1 n * gm 2 r 2 n mod n 2 = gm 1 gm 2 * r 1 n r 2 n mod n 2 = gm 1 + m 2 * (r 1 r 2)n mod n 2 = gm 3 * r 3 n mod n 2 7/16/2011 Cliff Mc. Cullough 52

References Cited Blinding (cryptography). (2011, June 3). Retrieved July 10, 2011, from Wikipedia: http: //en. wikipedia. org/wiki/Blinding_(cryptography) � Burton, D. M. (2007). Elementary Number Theory, Sixth Edition. New York, New York 10020: Mc. Graw-Hill Higher Education. � Euclidean algorithm. (2011, June 30). Retrieved July 7, 2011, from Wikipedia: http: //en. wikipedia. org/wiki/Euclid_algorithm � Garrett, P. (2004). The Mathematics of Coding Theory. Upper Saddle River, New Jersey: Pearson Prentice Hall. � MPIR home page. (n. d. ). Retrieved July 9, 2011, from MPIR: http: //www. mpir. org/ � Paillier, P. (1999). Public-Key Cryptosystems Based on Composite Degree Residuosity Clases. Advances in Cryptology - Eurocrypt '99 , pp. 223 -238. � 7/16/2011 Cliff Mc. Cullough 53

References continued � Safe prime. (2010, August 24). Retrieved July 9, 2011, from Wikipedia: http: //en. wikipedia. org/wiki/Safe_prime Shamir, A. (November, 1979). How to Share a Secret. Communications of the ACM , 612 -613. � Stallings, W. (2011). Cryptography and Network Security, Principles and Practice, Fifth Edition. Prentice Hall. � The GNU Muliple Precision Arithmetic Library. (n. d. ). Retrieved July 9, 2011, from GNU: http: //gmplib. org/ � 7/16/2011 Cliff Mc. Cullough 54