The Abnormal Distribution Im just misunderstood The Normal

The Abnormal Distribution I’m just misunderstood.

The Normal Distribution • The normal distribution is a very common and useful distribution – Describes many real variables • Height • Weight • IQ • SAT – Can be used to calculate probabilities

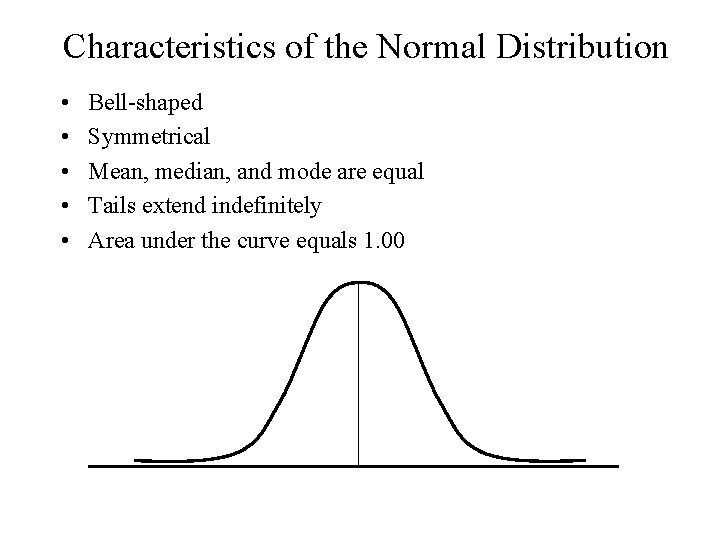
Characteristics of the Normal Distribution • • • Bell-shaped Symmetrical Mean, median, and mode are equal Tails extend indefinitely Area under the curve equals 1. 00

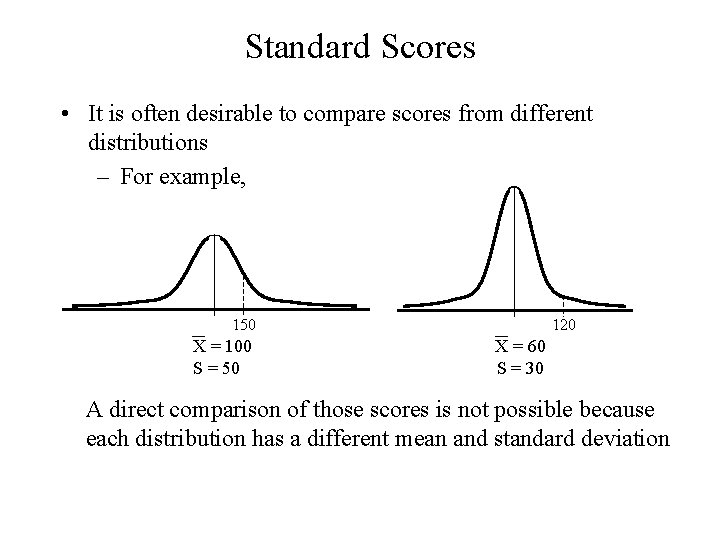
Standard Scores • It is often desirable to compare scores from different distributions – For example, 150 X = 100 S = 50 120 X = 60 S = 30 A direct comparison of those scores is not possible because each distribution has a different mean and standard deviation

Standard Scores • The problem can be solved by converting the original scores to standard scores • Standard scores are scores with a set mean and standard deviation • Examples of standard scores – IQ – t scores – GRE

z Scores • A very useful standard score is the z score • A z score states how many standard deviations the original score is above or below the mean of a distribution 1 s 2 s 150 120 X = 100 S = 50 X = 60 S = 30 X-X z= S

Properties of z Scores • The mean of any set of z scores equals to 0. 0 • The standard deviation of any set of z scores equals 1. 00 • The shape of a distribution of z scores maintains the shape of the original score distribution from which the z scores were derived

Finding Areas Under the Curve • The proportion of area between two scores of a frequency distribution is equal to the proportion of cases between those two scores • The relation between area and proportion permits us to determine probabilities • It is necessary, then, that we be able to determine the area under the curve

The z Score Table • A great deal of the work has been done for us in the z table – Column 1, z – Column 2, Area between mean and z – Column 3, Area beyond z

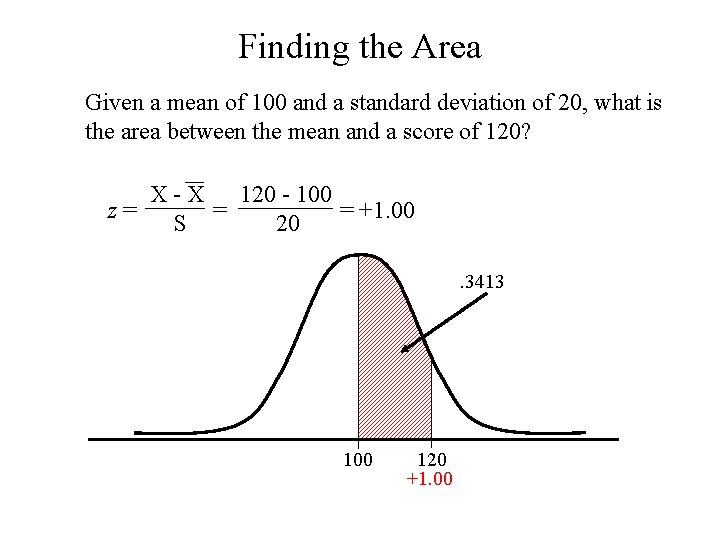
Finding the Area Given a mean of 100 and a standard deviation of 20, what is the area between the mean and a score of 120? X - X 120 - 100 = = +1. 00 z= S 20. 3413 100 120 +1. 00

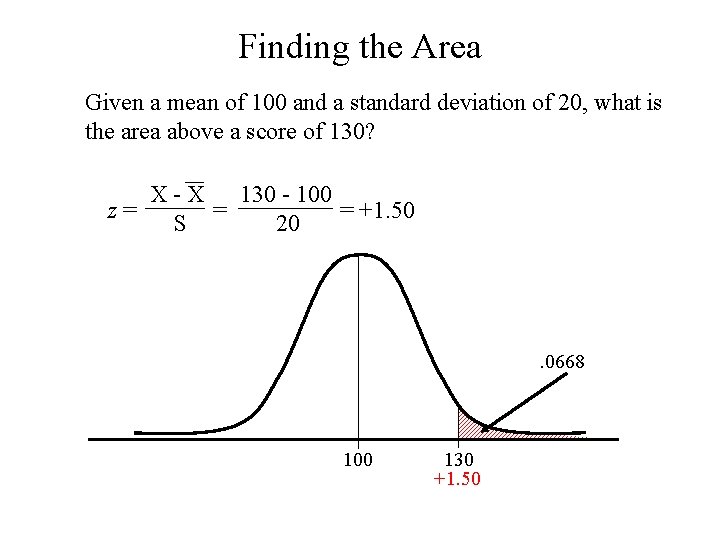
Finding the Area Given a mean of 100 and a standard deviation of 20, what is the area above a score of 130? X - X 130 - 100 = = +1. 50 z= S 20 . 0668 100 130 +1. 50

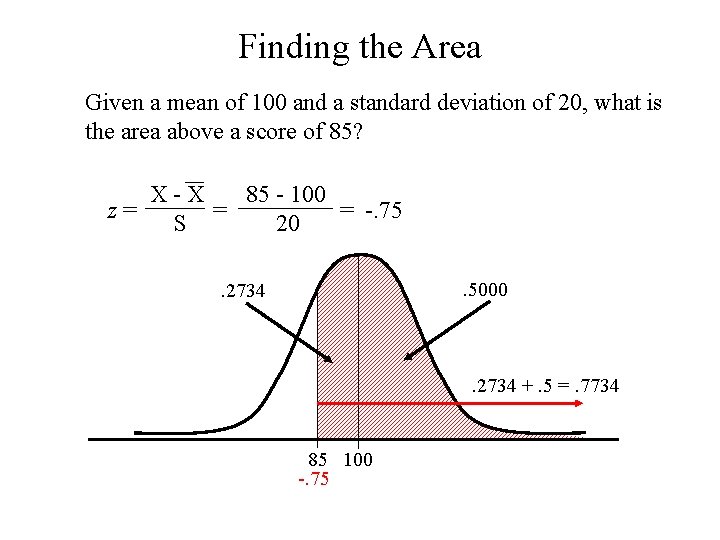
Finding the Area Given a mean of 100 and a standard deviation of 20, what is the area above a score of 85? X-X 85 - 100 = = -. 75 z= S 20. 5000 . 2734 +. 5 =. 7734 85 100 -. 75

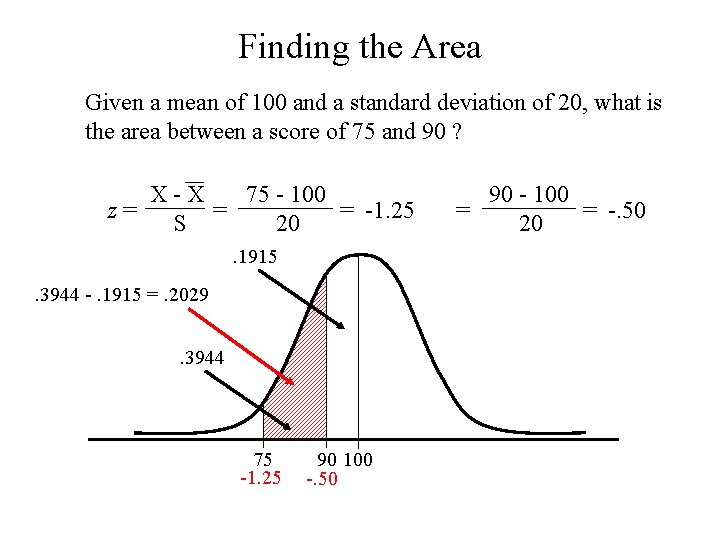
Finding the Area Given a mean of 100 and a standard deviation of 20, what is the area between a score of 75 and 90 ? X-X 75 - 100 = = -1. 25 z= S 20. 1915. 3944 -. 1915 =. 2029. 3944 75 -1. 25 90 100 -. 50 90 - 100 = = -. 50 20

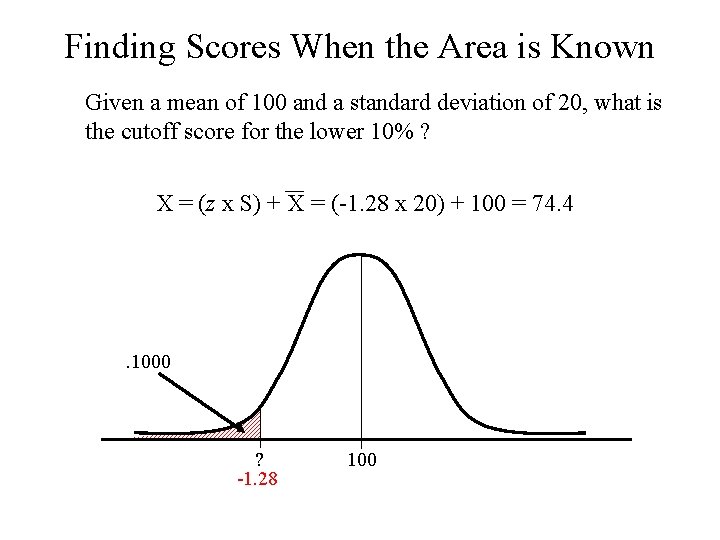
Finding Scores When the Area is Known Given a mean of 100 and a standard deviation of 20, what is the cutoff score for the lower 10% ? X = (z x S) + X = (-1. 28 x 20) + 100 = 74. 4 . 1000 ? -1. 28 100

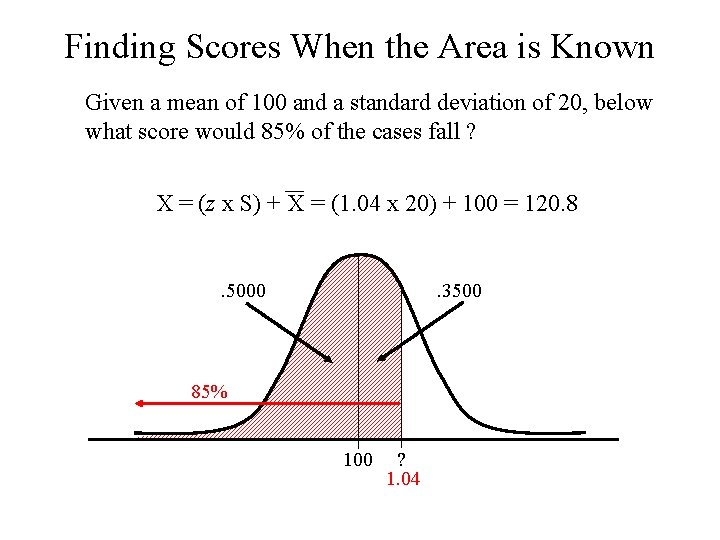
Finding Scores When the Area is Known Given a mean of 100 and a standard deviation of 20, below what score would 85% of the cases fall ? X = (z x S) + X = (1. 04 x 20) + 100 = 120. 8 . 3500 . 5000 85% 100 ? 1. 04