The 3connected property of the pyramid networks YuanHsiang

The 3*-connected property of the pyramid networks Yuan-Hsiang Teng, Tzu-Liang Kung, Lih-Hsing Hsu Computers and Mathematics with Applications 60 (2010) 2360– 2363 1

Abstract o We prove that the pyramid network PM[n] is 3*-connected and super connected for n ≥ 1. 2

Definition and Notation for a Graph o G=(V, E) is a graph if V is a finite set and E is a subset of {(a, b) | (a, b) is an unordered pair of V}. o V is the node set and E is the edge set of G. 3

Hamiltonian Properties o. A hamiltonian path is a path such that its nodes are distinct and span V. o A hamiltonian cycle is a cycle such that its nodes are distinct except for the first node and the last node and span V. o A hamiltonian graph is a graph with a hamiltonian cycle. 4

Connectivity o The connectivity of G, κ(G) is the minimum number of vertices whose removal leaves the remaining graph disconnected or trivial. 5

Container o. A k-container C(u, v) in a graph G is a set of k disjoint paths joining u to v. o A k*-container C(u, v) in a graph G is a kcontainer such that every vertex of G is on some path in C(u, v). 6

k*-connected o o o A graph G is k*-connected if there exists a k*container between any two distinct vertices in G. A graph G is 1*-connected if and only if it is hamiltonian connected. A graph G is 2*-connected if it is hamiltonian. The study of k*-connected graph is motivated by the 3*-connected graphs proposed by Albert et al. M. Albert, E. R. L. Aldred, D. Holton, J. Sheehan, On 3*-connected graphs, Australasian Journal of Combinatorics 24 (2001) 193 -207. 7

Super connected o A graph G is super connected if it is i*connected for all 1≤ i ≤ κ(G). • H. C. Hsu, C. K. Lin, H. M. Huang, L. H. Hsu, The spanning connectivity of the (n, k)star graphs, International Journal of Foundations of Computer Science 17 (2006) 415– 434. • C. K. Lin, H. M. Huang, L. H. Hsu, The super connectivity of the pancake graphs and the super laceability of the star graphs, Theoretical Computer Science 339 (2005) 257– 271. 8

Introduction o o o κ(PM[n])=3 Sarbazi-Azad et al. and. Wu et al. studied the hamiltonicity and the hamiltonian connectivity of the pyramid networks. Thus the pyramid network is 1*-connected and 2*connected. H. Sarbazi-Azad, H. M. Ould-Khaoua, L. M. Mackenzie, Algorithmic construction of hamiltonians in pyramids, Information Processing Letters 80 (2001) 75 -79. R. Y. Wu, D. R. Duh, Hamiltonicity of the pyramid network with or without fault, Journal fo Information Science and Engineering 25 (2009) 531 -542. 9

Introduction o o o In this paper, we study the 3*-connected property of the pyramid network. We prove that any pyramid network is 3*connected. Moreover, the pyramid network is super connected. 10

The pyramid networks o o o An n-dimensional pyramid network PM[n] is a hierarchy structure based on mesh networks. The subgraph induced by all vertices in the ith layer of a PM[n] is a mesh network M(2 i, 2 i). V (PM[n]) = {(k; x; y) | 0 ≤k ≤ n; 1 ≤ x ≤ 2 k; 1 ≤y ≤ 2 k}. 11

The pyramid networks o Two vertices (k 1; x 1; y 1) and (k 2; x 2; y 2) in PM[n] are adjacent if they satisfy one of the following conditions: 12

The pyramid networks PM[2] 13

Lemma 1 o A pyramid network PM[n] is hamiltonian for n ≥ 1. • H. Sarbazi-Azad, H. M. Ould-Khaoua, L. M. Mackenzie, Algorithmic construction of Hamiltonians in pyramids, Information Processing Letters 80 (2001) 75– 79. • R. Y. Wu, D. R. Duh, Hamiltonicity of the pyramid network with or without fault, Journal of Information Science and Engineering 25 (2009) 531– 542. 14

Lemma 2 o A pyramid network PM[n] is hamiltonian connected for n ≥ 1. R. Y. Wu, D. R. Duh, Hamiltonicity of the pyramid network with or without fault, Journal of Information Science and Engineering 25 (2009) 531– 542. 15

Lemma 3 o A pyramid network PM[n] with one vertex fault is hamiltonian for n ≥ 1. R. Y. Wu, D. R. Duh, Hamiltonicity of the pyramid network with or without fault, Journal of Information Science and Engineering 25 (2009) 531– 542. 16

Lemma 4 o A mesh network M(m, n) is hamiltonian laceable except : (1) m = 2 and n ≠ 2, and (2) m = 3 and n = 2 m. G. Simmons, Almost all n-dimensional rectangular lattices are Hamiltonian laceable, Congressus Numerantium (1978) 103– 108. 17

Lemma 5 o A mesh network M(m, n) is hamiltonian for m = n. 18

Theorem 1 o o o Assume that n ≥ 1. Let s and t be any two distinct vertices of a pyramid network PM[n]. Then there exists a 3*-container C 3*(s, t) of PM[n]. 19

Proof of Theorem 1 o o o We prove this theorem by induction. By brute force, we check theorem holds for n = 1. Assume theorem holds for any PM[n-1] with n > 1. 20

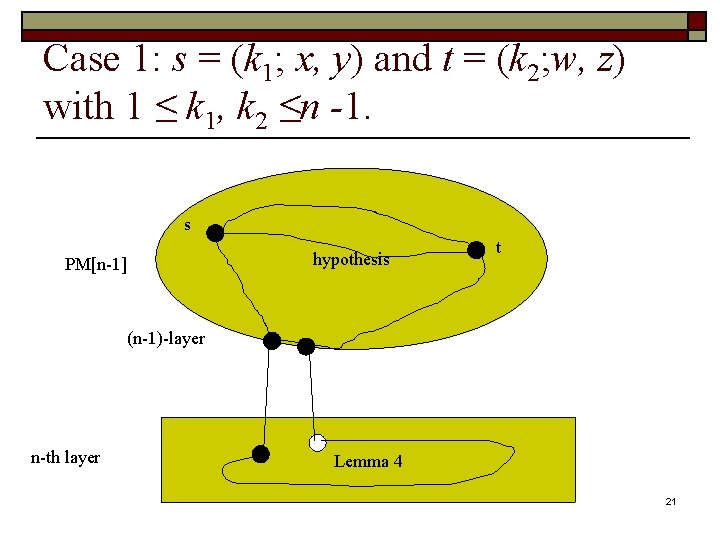
Case 1: s = (k 1; x, y) and t = (k 2; w, z) with 1 ≤ k 1, k 2 ≤n -1. s hypothesis PM[n-1] t (n-1)-layer n-th layer Lemma 4 21

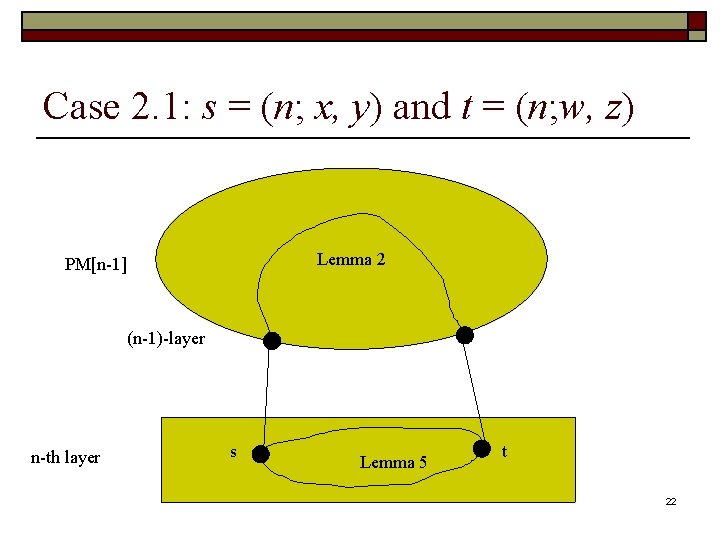
Case 2. 1: s = (n; x, y) and t = (n; w, z) Lemma 2 PM[n-1] (n-1)-layer n-th layer s Lemma 5 t 22

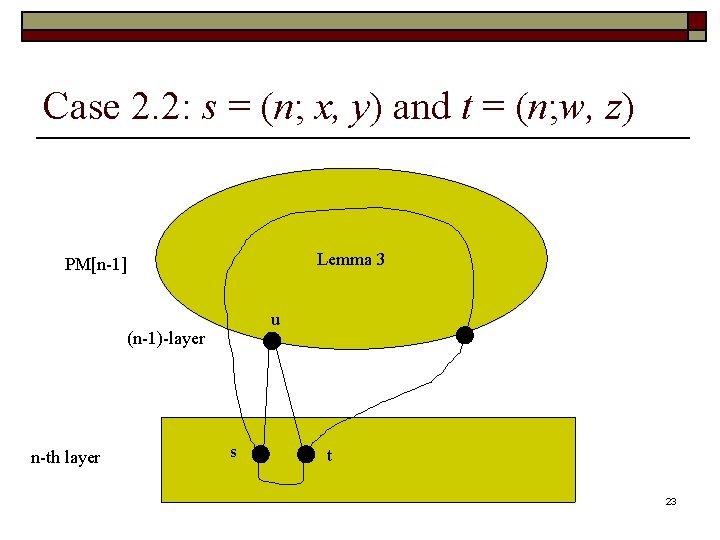
Case 2. 2: s = (n; x, y) and t = (n; w, z) Lemma 3 PM[n-1] u (n-1)-layer n-th layer s t 23

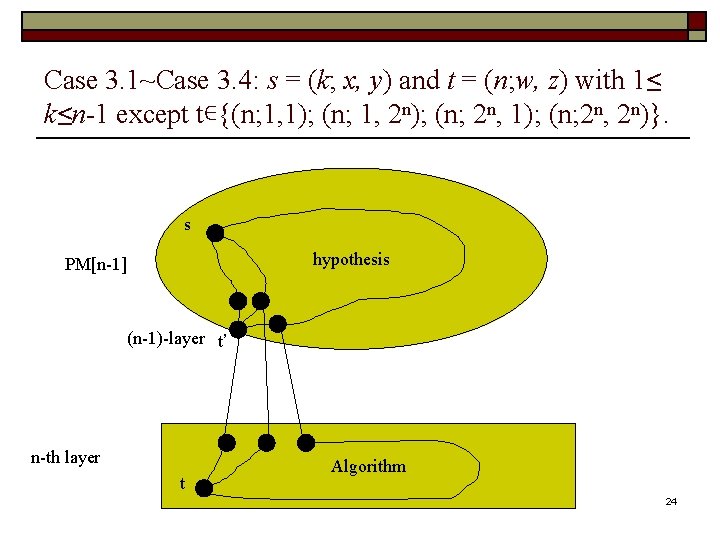
Case 3. 1~Case 3. 4: s = (k; x, y) and t = (n; w, z) with 1≤ k≤n-1 except t∊{(n; 1, 1); (n; 1, 2 n); (n; 2 n, 1); (n; 2 n, 2 n)}. s hypothesis PM[n-1] (n-1)-layer t’ n-th layer t Algorithm 24

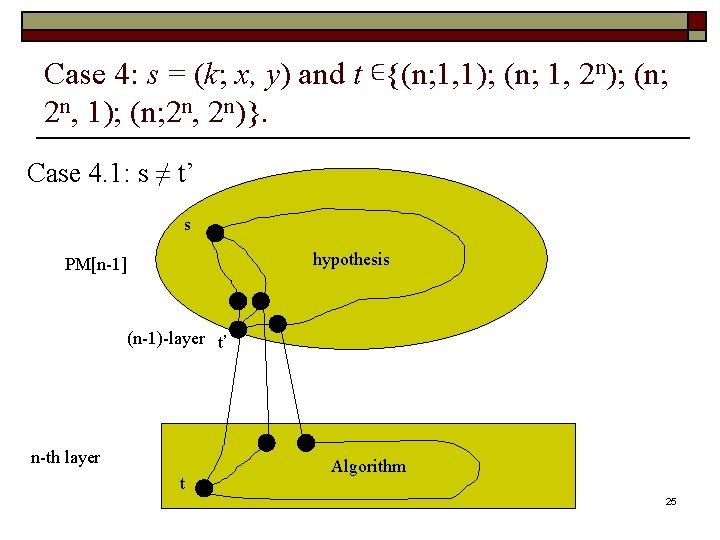
Case 4: s = (k; x, y) and t ∊{(n; 1, 1); (n; 1, 2 n); (n; 2 n, 1); (n; 2 n, 2 n)}. Case 4. 1: s ≠ t’ s hypothesis PM[n-1] (n-1)-layer t’ n-th layer t Algorithm 25

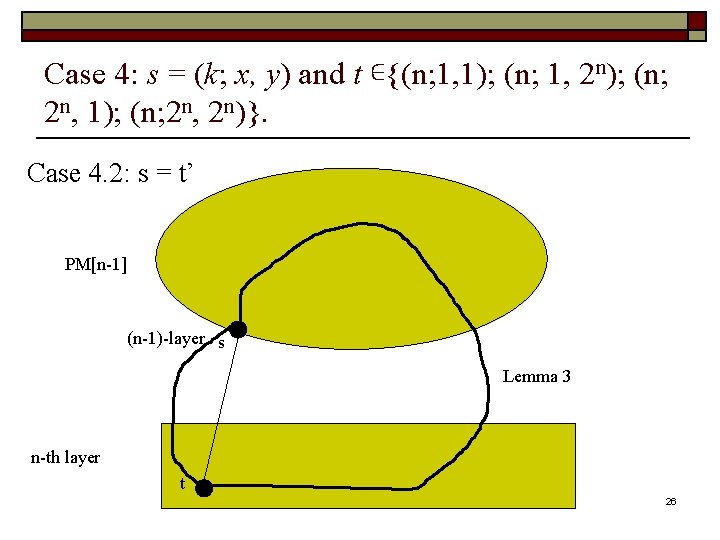
Case 4: s = (k; x, y) and t ∊{(n; 1, 1); (n; 1, 2 n); (n; 2 n, 1); (n; 2 n, 2 n)}. Case 4. 2: s = t’ PM[n-1] (n-1)-layer s Lemma 3 n-th layer t 26

Corollary 1 o o The pyramid network PM[n] is super connected for n ≥ 1. By Lemma 1, Lemma 2, and Theorem 1, the pyramid network is k*-connected for 1 ≤k ≤ 3. 27