Texture Arbitrary Illumination n Vary a surface property

Texture = Arbitrary Illumination n Vary a surface property non-linearly n n Rasterization does bi-linear interpolation Examples of usage: n Paste a picture n picture of environment n picture of scene n Modify surface normals n Create bumps and detail

Texture Mapping n Texture aka function of a surface n n f (x, y, z) = some attribute value Would like f to be arbitrary n n Look-up table is a possible implementation n No continuity constraints But not all x, y, z has the surface through it Surface is only a 2 -manifold 2 D look-up table n n But want to map every point on a surface to a 2 D space <u, v> parameterization
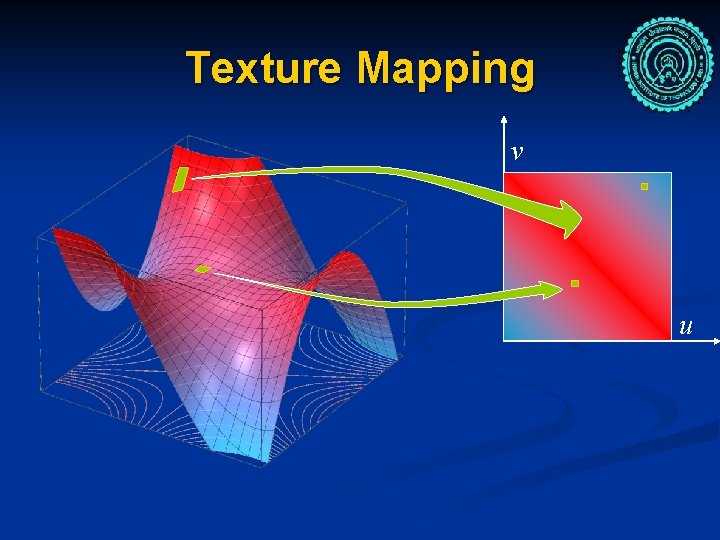
Texture Mapping v u
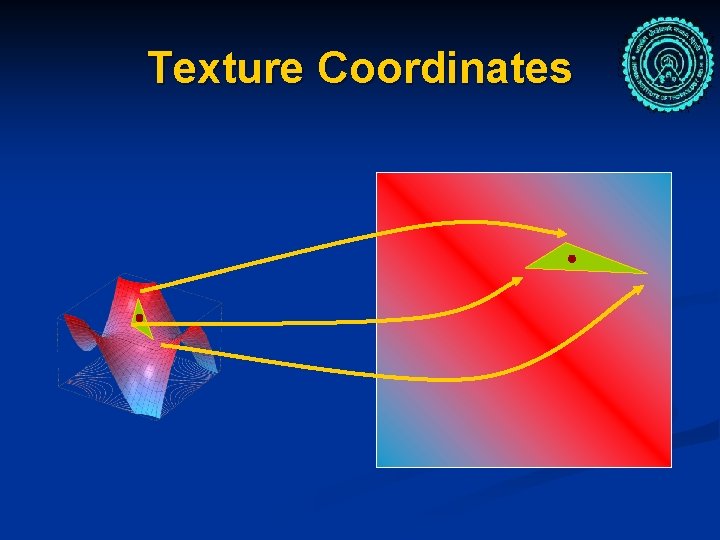
Texture Coordinates
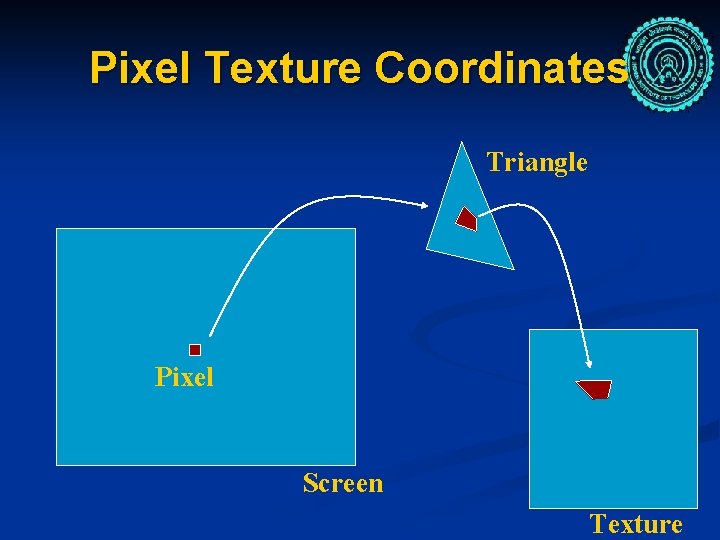
Pixel Texture Coordinates Triangle Pixel Screen Texture
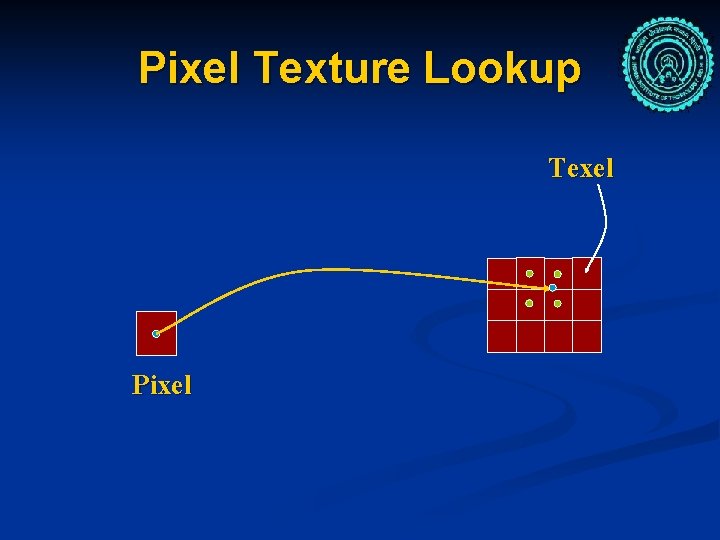
Pixel Texture Lookup Texel Pixel
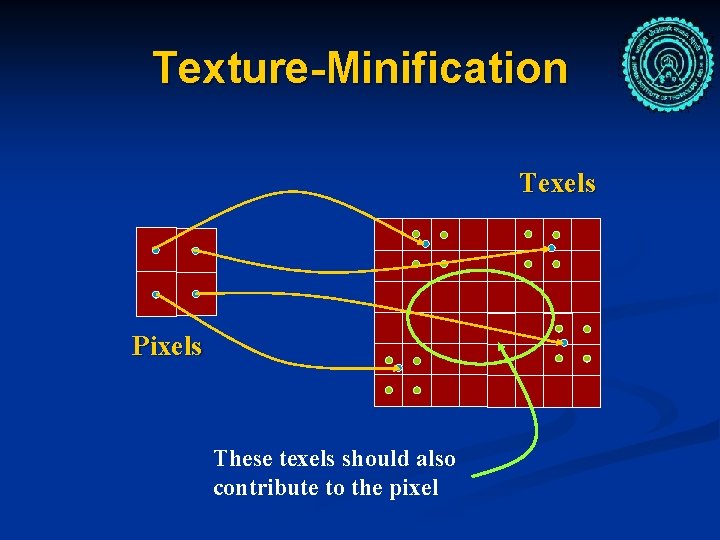
Texture-Minification Texels Pixels These texels should also contribute to the pixel
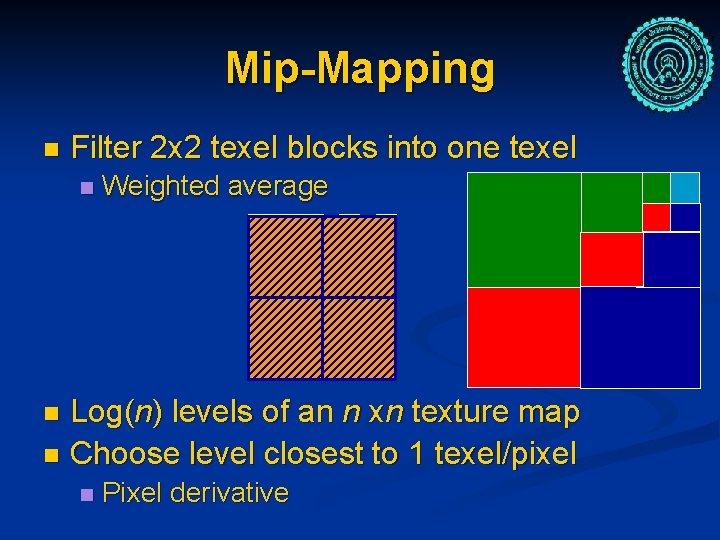
Mip-Mapping n Filter 2 x 2 texel blocks into one texel n Weighted average Log(n) levels of an n xn texture map n Choose level closest to 1 texel/pixel n n Pixel derivative

Derivative Tex coord: t 0 t-1 t 2 Pixels Texels t 1 t 3 t 1 – t 0 = (∆t xu, ∆t vx ) t 2 – t 0 = ( ∆t yu , ∆t yv) ∆t = Wx. H texture => texel size = 1/W x 1/H max (∆txu , ∆tyu), max(∆txu , ∆tyv) Use divided difference: t 1 – t-1

Anisotropic Filter Texels Pixels Use Smallest minification May read several texels
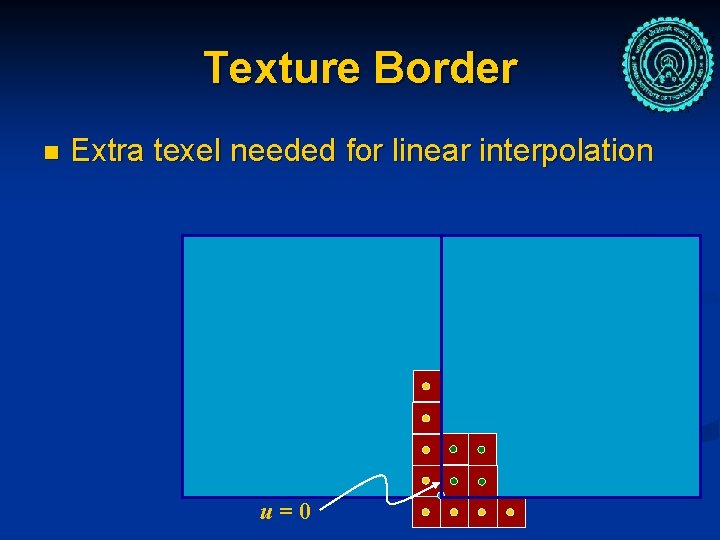
Texture Border n Extra texel needed for linear interpolation u=0

Other Texture Usage n Alpha Map n n Transparent texture Light Map n n Diffused lighting independent of viewer How do you generate it? n n n Texel to Object space reverse-mapping Specular Map Displacement Map Bump Map Environment Map Point Sprites

Point Sprites n Draw points n E. g. , as a k x k pixel square Map a (small) texture on the point n Typically used with transparency n For example a cursor n

Bump Mapping
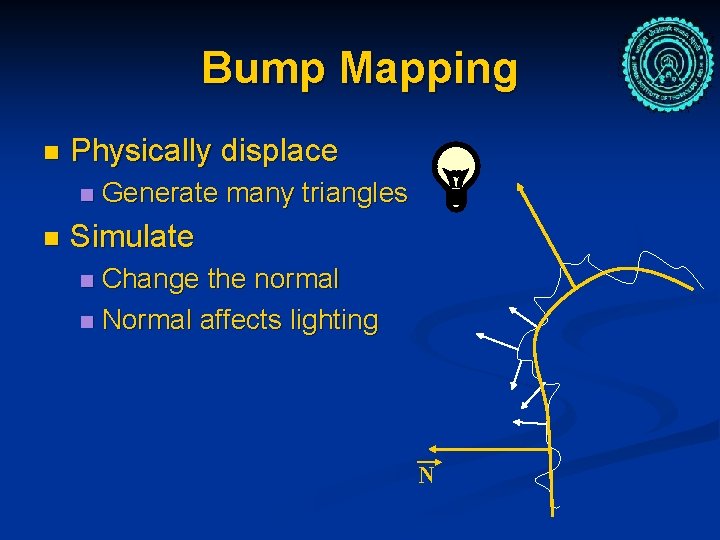
Bump Mapping n Physically displace n n Generate many triangles Simulate Change the normal n Normal affects lighting n N

Bump Mapping n Assume ‘Bump’ to the surface is small n In the direction of the normal n aka Height-map n n Simulation: P' = P + B(u, v) N P'(u, v) = P(u, v) + B(u, v) N(u, v)

Bump Mapping n n Tangent to the surface P(u, v) at a point (u, v): P u, P v N The normal is then: n N(u, v) n = Pu Pv P'(u, v) = P(u, v) + B(u, v) N n n P'u = Pu + Bu N + B Nu P'u = Pu + Bu N P'v = Pv + Bv N + B Nv P'v = Pv + Bv N (if B is small) n P'u x P'v = Pu Pv + Bu(N Pv) - Bv(N Pu) + Bu Bv(N N)
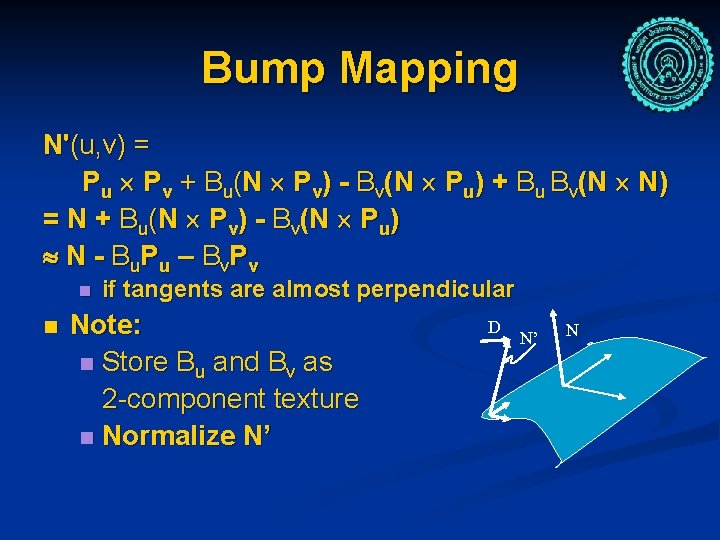
Bump Mapping N'(u, v) = Pu Pv + Bu(N Pv) - Bv(N Pu) + Bu Bv(N N) = N + B u ( N P v ) - B v( N P u ) N - B u P u – B v. P v n n if tangents are almost perpendicular Note: n Store Bu and Bv as 2 -component texture n Normalize N’ D N’ N

Normal Mapping Directly store the new normal per texel n From bump map: n Nx = (0, 1, Bu) n Ny = (1, 0, Bv) n N = Nx X Ny n Remember to normalize n n (and range compress)

Displacement Mapping n Modifies the surface position n n Along surface normal, typically Use if Bumps are large Get silhouettes, shadows right Much more expensive n n Tessellate geometry Some support in modern GPUs
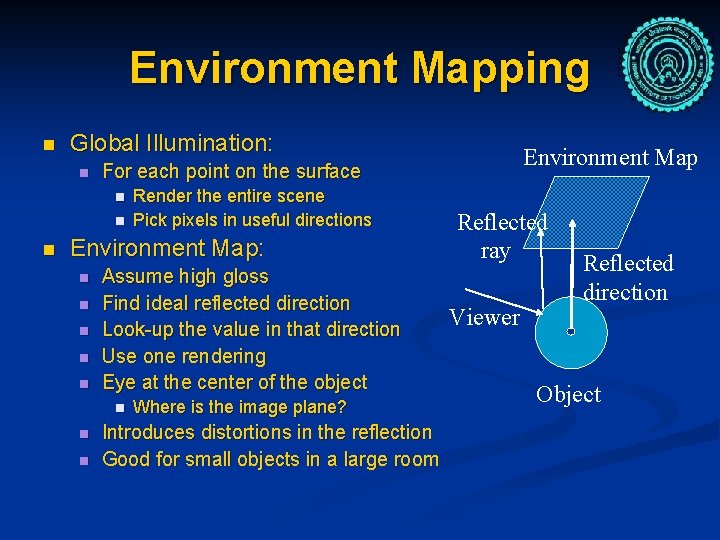
Environment Mapping n Global Illumination: n n Render the entire scene Pick pixels in useful directions Environment Map: n n n Assume high gloss Find ideal reflected direction Look-up the value in that direction Use one rendering Eye at the center of the object n n n Environment Map For each point on the surface Where is the image plane? Introduces distortions in the reflection Good for small objects in a large room Reflected ray Viewer Reflected direction Object

Example

Cube Mapping n Map onto surfaces of a cube (around the object) n n n Find desired direction from a surface point Cube map accessed by the direction n Axis-aligned often One of the six faces of the cube intersects The corresponding texture is looked up For environment mapping: n Render scene from object-center onto cube face n n Use, e. g, the six axis-aligned directions Rendering may be pre-computed at high quality n E. g. , 6 photos of a real environment

Cube Map Example
- Slides: 24