Text Independent Speaker Identification Using Gaussian Mixture Model

Text Independent Speaker Identification Using Gaussian Mixture Model Chee-Ming Ting Sh-Hussain Salleh Tian-Swee Tan A. K. Ariff. International Conference on Intelligent and Advanced Systems 2007 Jain-De, Lee

OUTLINE � INTRODUCTION � GMM SPEAKER IDENTIFICATION SYSTEM � EXPERIMENTAL EVALUATION � CONCLUSION

INTRODUCTION � Speaker recognition is generally divided into two tasks ◦ Speaker Verification(SV) ◦ Speaker Identification(SI) � Speaker model ◦ Text-dependent(TD) ◦ Text-independent(TI)

INTRODUCTION � Many approaches have been proposed for TI speaker recognition ◦ VQ based method ◦ Hidden Markov Models ◦ Gaussian Mixture Model � VQ based method

INTRODUCTION � Hidden Markov Models ◦ State Probability ◦ Transition Probability � Classify acoustic events corresponding to HMM states to characterize each speaker in TI task � TI performance is unaffected by discarding transition probabilities in HMM models

INTRODUCTION � Gaussian Mixture Model ◦ Corresponds to a single state continuous ergodic HMM ◦ Discarding the transition probabilities in the HMM models � The use of GMM for speaker identity modeling ◦ The Gaussian components represent some general speakerdependent spectral shapes ◦ The capability of Gaussian mixture to model arbitrary densities

GMM SPEAKER IDENTIFICATION SYSTEM � The GMM speaker identification system consists of the following elements ◦ Speech processing ◦ Gaussian mixture model ◦ Parameter estimation ◦ Identification

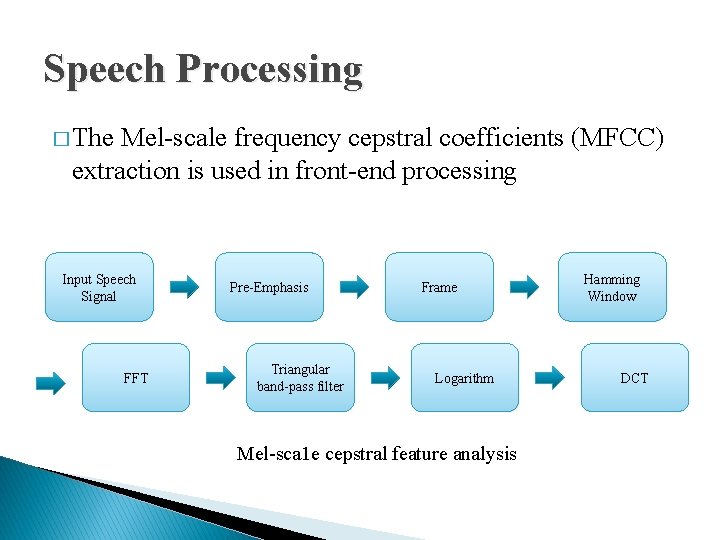
Speech Processing � The Mel-scale frequency cepstral coefficients (MFCC) extraction is used in front-end processing Input Speech Signal FFT Pre-Emphasis Triangular band-pass filter Frame Logarithm Mel-sca 1 e cepstral feature analysis Hamming Window DCT

Gaussian mixture model � The Gaussian model is a weighted linear combination of M uni-model Gaussian component densities Where is a D-dimensional vector are the component densities wi , i=1, …, M are the mixture weights � The mixture weight satisfy the constraint that

Gaussian mixture model � Each component density is a D-variate Gaussian function of the form Where is mean vector is covariance matrix � The Gaussian mixture density model are denoted as

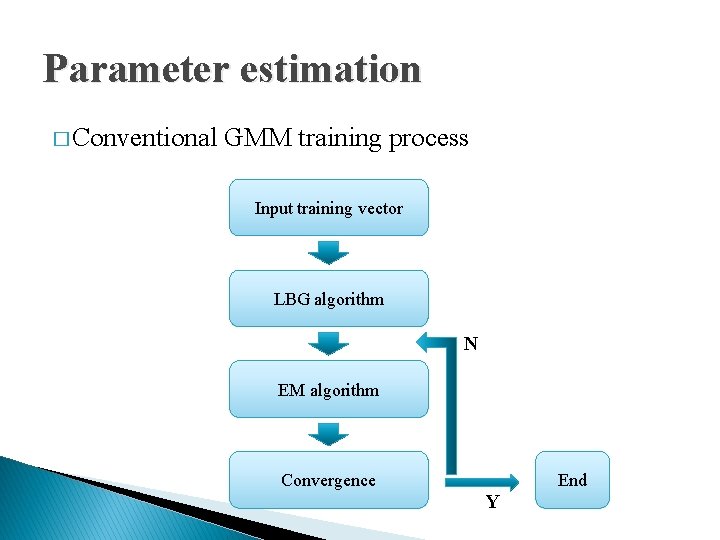
Parameter estimation � Conventional GMM training process Input training vector LBG algorithm N EM algorithm Convergence End Y

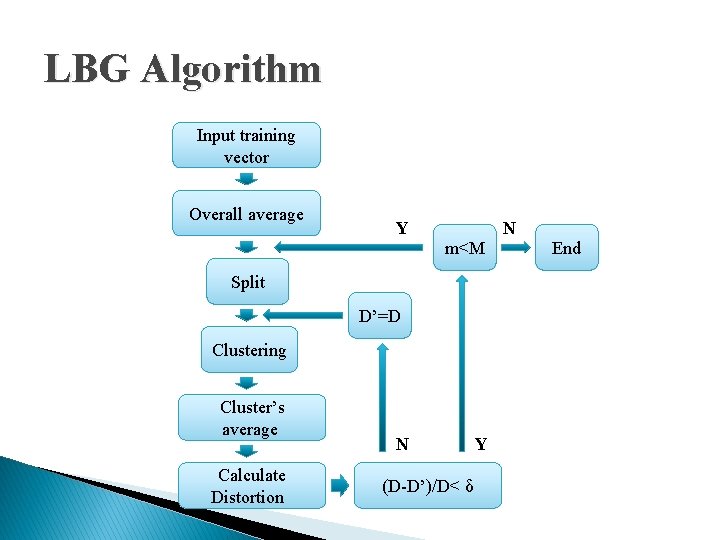
LBG Algorithm Input training vector Overall average Y N m<M Split D’=D Clustering Cluster’s average Calculate Distortion N (D-D’)/D< δ Y End

EM Algorithm � Speaker model training is to estimate the GMM parameters via maximum likelihood (ML) estimation � Expectation-maximization (EM) algorithm

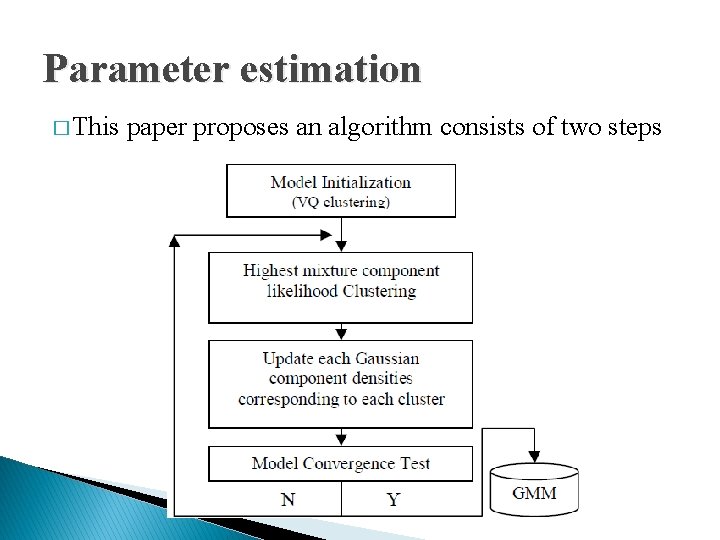
Parameter estimation � This paper proposes an algorithm consists of two steps

Parameter estimation � Cluster the training vectors to the mixture component with the highest likelihood � Re-estimate parameters of each component number of vectors classified in cluster i / total number of training vectors sample mean of vectors classified in cluster i. sample covariance matrix of vectors classified in cluster i

Identification � The feature is classified to the speaker , whose likelihood is the highest � The above can be formulated in logarithmic term model

EXPERIMENTAL EVALUATION � Database and Experiment Conditions ◦ 7 male and 3 female ◦ The same 40 sentences utterances with different text ◦ The average sentences duration is approximately 3. 5 s � Performance Comparison between EM and Highest Mixture Likelihood Clustering Training ◦ The number of Gaussian components 16 ◦ 16 dimensional MFCCs ◦ 20 utterances is used for training

EXPERIMENTAL EVALUATION � Convergence condition

EXPERIMENTAL EVALUATION � The comparison between EM and highest likelihood clustering training on identification rate ◦ ◦ 10 sentences were used for training 25 sentences were used for testing 4 Gaussian components 8 iterations

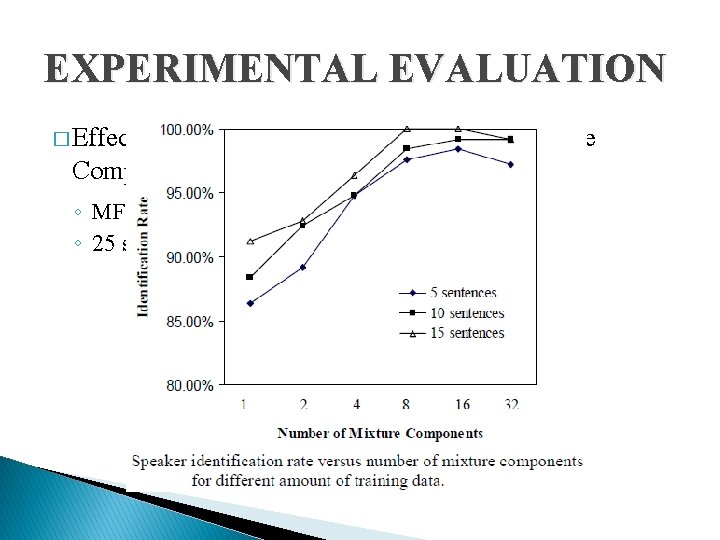
EXPERIMENTAL EVALUATION � Effect of Different Number of Gaussian Mixture Components and Amount of Training Data ◦ MFCCs feature dimension is fixed to 12 ◦ 25 sentences is used for testing

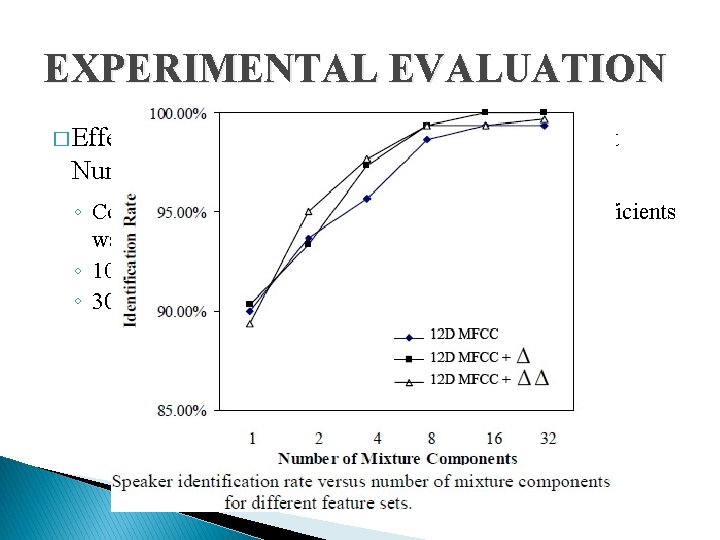
EXPERIMENTAL EVALUATION � Effect of Feature Set on Performance for Different Number of Gaussian Mixture Components ◦ Combination with first and second order difference coefficients was tested ◦ 10 sentences is used for training ◦ 30 sentences is used for testing

CONCLUSION � Comparably to conventional EM training but with less computational time � First order difference coefficients is sufficient to capture the transitional information with reasonable dimensional complexity � The 12 dimensional 16 order GMM and using 5 training sentences achieved 98. 4% identification rate