Tests About a Population Proportion LEARNING TARGETS By

Tests About a Population Proportion LEARNING TARGETS By the end of this section, you should be able to: üSTATE and CHECK the Random, 10%, and Large Counts conditions for performing a significance test about a population proportion. üCALCULATE the standardized test statistic and P-value for a test about a population proportion. üPERFORM a significance test about a population proportion. Starnes/Tabor, The Practice of Statistics

Performing a Significance Test About p Conditions for Performing a Significance Test About a Proportion • Random: The data come from a random sample from the population of interest. o 10%: When sampling without replacement, n < 0. 10 N. • Large Counts: Both np 0 and n(1 – p 0) are at least 10. Because we assume H 0 is true when performing a significance test, we use the parameter value specified by the null hypothesis (denoted p 0) when checking the Large Counts condition. Starnes/Tabor, The Practice of Statistics

Performing a Significance Test About p Problem: According to the U. S. Census Bureau, the Art. Well/Shutterstock. com proportion of students in high school who have a part-time job is 0. 25. An administrator at a local high school suspects that the proportion of students at her school who have a part-time job is less than the national figure. She would like to carry out a test at the α = 0. 05 significance level of H 0: p = 0. 25 Ha: p < 0. 25 where p = the true proportion of all students at the school who have a part-time job. The administrator selects a random sample of 200 students from the school and finds that 39 of them have a part-time job. Check if the conditions for performing the significance test are met. Starnes/Tabor, The Practice of Statistics

Performing a Significance Test About p Problem: She would like to carry out a test at the α = 0. 05 significance level of H 0: p = 0. 25 Ha: p < 0. 25 where p = the true proportion of all students at the school who have a part-time job. The administrator selects a random sample of 200 students from the school and finds that 39 of them have a part-time job. Check if the conditions for performing the significance test are met. • Random? Random sample of 200 students from the school. ✓ º 10%: 200 is less than 10% of students at a large high school. ✓ • Large Counts? np 0 = 200(0. 25) = 50 ≥ 10 and n(1 – p 0) = 200(1 – 0. 25) = 150 ≥ 10 ✓ Starnes/Tabor, The Practice of Statistics

Performing a Significance Test About p A basketball player claims to be an 80% free-throw H : p = 0. 25 0 shooter. You think the player is exaggerating. Ha: p < 0. 25 Starnes/Tabor, The Practice of Statistics

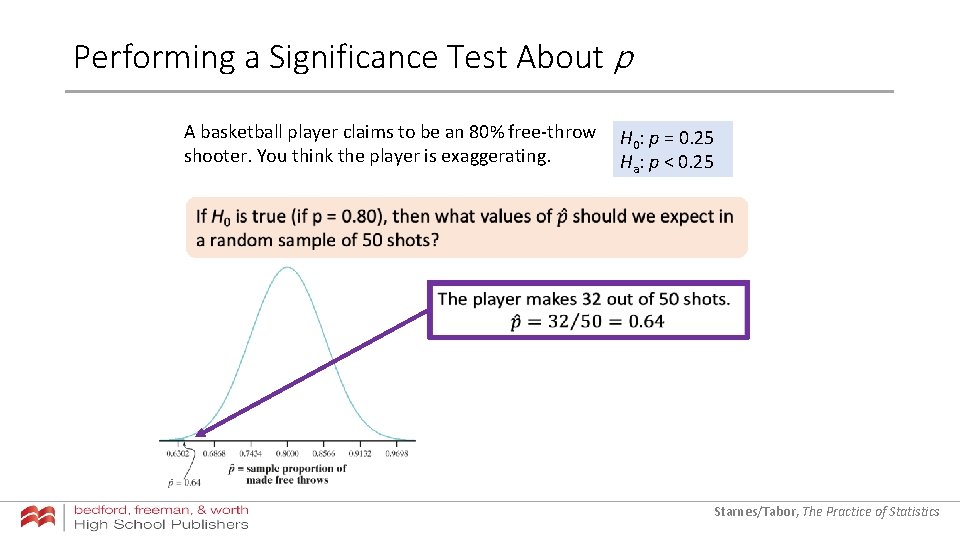
Performing a Significance Test About p A basketball player claims to be an 80% free-throw H : p = 0. 25 0 shooter. You think the player is exaggerating. Ha: p < 0. 25 The value z = – 2. 83 is called the standardized test statistic. Starnes/Tabor, The Practice of Statistics

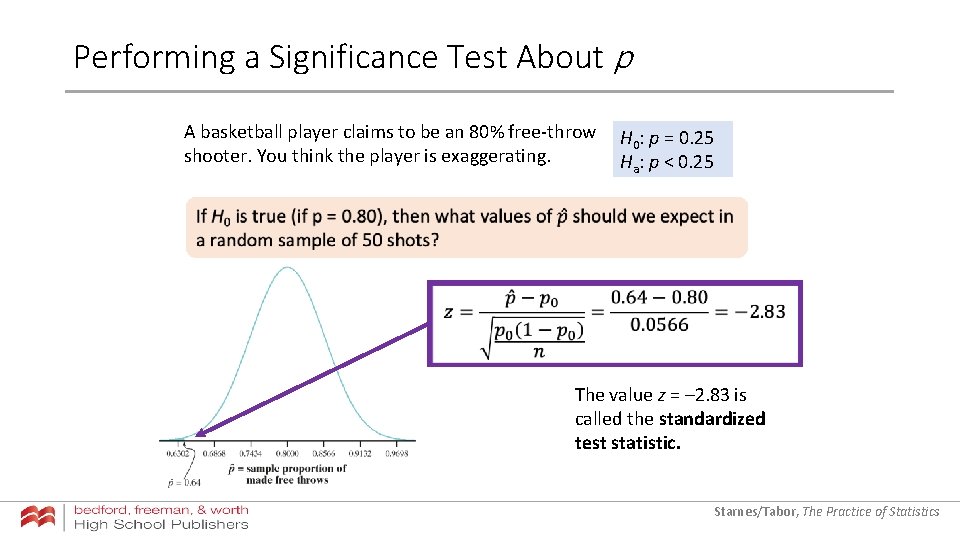
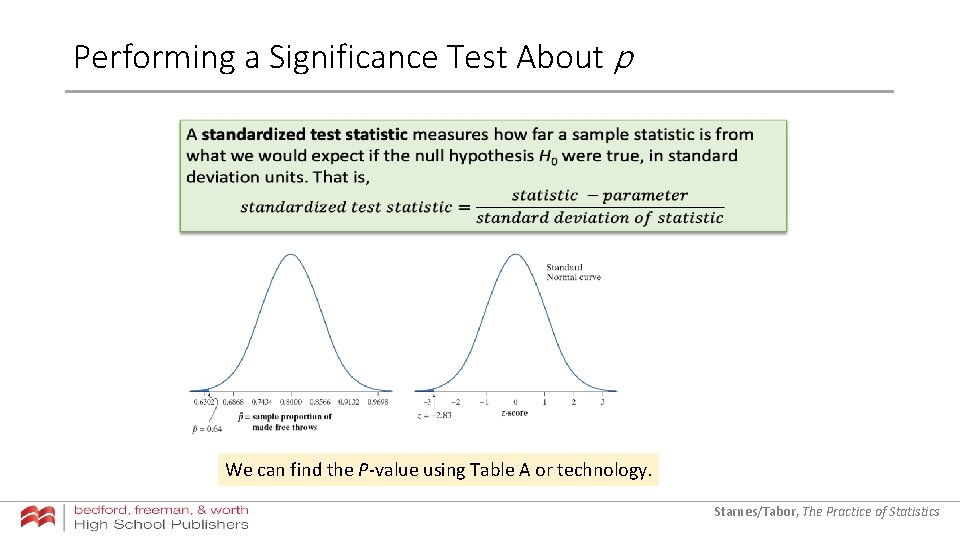
Performing a Significance Test About p We can find the P-value using Table A or technology. Starnes/Tabor, The Practice of Statistics

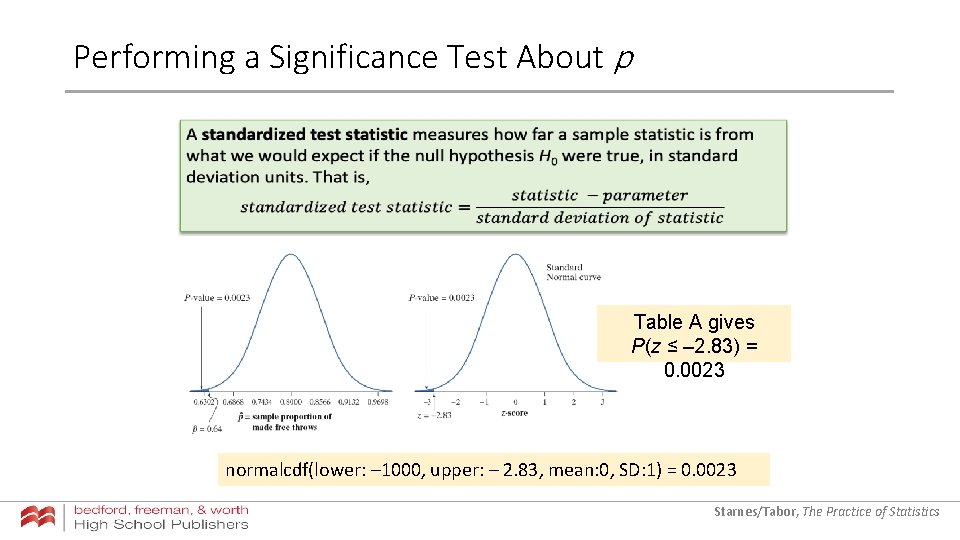
Performing a Significance Test About p Table A gives P(z ≤ – 2. 83) = 0. 0023 normalcdf(lower: – 1000, upper: – 2. 83, mean: 0, SD: 1) = 0. 0023 Starnes/Tabor, The Practice of Statistics

Performing a Significance Test About p local high school decided to perform a test at the α = 0. 05 significance level of H 0: p = 0. 25 Ha: p < 0. 25 where p = the true proportion of all students at the school who have a part-time job. The administrator selects a random sample of 200 students from the school and finds that 39 of them have a part-time job. We already confirmed that the conditions for performing a significance test are met. (a) Explain why the sample result gives some evidence for the alternative hypothesis. (b) Calculate the standardized test statistic and P-value. (c) What conclusion would you make? Andersen Ross/Exactostock-1555/Superstock Problem: In the preceding example, an administrator at a Starnes/Tabor, The Practice of Statistics

Problem: H 0: p = 0. 25 Ha: p < 0. 25 The administrator selects a random sample of 200 students from the school and finds that 39 of them have a part-time job. (a) Explain why the sample result gives some evidence for the alternative hypothesis. Andersen Ross/Exactostock-1555/Superstock Performing a Significance Test About p Starnes/Tabor, The Practice of Statistics

Problem: H 0: p = 0. 25 Ha: p < 0. 25 The administrator selects a random sample of 200 students from the school and finds that 39 of them have a part-time job. (b) Calculate the standardized test statistic and P-value. Andersen Ross/Exactostock-1555/Superstock Performing a Significance Test About p Starnes/Tabor, The Practice of Statistics

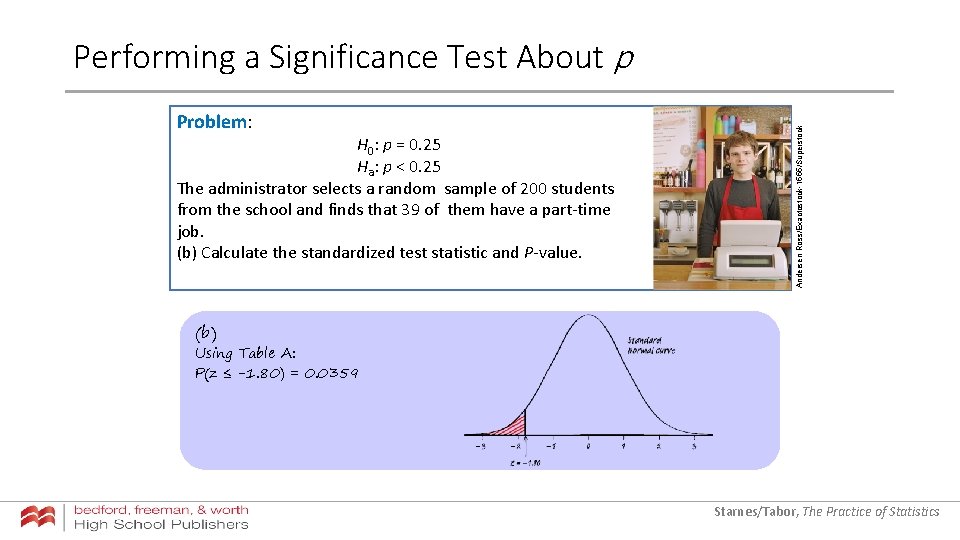
Problem: H 0: p = 0. 25 Ha: p < 0. 25 The administrator selects a random sample of 200 students from the school and finds that 39 of them have a part-time job. (b) Calculate the standardized test statistic and P-value. Andersen Ross/Exactostock-1555/Superstock Performing a Significance Test About p (b) Using Table A: P(z ≤ -1. 80) = 0. 0359 Starnes/Tabor, The Practice of Statistics

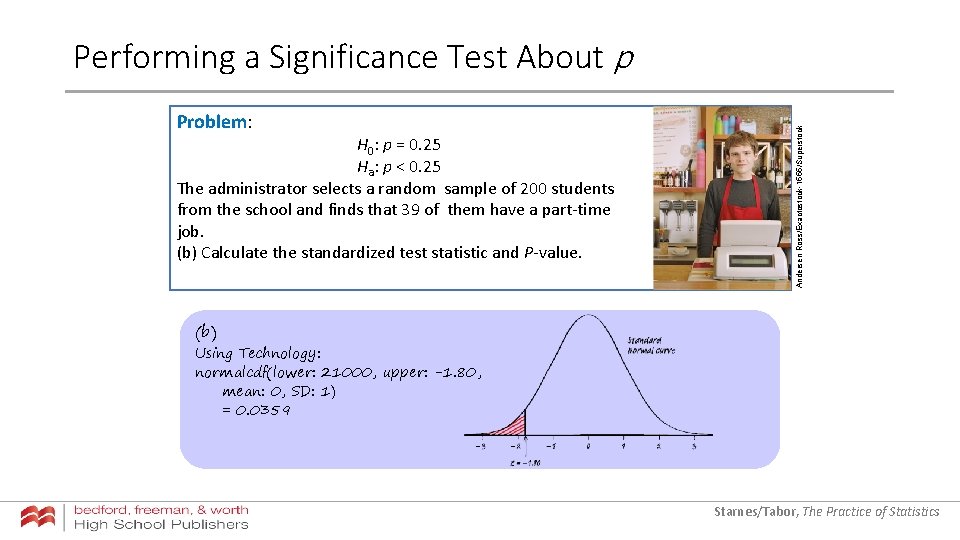
Problem: H 0: p = 0. 25 Ha: p < 0. 25 The administrator selects a random sample of 200 students from the school and finds that 39 of them have a part-time job. (b) Calculate the standardized test statistic and P-value. Andersen Ross/Exactostock-1555/Superstock Performing a Significance Test About p (b) Using Technology: normalcdf(lower: 21000, upper: -1. 80, mean: 0, SD: 1) = 0. 0359 Starnes/Tabor, The Practice of Statistics

Performing a Significance Test About p Andersen Ross/Exactostock-1555/Superstock Problem: H 0: p = 0. 25 Ha: p < 0. 25 The administrator selects a random sample of 200 students from the school and finds that 39 of them have a part-time job. (c) What conclusion would you make? (c) Because the P-value of 0. 0359 < α = 0. 05, we reject H 0. We have convincing evidence that the true proportion of all students at this large high school who have a part-time job is less than 0. 25. Starnes/Tabor, The Practice of Statistics

Putting It All Together: One-Sample z Test for p Significance Tests: A Four-Step Process State: State the hypotheses you want to test and the significance level, and define any parameters you use. Plan: Identify the appropriate inference method and check conditions. Do: If the conditions are met, perform calculations. • Give the sample statistic(s). • Calculate the standardized test statistic. • Find the P-value. Conclude: Make a conclusion about the hypotheses in the context of the problem. Starnes/Tabor, The Practice of Statistics

Putting It All Together: One-Sample z Test for p There are three conditions that must be met for the formula for the standardized test statistic to be valid—one for each of the three components in the formula. Starnes/Tabor, The Practice of Statistics

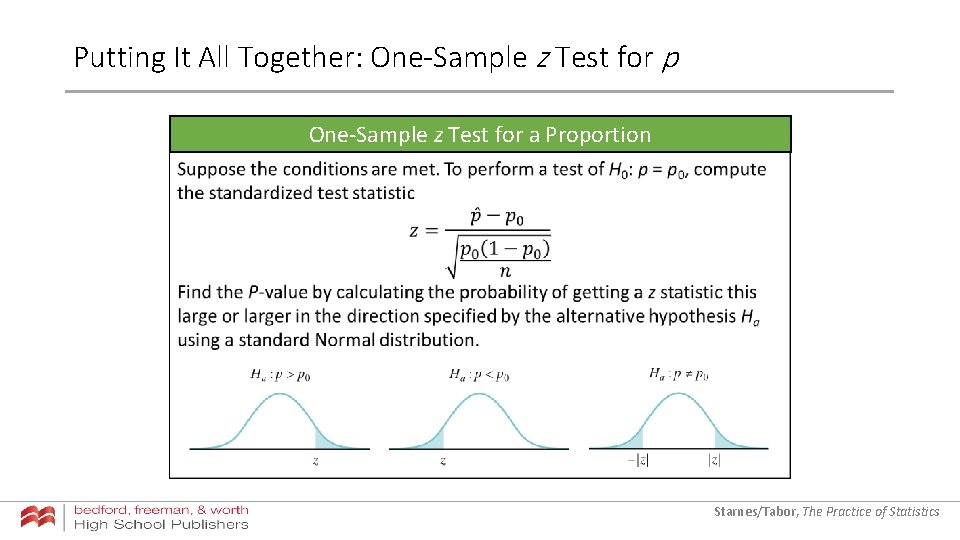
Putting It All Together: One-Sample z Test for p One-Sample z Test for a Proportion Starnes/Tabor, The Practice of Statistics

Putting It All Together: One-Sample z Test for p Section 9. 1 and its main supplier agree that each shipment of potatoes must meet certain quality standards. If the producer finds convincing evidence that more than 8% of the potatoes in the shipment have “blemishes, ” the truck will be sent away to get another load of potatoes from the supplier. Otherwise, the entire truckload will be used to make potato chips. The potato-chip producer has just received a truckload of potatoes from the supplier. A supervisor selects a random sample of 500 potatoes from the truck. An inspection reveals that 47 of the potatoes have blemishes. Is there convincing evidence at the α = 0. 10 level that more than 8% of the potatoes in the shipment have blemishes? imagestock/Getty Images Problem: Recall that the potato-chip producer we met in Starnes/Tabor, The Practice of Statistics

Putting It All Together: One-Sample z Test for p 500 potatoes from the truck. An inspection reveals that 47 of the potatoes have blemishes. Is there convincing evidence at the α = 0. 10 level that more than 8% of the potatoes in the shipment have blemishes? imagestock/Getty Images Problem: A supervisor selects a random sample of STATE: We want to test H 0: p = 0. 08 Ha: p > 0. 08 where p = the true proportion of potatoes in this shipment with blemishes, using α = 0. 10. Starnes/Tabor, The Practice of Statistics

Putting It All Together: One-Sample z Test for p Problem: A supervisor selects a random sample of imagestock/Getty Images 500 potatoes from the truck. An inspection reveals that 47 of the potatoes have blemishes. Is there convincing evidence at the α = 0. 10 level that more than 8% of the potatoes in the shipment have blemishes? PLAN: One-sample z test for p • Random: Random sample of 500 potatoes from the shipment. ✓ º 10%: It’s reasonable to assume that 500 * 10% of all potatoes in the shipment. ✓ • Large Counts: 500(0. 08) = 40 ≥ 10 and 500(0. 92) = 460 ≥ 10 ✓ Starnes/Tabor, The Practice of Statistics

Putting It All Together: One-Sample z Test for p Problem: A supervisor selects a random sample of imagestock/Getty Images 500 potatoes from the truck. An inspection reveals that 47 of the potatoes have blemishes. Is there convincing evidence at the α = 0. 10 level that more than 8% of the potatoes in the shipment have blemishes? P-value: Using Table A: P(z ≥ 1. 15) = 1 – 0. 8749 = 0. 1251 Using technology: normalcdf(lower: 1. 15, upper: 1000, mean: 0, SD: 1) = 0. 1251 Starnes/Tabor, The Practice of Statistics

Putting It All Together: One-Sample z Test for p Problem: A supervisor selects a random sample of imagestock/Getty Images 500 potatoes from the truck. An inspection reveals that 47 of the potatoes have blemishes. Is there convincing evidence at the α = 0. 10 level that more than 8% of the potatoes in the shipment have blemishes? CONCLUDE: Because our P-value of 0. 1251 > α = 0. 10, we fail to reject H 0. There is not convincing evidence that the true proportion of blemished potatoes in the shipment is greater than 0. 08. Starnes/Tabor, The Practice of Statistics

Putting It All Together: One-Sample z Test for p AP® Exam Tip When a significance test leads to a fail to reject H 0 decision, as in the preceding example, be sure to interpret the results as “We don’t have convincing evidence for Ha. ” Saying anything that sounds like you believe H 0 is (or might be) true will lead to a loss of credit. For instance, it would be wrong to conclude, “There is convincing evidence that the true proportion of blemished potatoes is 0. 08. ” And don’t write responses as text messages, like “FTR the H 0. ” Starnes/Tabor, The Practice of Statistics

Putting It All Together: One-Sample z Test for p AP® Exam Tip You can use your calculator to carry out the mechanics of a significance test on the AP® Statistics exam. But there’s a risk involved. If you give just the calculator answer with no work, and one or more of your values are incorrect, you will probably get no credit for the “Do” step. If you opt for the calculator-only method, be sure to name the procedure (one -sample z test for a proportion) and to report the standardized test statistic (z = 1. 15) and P-value (0. 1243). Starnes/Tabor, The Practice of Statistics

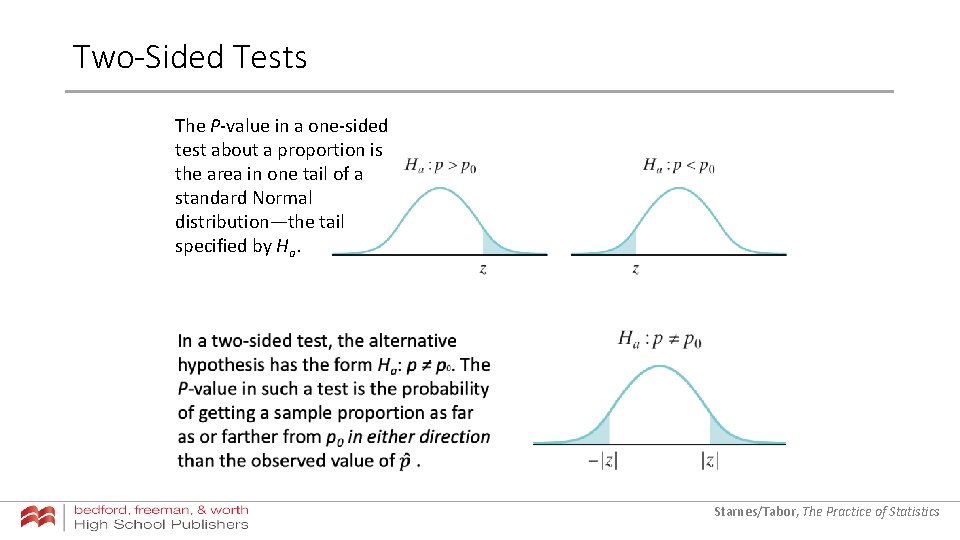
Two-Sided Tests The P-value in a one-sided test about a proportion is the area in one tail of a standard Normal distribution—the tail specified by Ha. Starnes/Tabor, The Practice of Statistics

Two-Sided Tests and Prevention (CDC) website, 68% of high school students have never smoked a cigarette. Yanhong wonders whether this national result holds true in her large, urban high school. For her AP® Statistics class project, Yanhong surveys a simple random sample of 150 students from her school. She gets responses from all 150 students, and 90 say that they have never smoked a cigarette. Is there convincing evidence that the CDC’s claim does not hold true at Yanhong’s school? snowmeo/Getty Images Problem: According to the Centers for Disease Control Starnes/Tabor, The Practice of Statistics

Two-Sided Tests Problem: According to the Centers for Disease Control snowmeo/Getty Images and Prevention (CDC) website, 68% of high school students have never smoked a cigarette. Yanhong wonders whether this national result holds true in her large, urban high school. For her AP® Statistics class project, Yanhong surveys a simple random sample of 150 students from her school. She gets responses from all 150 students, and 90 say that they have never smoked a cigarette. Is there convincing evidence that the CDC’s claim does not hold true at Yanhong’s school? STATE: We want to test H 0: p = 0. 68 Ha: p ≠ 0. 68 where p = the proportion of all students in Yanhong’s school who would say they have never smoked a cigarette. We’ll use α = 0. 05. Starnes/Tabor, The Practice of Statistics

Two-Sided Tests Problem: According to the Centers for Disease Control snowmeo/Getty Images and Prevention (CDC) website, 68% of high school students have never smoked a cigarette. Yanhong wonders whether this national result holds true in her large, urban high school. For her AP® Statistics class project, Yanhong surveys a simple random sample of 150 students from her school. She gets responses from all 150 students, and 90 say that they have never smoked a cigarette. Is there convincing evidence that the CDC’s claim does not hold true at Yanhong’s school? PLAN: One-sample z test for p. • Random: Yanhong surveyed an SRS of 150 students. ✓ º 10%: 150 students is less than 10% of all students at her large urban school. ✓ • Large Counts: 150(0. 68) = 102 ≥ 10 and 150(0. 32) = 48 ≥ 10 ✓ Starnes/Tabor, The Practice of Statistics

Two-Sided Tests and Prevention (CDC) website, 68% of high school students have never smoked a cigarette. Yanhong wonders whether this national result holds true in her large, urban high school. For her AP® Statistics class project, Yanhong surveys a simple random sample of 150 students from her school. She gets responses from all 150 students, and 90 say that they have never smoked a cigarette. Is there convincing evidence that the CDC’s claim does not hold true at Yanhong’s school? snowmeo/Getty Images Problem: According to the Centers for Disease Control Starnes/Tabor, The Practice of Statistics

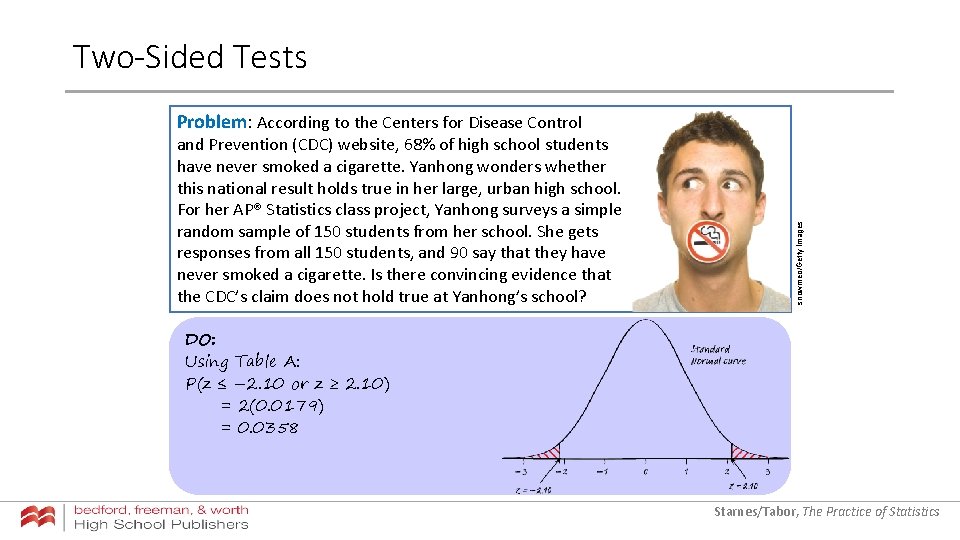
Two-Sided Tests and Prevention (CDC) website, 68% of high school students have never smoked a cigarette. Yanhong wonders whether this national result holds true in her large, urban high school. For her AP® Statistics class project, Yanhong surveys a simple random sample of 150 students from her school. She gets responses from all 150 students, and 90 say that they have never smoked a cigarette. Is there convincing evidence that the CDC’s claim does not hold true at Yanhong’s school? snowmeo/Getty Images Problem: According to the Centers for Disease Control DO: Using Table A: P(z ≤ – 2. 10 or z ≥ 2. 10) = 2(0. 0179) = 0. 0358 Starnes/Tabor, The Practice of Statistics

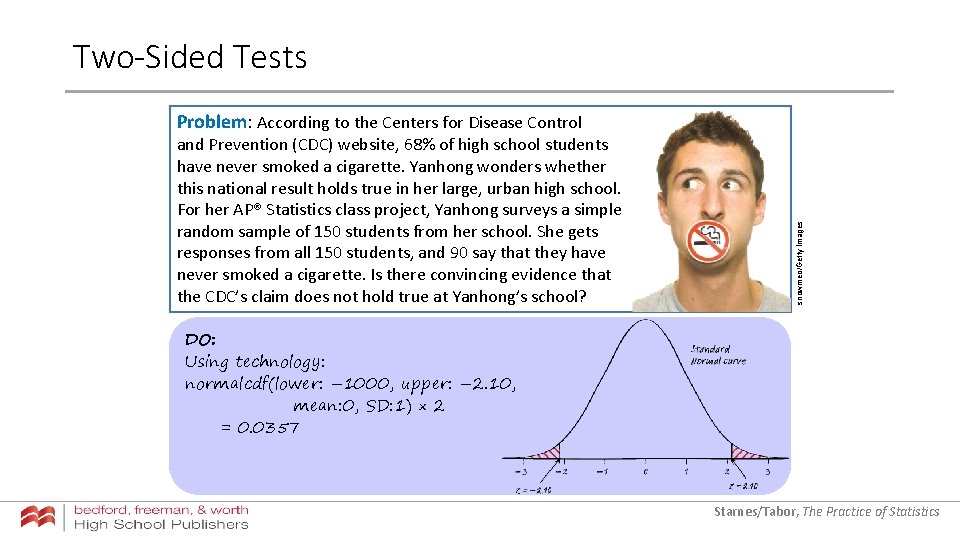
Two-Sided Tests and Prevention (CDC) website, 68% of high school students have never smoked a cigarette. Yanhong wonders whether this national result holds true in her large, urban high school. For her AP® Statistics class project, Yanhong surveys a simple random sample of 150 students from her school. She gets responses from all 150 students, and 90 say that they have never smoked a cigarette. Is there convincing evidence that the CDC’s claim does not hold true at Yanhong’s school? snowmeo/Getty Images Problem: According to the Centers for Disease Control DO: Using technology: normalcdf(lower: – 1000, upper: – 2. 10, mean: 0, SD: 1) × 2 = 0. 0357 Starnes/Tabor, The Practice of Statistics

Two-Sided Tests Problem: According to the Centers for Disease Control snowmeo/Getty Images and Prevention (CDC) website, 68% of high school students have never smoked a cigarette. Yanhong wonders whether this national result holds true in her large, urban high school. For her AP® Statistics class project, Yanhong surveys a simple random sample of 150 students from her school. She gets responses from all 150 students, and 90 say that they have never smoked a cigarette. Is there convincing evidence that the CDC’s claim does not hold true at Yanhong’s school? CONCLUDE: Because our P-value of 0. 0357 < α = 0. 05, we reject H 0. We have convincing evidence that the proportion of all students at Yanhong’s school who would say they have never smoked a cigarette differs from the CDC’s claim of 0. 68. Starnes/Tabor, The Practice of Statistics

Two-Sided Tests AP® Exam Tip When making a conclusion in a significance test, be sure that you are describing the parameter and not the statistic. In the preceding example, it’s wrong to say that we have convincing evidence that the proportion of students at Yanhong’s school who said they have never smoked differs from the CDC’s claim of 0. 68. The “proportion who said they have never smoked” is the sample proportion, which is known to be 0. 60. The test gives convincing evidence that the proportion of all students at Yanhong’s school who would say they have never smoked a cigarette differs from 0. 68. Starnes/Tabor, The Practice of Statistics