Testing the BoseEinstein Condensate dark matter model with

Testing the Bose-Einstein Condensate dark matter model with galactic rotation curves from the SPARC sample

Content • • 1. Bose-Einstein condensation 2. Dark matter as a Bose-Einstein condensate 3. The SPARC sample 4. Testing Bose-Einstein Condensate dark matter model • 5. Conclusions

1. Bose-Einstein condensation • At very low temperatures, all particles in a dilute Bose gas condense to the same quantum ground state, forming a BEC, i. e. , a sharp peak over a broader distribution in both coordinates and momentum space. • Particles become correlated with each other when their wavelengths overlap, that is, thermal wavelength is greater than the mean inter-particles distance • This happens at a temperature
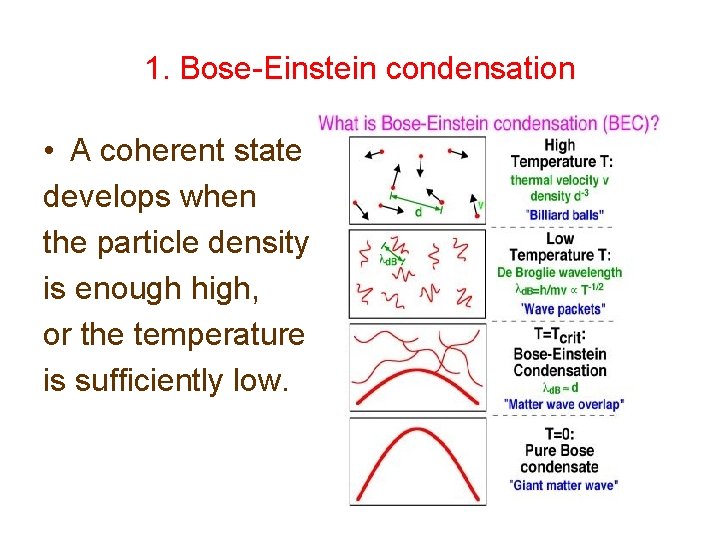
1. Bose-Einstein condensation • A coherent state develops when the particle density is enough high, or the temperature is sufficiently low.
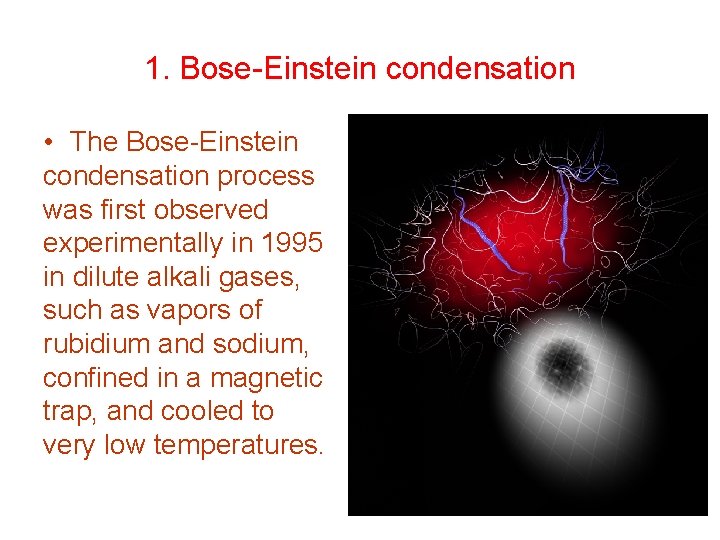
1. Bose-Einstein condensation • The Bose-Einstein condensation process was first observed experimentally in 1995 in dilute alkali gases, such as vapors of rubidium and sodium, confined in a magnetic trap, and cooled to very low temperatures.

1. Bose-Einstein condensation A sharp peak in the velocity distribution was observed below a critical temperature, indicating that condensation has occurred. The alkali atoms are condensed in the same ground state.

1. Bose-Einstein condensation • In the second quantization approach the Hamiltonian describing a many body system of interacting bosons In the Heisenberg representation the field operator is

1. Bose-Einstein condensation • The equation of motion is

1. Bose-Einstein condensation • The equation describing the Bose-Einstein condensate is the Schrodinger equation (Gross-Pitaevski equation) for the condensate wave function with a quartic non-linear term a is the coherent scattering length, the zero-energy limit of the scattering amplitude f

1. Bose-Einstein condensation Basic equations of Bose-Einstein condensates in the hydrodynamical representation

2. Dark matter as a Bose-Einstein condensate Cosmological observations reveal the remarkable phenomenon that 95% of the mass-energy of the Universe resides in two forms that we call dark matter and dark energy
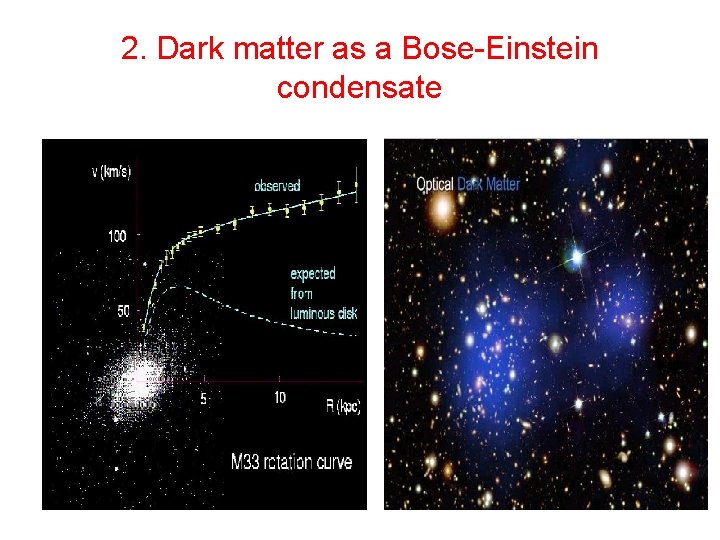
2. Dark matter as a Bose-Einstein condensate

2. Dark matter as a Bose-Einstein condensate Dark matter is thought to be composed by cold neutral weakly interacting massive elementary particles, beyond those existing in the Standard Model, and not yet detected in accelerators, or in dedicated direct and indirect searches.
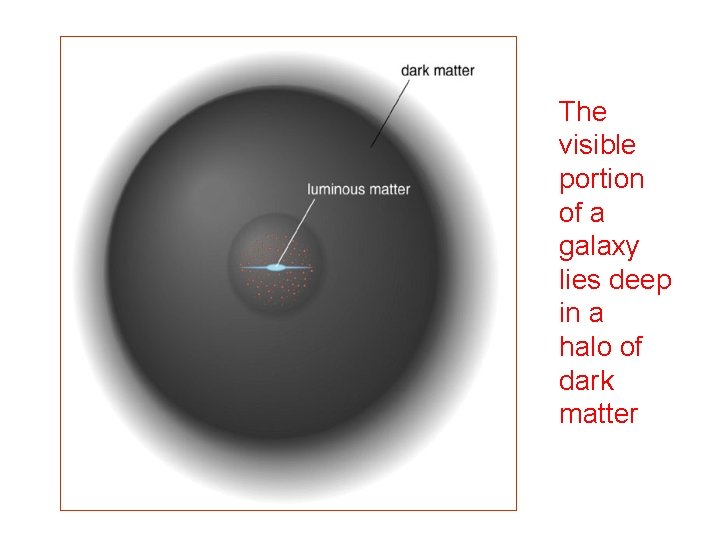
The visible portion of a galaxy lies deep in a halo of dark matter

What is Dark Matter? ==> Neutral and Stable Particle/s • The SM has no suitable candidates: • leptons, hadrons: too little photons: • neutrinos: too light W/Z bosons: not stable • Most suitable candidates beyond the Standard Model: • Axions • Weakly interacting particles (WIMPS) with masses and interaction cross sections of order of the electroweak scale WIMP prototypes: LSP ==> lightest SUSY particle, neutralino, with R-parity conservation. LKP ==> Extra dimensional KK U(1) gauge boson w/ KK parity conserved. LTP ==> T-odd heavy photon in Little Higgs models w/ T-parity conserved.

2. Dark matter as a Bose-Einstein condensate •

2. Dark matter as a Bose-Einstein condensate •

2. Dark matter as a Bose-Einstein condensate -Static condensate

2. Dark matter as a Bose-Einstein condensate

2. Dark matter as a Bose-Einstein condensate

2. Dark matter as a Bose-Einstein condensate •

2. Dark matter as a Bose-Einstein condensate •

3. The SPARC sample •
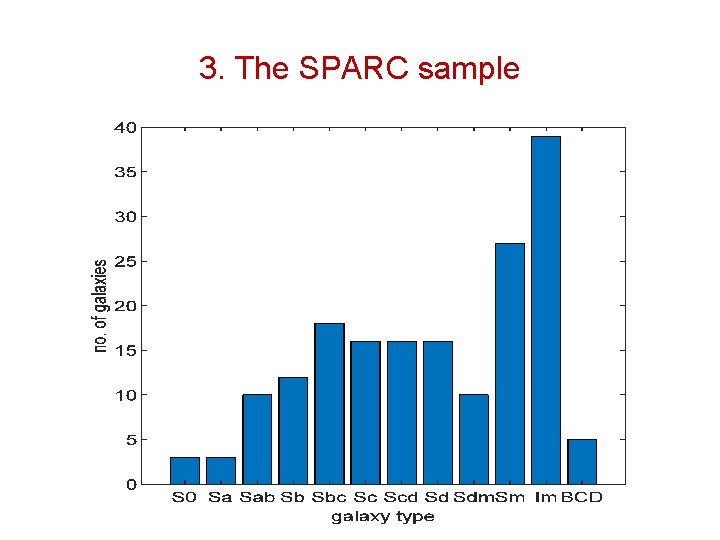
3. The SPARC sample
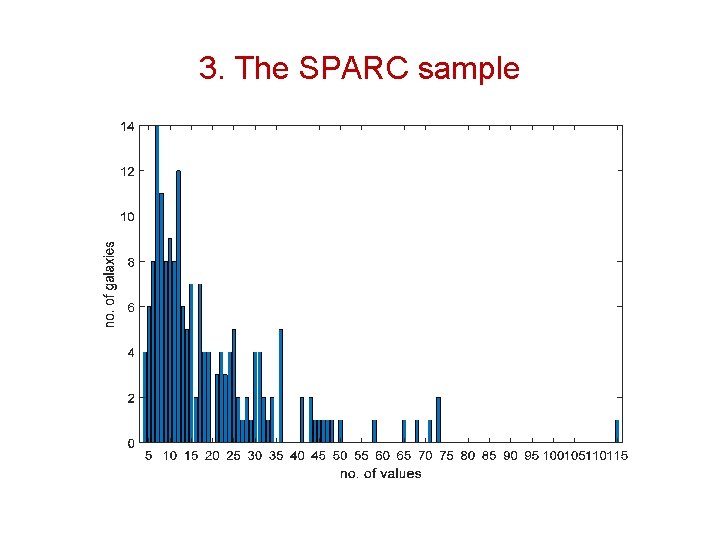
3. The SPARC sample

3. The SPARC sample •

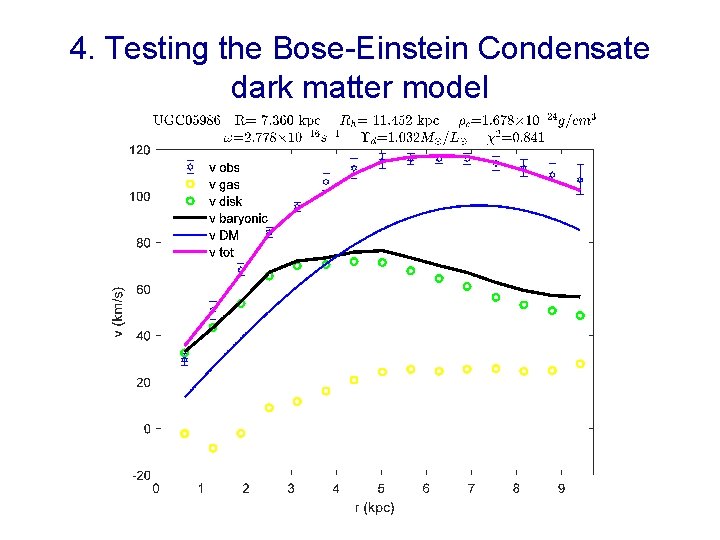
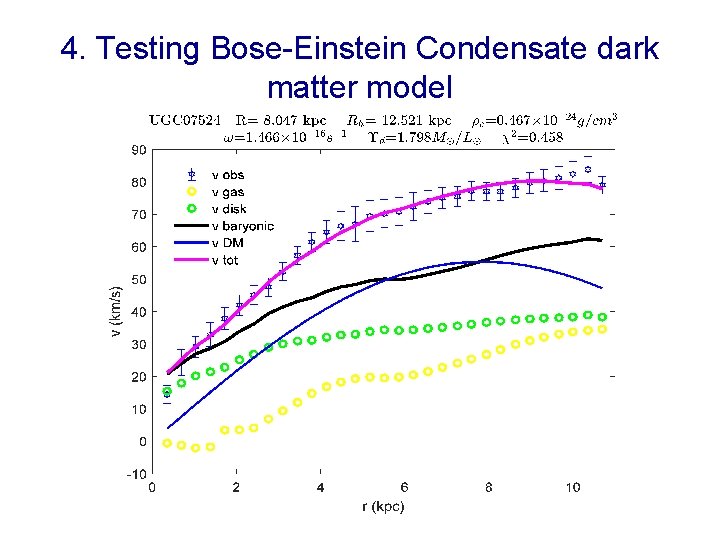
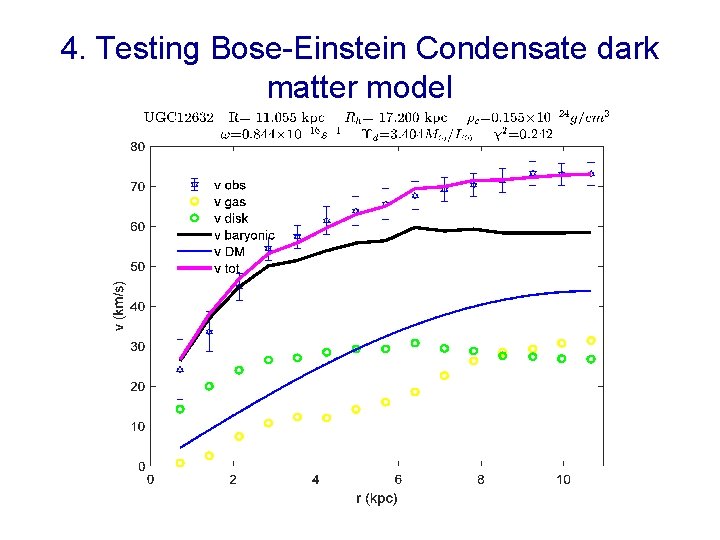
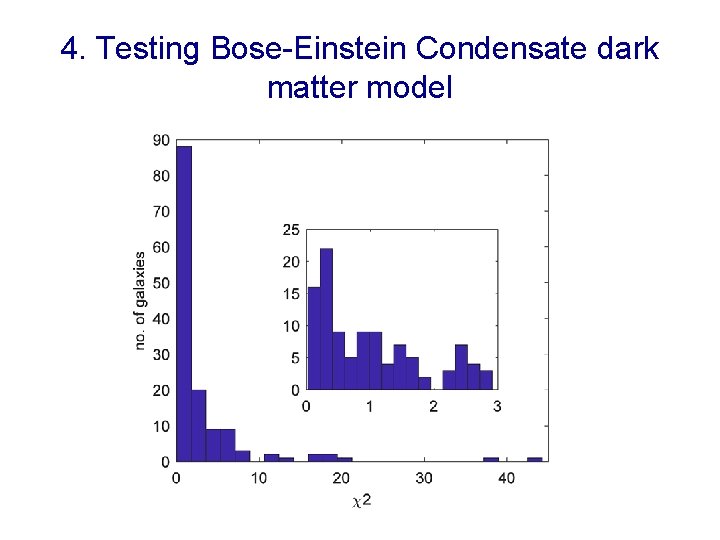
4. Testing the Bose-Einstein Condensate dark matter model •
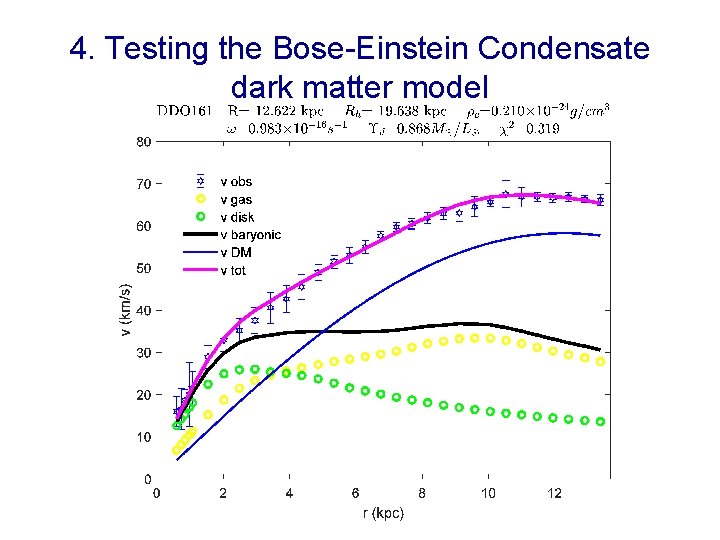
4. Testing the Bose-Einstein Condensate dark matter model
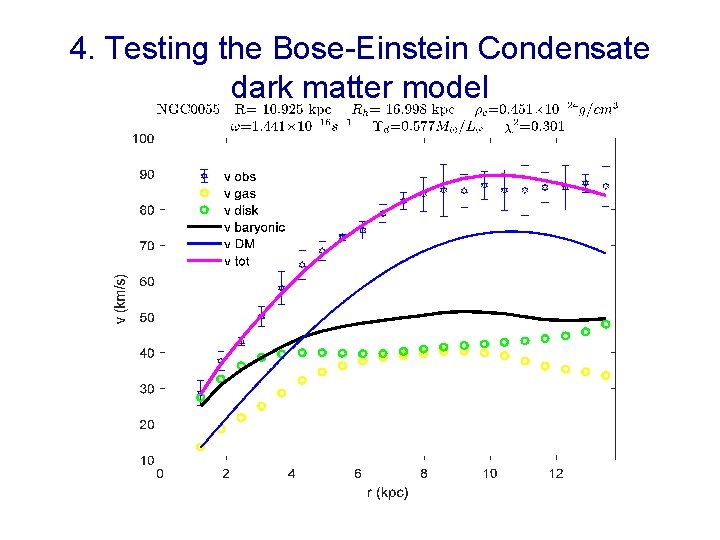
4. Testing the Bose-Einstein Condensate dark matter model
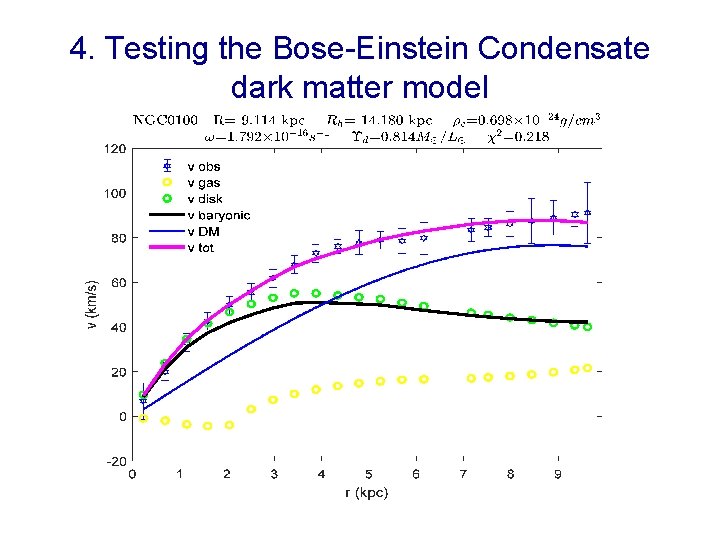
4. Testing the Bose-Einstein Condensate dark matter model
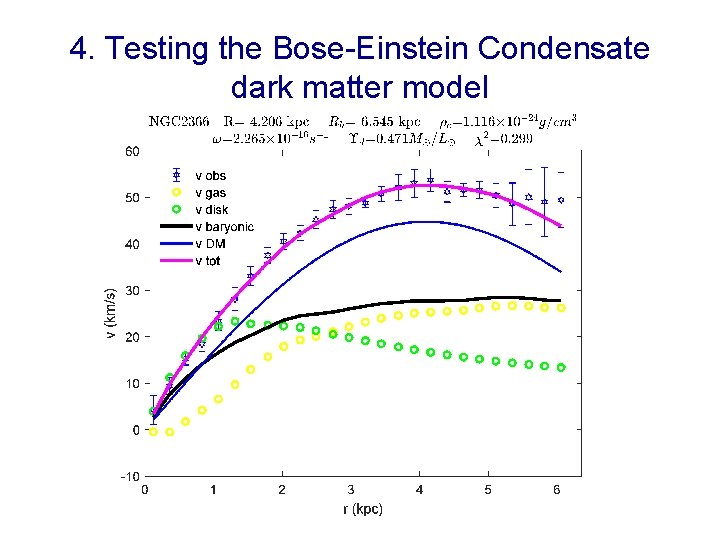
4. Testing the Bose-Einstein Condensate dark matter model
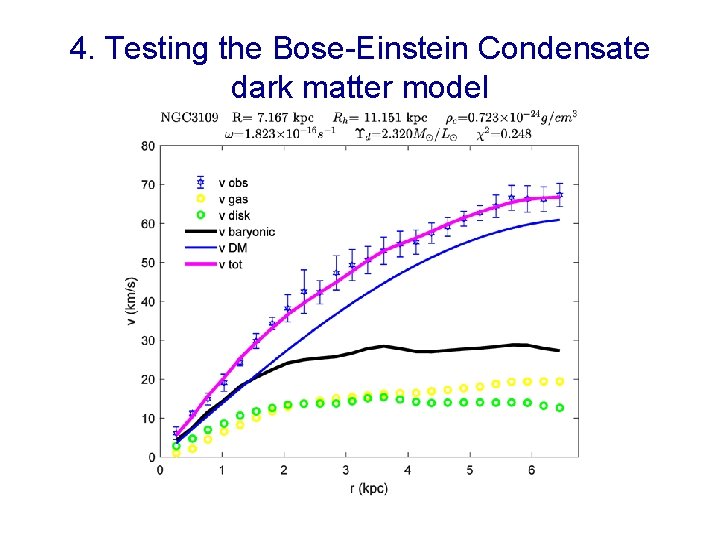
4. Testing the Bose-Einstein Condensate dark matter model
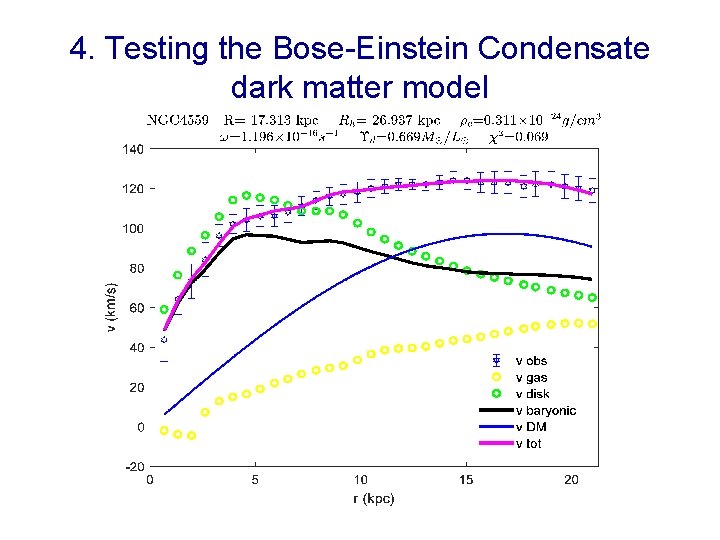
4. Testing the Bose-Einstein Condensate dark matter model
4. Testing the Bose-Einstein Condensate dark matter model
4. Testing Bose-Einstein Condensate dark matter model
4. Testing Bose-Einstein Condensate dark matter model
4. Testing Bose-Einstein Condensate dark matter model

4. Testing the Bose-Einstein Condensate dark matter model • The mass of the particle in the condensate can be obtained as From cosmological considerations (Boyanovski et al. , PRD 77, 043518 2008) is the number of internal degrees of freedom

4. Testing the Bose-Einstein Condensate dark matter model

4. Testing the Bose-Einstein Condensate dark matter model •

7. Conclusions • -galactic rotation curves pose a major challenge to present day physics • -they can be explained in models in which dark matter is in the form of a Bose. Einstein condensate • -this model provides a good description of the galactic rotation curves • -all relevant predicted quantities can be compared directly with observations

7. Conclusions • -a powerful observational tool for discriminating between standard dark matter and Bose-Einstein condensed model is the study of the deflection of light • -the gravitational deflection angle predicted by the Bose-Einstein models is much larger as compared to the values predicted by the standard isothermal dark halo models • -the study of the gravitational lensing may provide direct evidence for the existence of the Bose-Einstein condensation at cosmic scale
- Slides: 42