Testing the approach Experimental Condition Control Condition Please

Testing the approach Experimental Condition Control Condition Please wait 3 seconds.

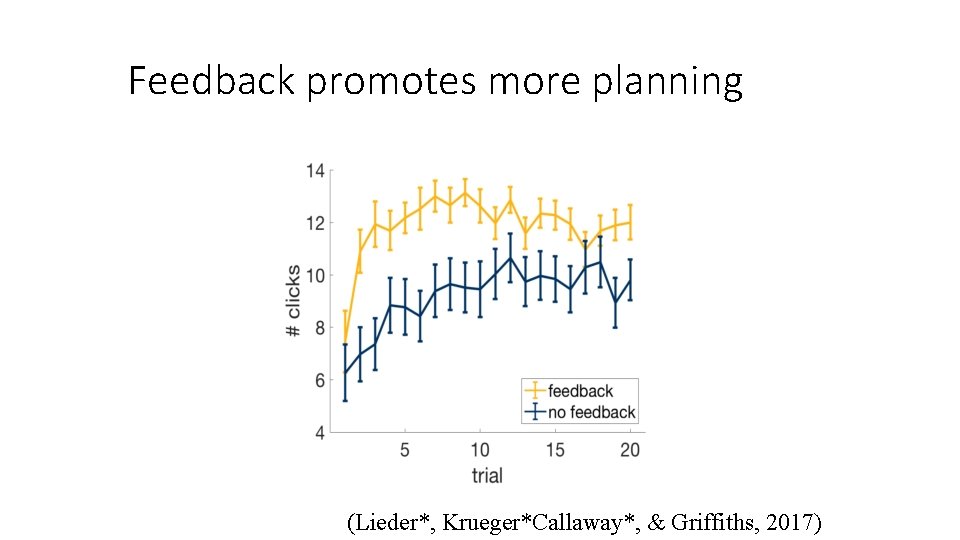
Feedback promotes more planning (Lieder*, Krueger*Callaway*, & Griffiths, 2017)

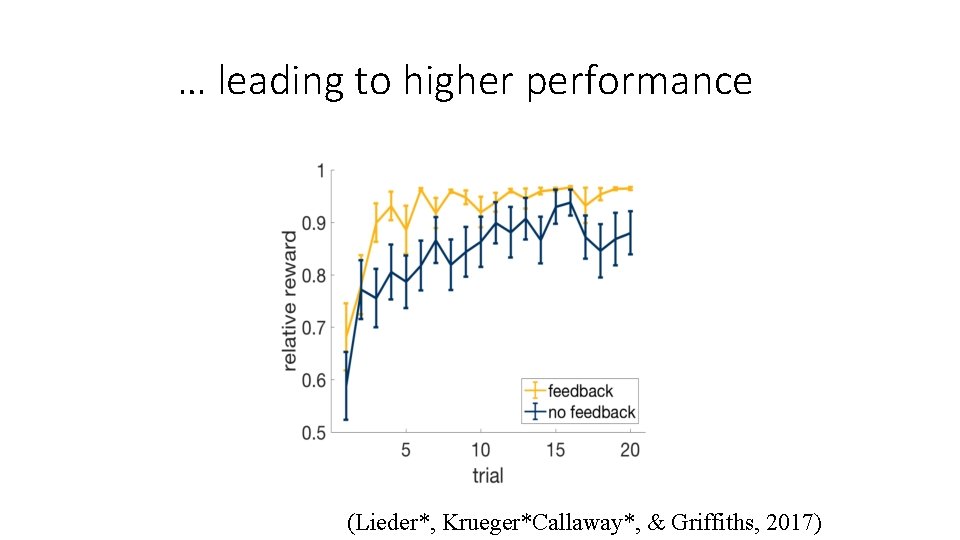
… leading to higher performance (Lieder*, Krueger*Callaway*, & Griffiths, 2017)

Conclusions • Resource rationality provides a framework that is realistic yet still systematic as a source of models • Many standard heuristics are not just “kluges” but are resource-rational for some architecture • This approach lets us tackle questions about how people use their cognitive resources, and how to design systems to overcome those limitations

Availability of extreme events • Availability bias: people over-estimate the probability of events that come to mind easily (Tversky & Kahneman, 1973) • Extreme events come to mind easily…

Availability of extreme events • Task: Estimate the expected utility of an action • Architecture: Generate (weighted) samples of possible outcomes of the action • Cost: Increases linearly in the number of samples (as with opportunity cost) (Lieder, Hsu, & Griffiths, 2014)

Unbiased sampling is bad…

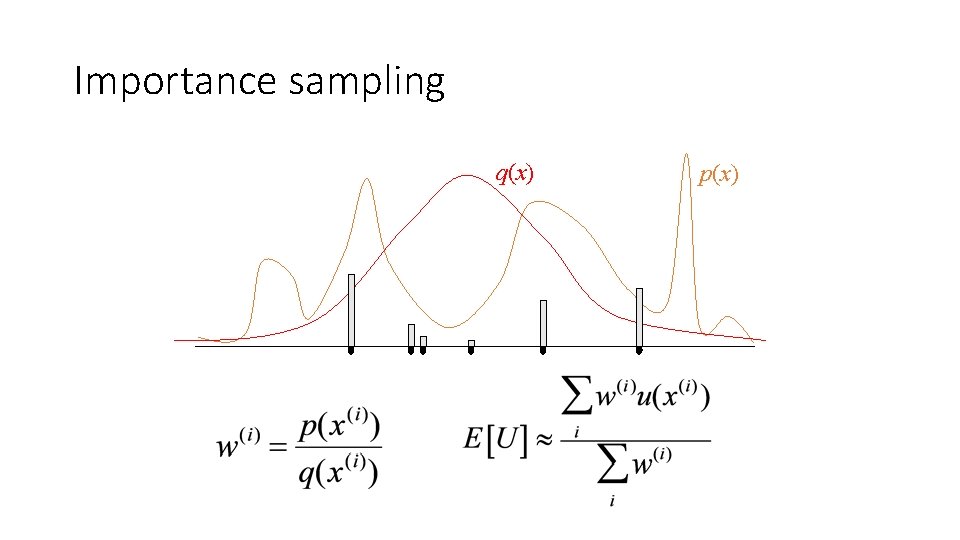
Importance sampling q(x) p(x)

The optimal distribution • Variance is minimized by… • But, the result is biased: with small samples, we will over-represent extreme events (Lieder, Hsu, & Griffiths, 2014)

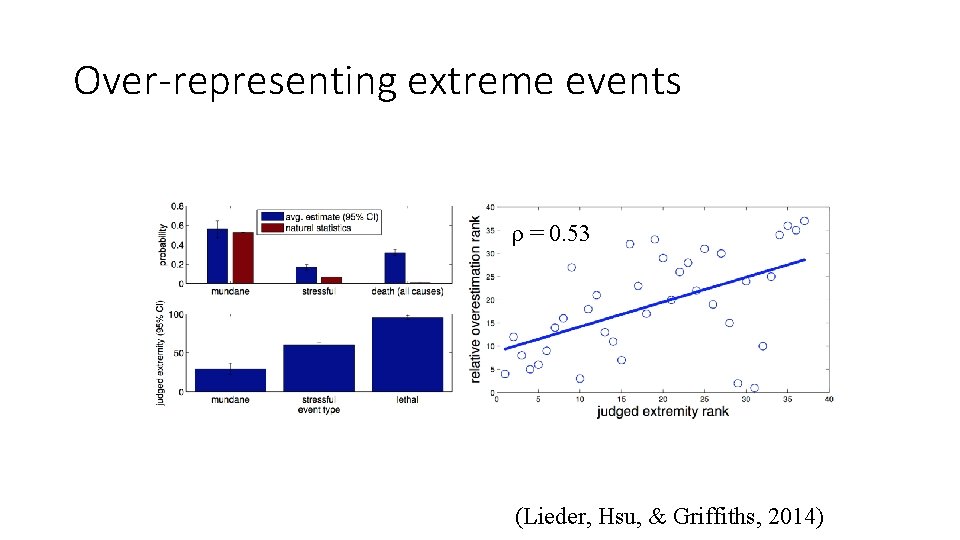
Over-representing extreme events ρ = 0. 53 (Lieder, Hsu, & Griffiths, 2014)

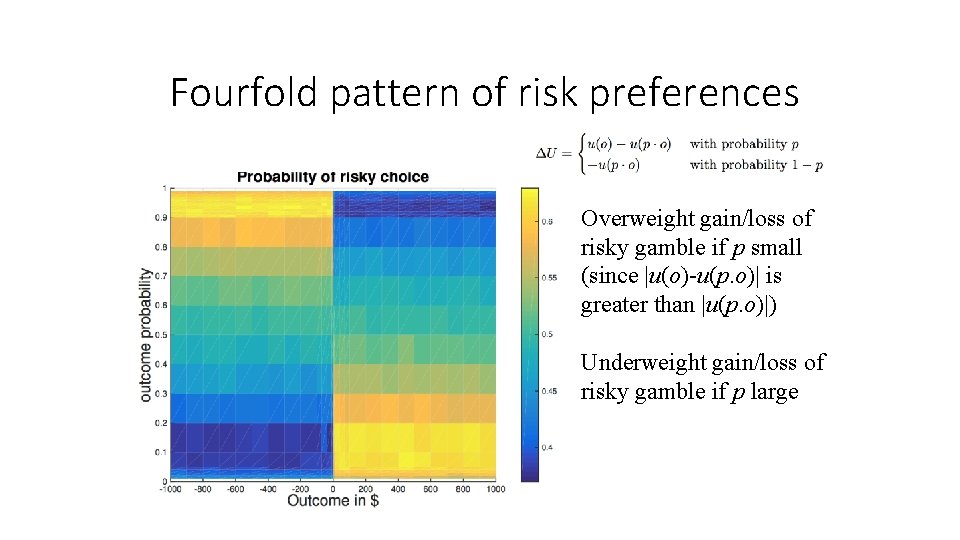
A simple optimal heuristic • When making a decision… • generate from the utility-weighted distribution • tally the number of pros and cons • Reproduces phenomena in decision-making • fourfold pattern of risk preferences (Tversky & Kahneman, 1992) • Allais paradox (Allais, 1953) • outperforms cumulative prospect theory in the Technion dataset (Erev et al. , 2010)

Fourfold pattern of risk preferences Overweight gain/loss of risky gamble if p small (since |u(o)-u(p. o)| is greater than |u(p. o)|) Underweight gain/loss of risky gamble if p large

Allais paradox L 1: 66% chance of $2400, 33% chance of $2500, 1% chance of $0 L 2: 100% chance of $2400 L 1: 33% chance of $2500, 67% chance of $0 L 2: 34% chance of $2400, 66% chance of $0

Allais paradox

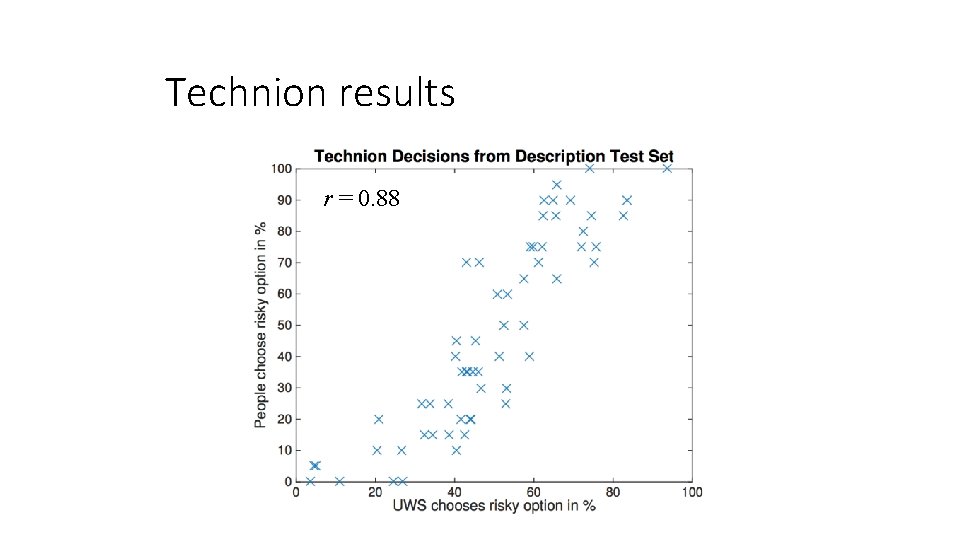
Technion results r = 0. 88

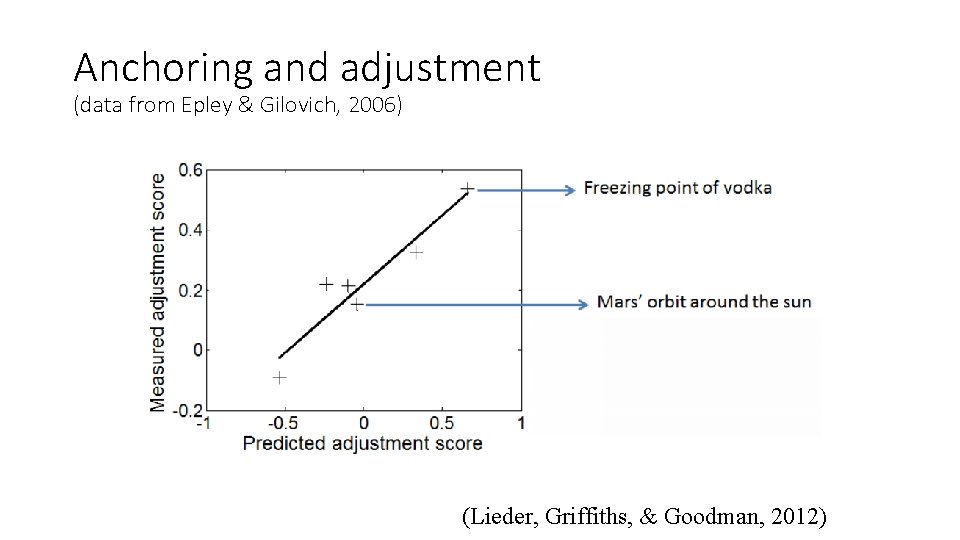
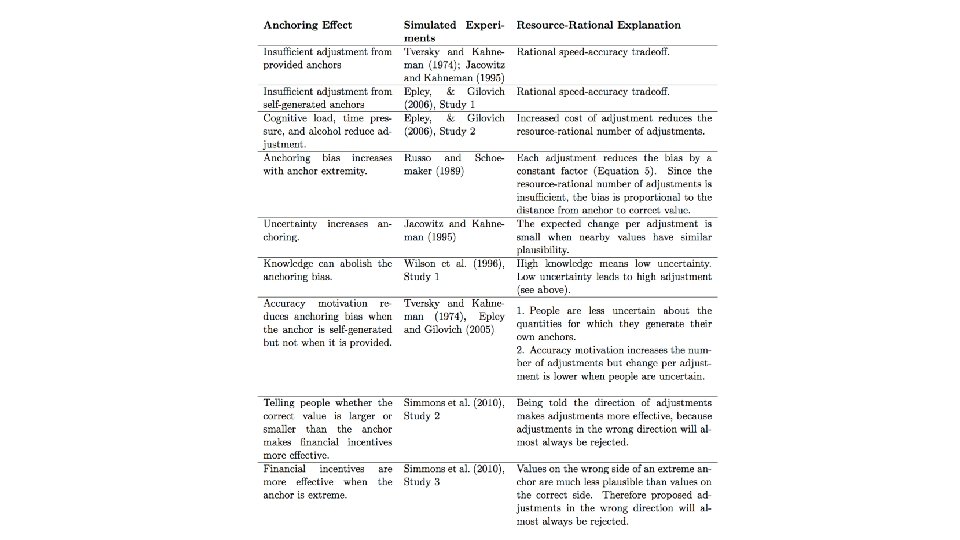
Anchoring and adjustment • What’s the freezing point of vodka? • How long is Mars’ orbit around the sun? • People answer these questions by starting with a more familiar example (an anchor) and adjusting away from it (leading to bias) (Epley & Gilovich, 2006)

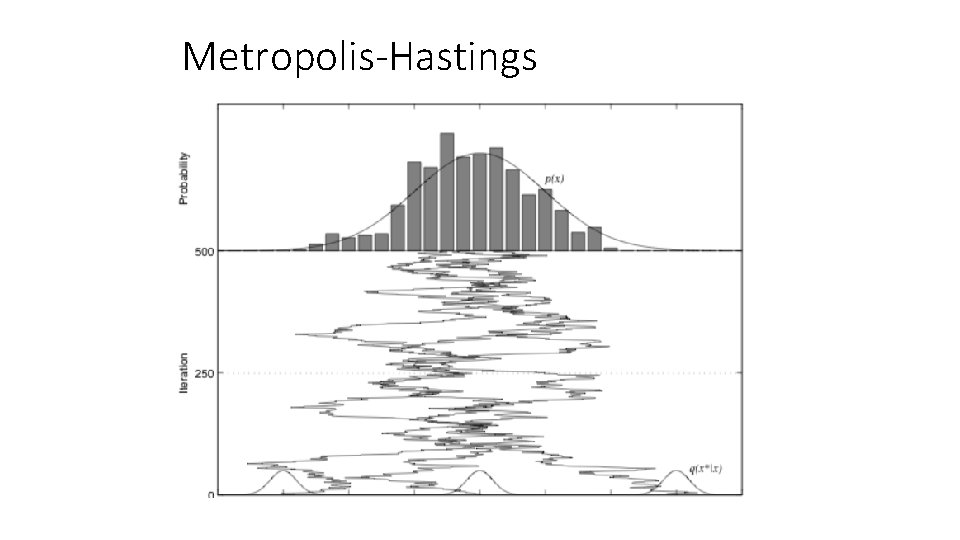
Anchoring and adjustment • Task: Estimate a quantity based on memory and other cues • Architecture: Markov chain Monte Carlo via the Metropolis-Hastings algorithm • Cost: Increases linearly in the number of samples (as with opportunity cost) (Lieder, Griffiths, & Goodman, 2012)

Metropolis-Hastings

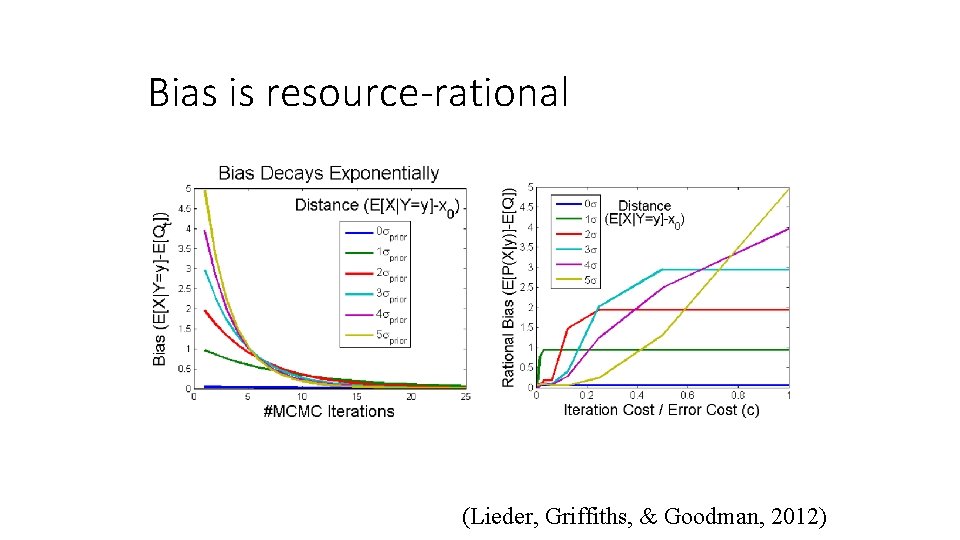
Bias is resource-rational (Lieder, Griffiths, & Goodman, 2012)

Anchoring and adjustment (data from Epley & Gilovich, 2006) (Lieder, Griffiths, & Goodman, 2012)

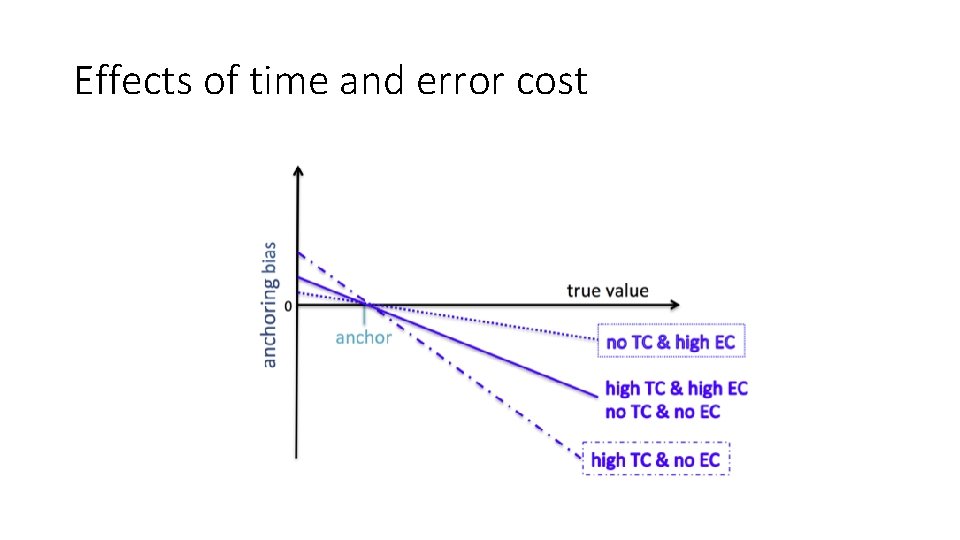
Other predictions • Cognitive load, time pressure, and alcohol reduce adjustment (Epley & Gilovich, 2006) • Bias increases with anchor extremity (Russo & Schoemaker, 1989) • Uncertainty increases anchoring (Jacowitz & Kahneman, 1995) • Knowledge can abolish the anchoring bias (Wilson et al. , 1996)

Effects of time and error cost

Waiting for the bus

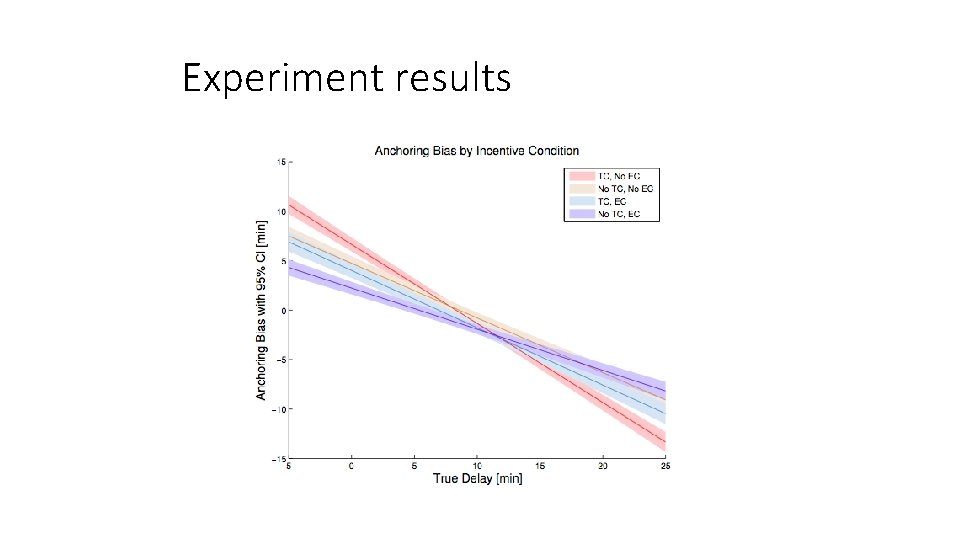
Experiment results

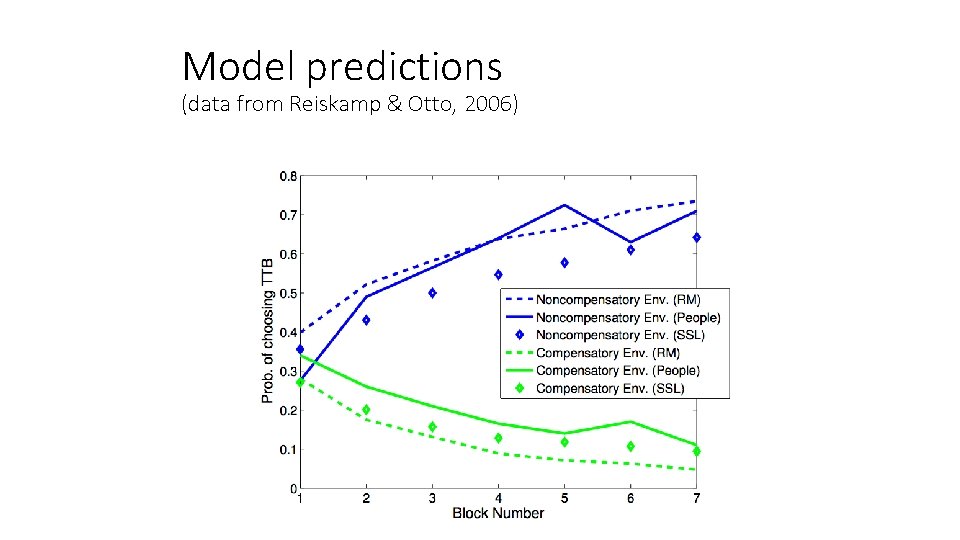
Investment task Two strategies: Take The Best (TTB) vs. weighted combination Two environments: noncompensatory vs. compensatory (Lieder & Griffiths, submitted)

Model predictions (data from Reiskamp & Otto, 2006)

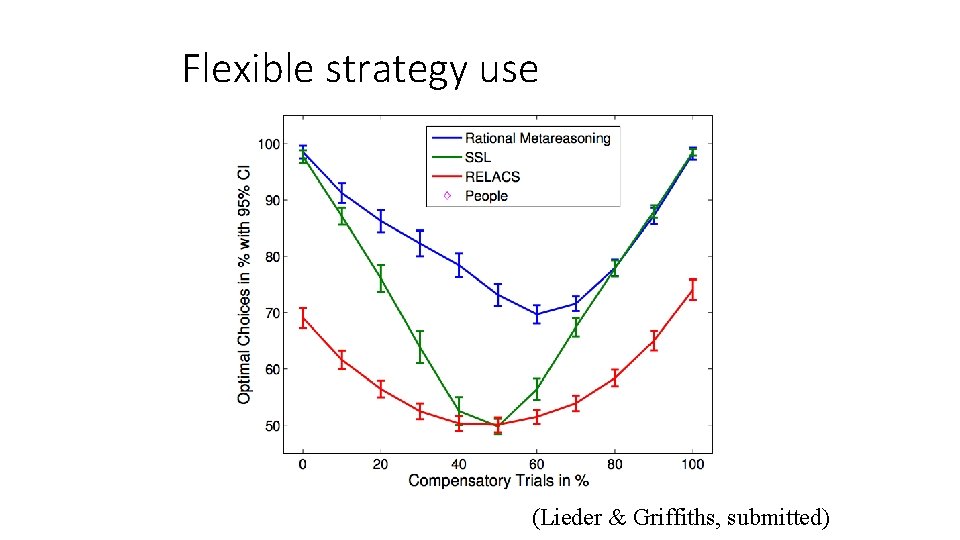
Flexible strategy use (Lieder & Griffiths, submitted)