Testing Statistical Hypothesis for Dependent Samples 1 Testing

Testing Statistical Hypothesis for Dependent Samples 1

Testing Hypotheses about Two Dependent Means n n n 2 Dependent Groups t-test Paired Samples t-test Correlated Groups t-test

Steps in Test of Hypothesis 1. 2. 3. 4. 5. 6. 3 Determine the appropriate test Establish the level of significance: α Determine whether to use a one tail or two tail test Same as Before Calculate the test statistic Determine the degree of freedom Compare computed test statistic against a tabled/critical value

1. Determine the appropriate test 1. 2. When means are computed for the same group of people at two different points in time (e. g. , before and after intervention) When subjects in one group are paired to subjects in the second group on the basis of some attribute. Examples: n n n 4 Husbands versus wives First-born children versus younger siblings AIDS patients versus their primary caretakers

1. Determine the appropriate test 3. Researchers sometimes deliberately pairmatch subjects in one group with unrelated subjects in another group to enhance the comparability of the two groups. n 5 For example, people with lung cancer might be pairmatched to people without lung cancer on the basis of age, education, and gender, and then the smoking behavior of the two groups might be compared.

Example: Two Interventions in Same Patients n Suppose that we wanted to compare direct and indirect methods of blood pressure measurement in a sample of trauma patients. Blood pressure values (mm Hg) are obtained from 10 patients via both methods: n n 6 X 1 = Direct method: radial arterial catheter X 2 = Indirect method: the bell component of the stethoscope

2. Establish Level of Significance n n α is a predetermined value The convention α =. 05 n α =. 01 n α =. 001 n 7

3. Determine Whether to Use a One or Two Tailed Test n n H 0 : µ D = 0 Ha : µ D 0 Mean of differences across patients 8 Two Tailed Test if no direction is specified

3. Determine Whether to Use a One or Two Tailed Test n n H 0 : µ D = 0 Ha : µ D 0 One Tailed Test if direction is specified 9

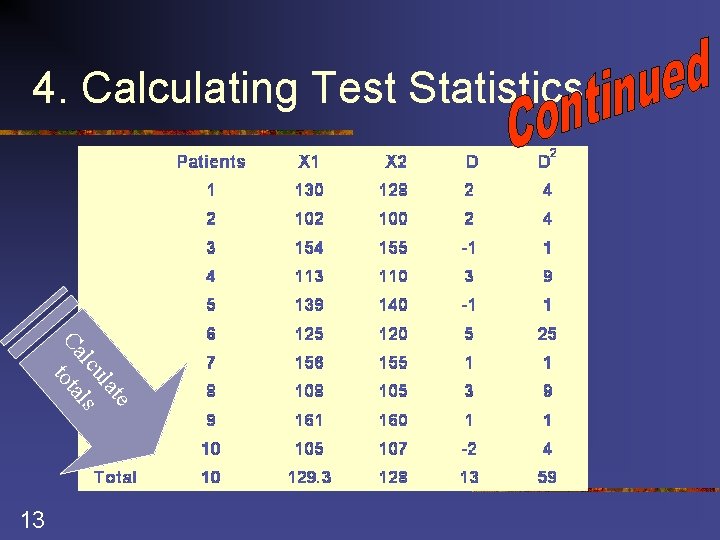
4. Calculating Test Statistics Av dif era fer ge en of ce s d of r a n d an tio ces t S via en e fer D if d Sta nda Err rd o diff r of ere nce s Sa 10 mp le siz e How to calculate standard deviation of differences

4. Calculating Test Statistics Defining Formula 11 Calculating Formula

12 Squared differences Diff eren obse ce o f rvat ions Obs erva tion 1 an sam d 2 on s e pa tien t 4. Calculating Test Statistics

4. Calculating Test Statistics e lat lcu ls Ca tota 13

4. Calculating Test Statistics 14

4. Calculating Test Statistics n 15 Calculate t-statistic from average of differences and standard error of differences

5. Determine Degrees of Freedom n n n 16 Degrees of freedom, df, is value indicating the number of independent pieces of information a sample can provide for purposes of statistical inference. Df = Sample size – Number of parameters estimated Df for paired t-test is n minus 1

6. Compare the Computed Test Statistic Against a Tabled Value n n α =. 05 Df = n-1 = 9 n tα(df n n 17 = 9) = 2. 26 Two tailed tα(df = 9) = 1. 83 One tailed Reject H 0 if tc is greater than tα

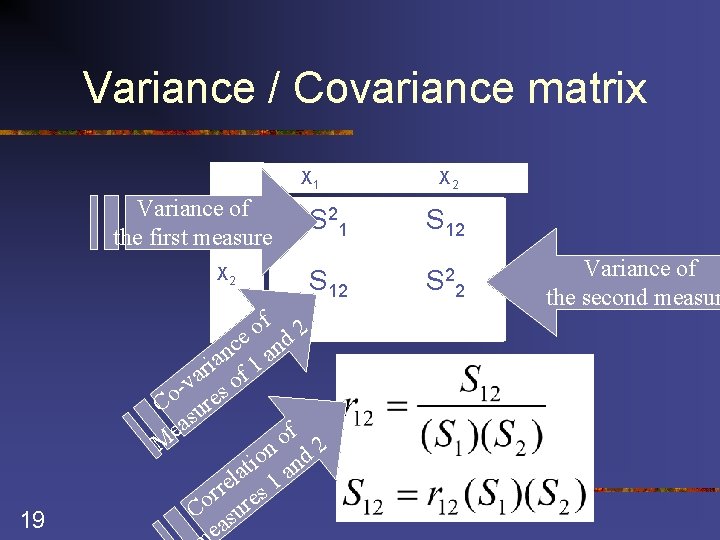
Alternative Approach Estimating Standard deviation of differences from sample standard deviations 18

Variance / Covariance matrix X 1 Variance. X 1 of the first measure X 2 19 X 2 S 21 S 12 S 22 f 2 o e nd c n a a i r f 1 a -v es o o C sur ea f o M 2 n o d i an t a l 1 e r r res o C su ea Variance of the second measur

Variance / Covariance matrix X 1 X 2 S 21 S 22 Standard error of difference can be calculated from above table 20

21 Coiance Var rre bett melaasu tio re oftw. Firs w o m een n eas ure s Standard deviation of First measure Standard deviation of second measure Variance of second measure of or e rr s a rd c e nd ren S t a D i ffe Alternative Approach for Calculating standard Error

Correlation Matrix Direct Pearson Correlation Sum of Squares and Cross-products Covariance N Indirect Pearson Correlation Sum of Squares and Cross-products Covariance N 22 Direct 1 Indirect. 996(**) 4496. 100 499. 567 10 4611. 00 512. 333 10 . 996(**) 1 4611. 00 512. 333 10 4768. 00 529. 778 10

Alternative Approach for Calculating standard Error Same value as before 23

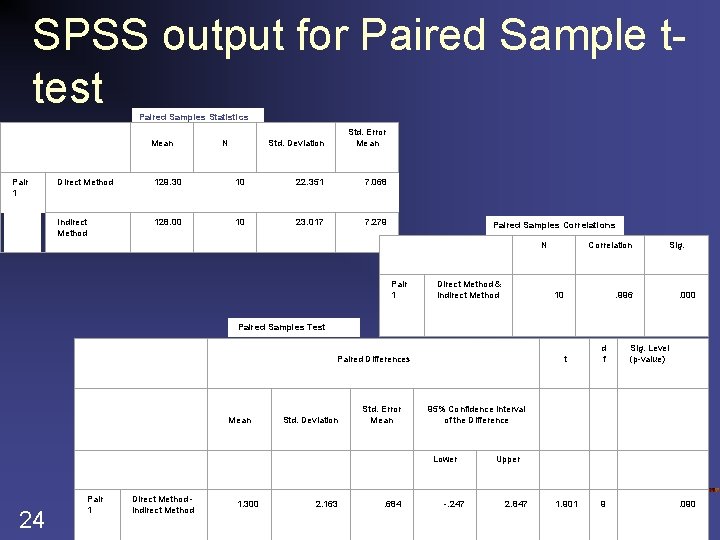
SPSS output for Paired Sample ttest Paired Samples Statistics Mean Pair 1 N Std. Deviation Std. Error Mean Direct Method 129. 30 10 22. 351 7. 068 Indirect Method 128. 00 10 23. 017 7. 279 Paired Samples Correlations N Pair 1 Direct Method & Indirect Method Correlation 10 Sig. . 996 . 000 Paired Samples Test Paired Differences Mean Std. Deviation Std. Error Mean 24 Direct Method Indirect Method 1. 300 2. 163 . 684 d f 1. 901 9 Sig. Level (p-value) 95% Confidence Interval of the Difference Lower Pair 1 t -. 247 Upper 2. 847 . 090

Take Home Lesson How to compare means of paired dependent samples 25