Testing of Logic Circuits z Fault Models z

Testing of Logic Circuits z Fault Models z Test Generation and Coverage z Fault Detection z Design for Test CS 150 - Spring 2008 – Lec. #17: Testing - 1

Fault Model z Stuck-At Model y Assume selected wires (gate input or output) are “stuck at” logic value 0 or 1 y Models certain kinds of fabrication flaws that short circuit wires to ground or power, or broken wires that are floating x. Wire w stuck-at-0: w/0 x. Wire w stuck-at-1: w/1 y Often assume there is only one fault at a time—even though in real circuits multiple simultaneous faults are possible and can mask each other y Obviously a very simplistic model! CS 150 - Spring 2008 – Lec. #17: Testing - 2

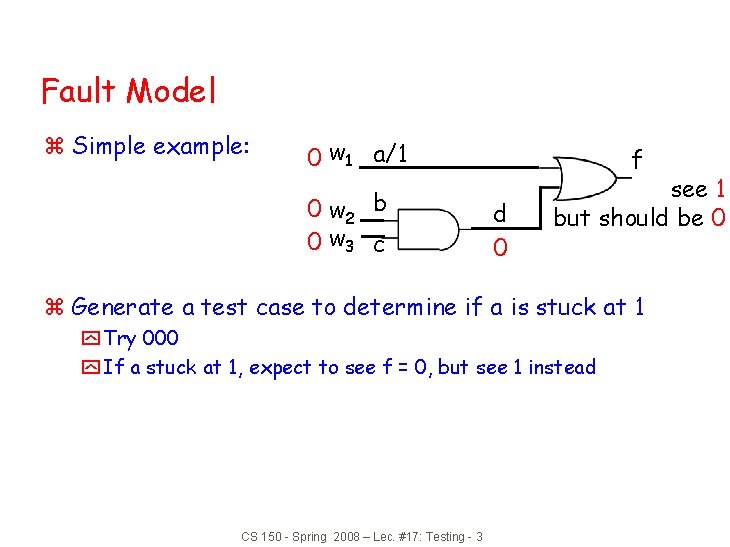
Fault Model z Simple example: 0 w 1 a/1 b 0 w 2 0 w 3 c f d 0 see 1 but should be 0 z Generate a test case to determine if a is stuck at 1 y Try 000 y If a stuck at 1, expect to see f = 0, but see 1 instead CS 150 - Spring 2008 – Lec. #17: Testing - 3

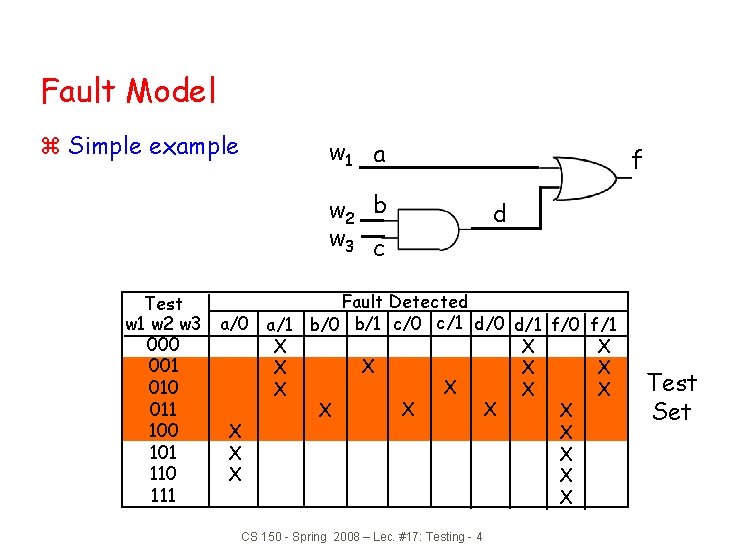
Fault Model z Simple example w 1 a w 2 b w 3 c f d Fault Detected Test w 1 w 2 w 3 a/0 a/1 b/0 b/1 c/0 c/1 d/0 d/1 000 X X 001 X X 010 X X 011 X X X 100 X 101 X 110 X 111 CS 150 - Spring 2008 – Lec. #17: Testing - 4 f/0 f/1 X X X X Test Set

Problems with Fault Model z In general, n-input circuits require much less than 2 n test inputs to cover all possible stuck-at-faults in the circuit z However, this number is usually still too large in real circuits for practical purposes z Finding minimum test cover is an NP-hard problem too y Finding even if a lead is untestable is also NP-hard (reducible to SAT) CS 150 - Spring 2008 – Lec. #17: Testing - 5

Path Sensitization z Wire-at-time testing too laborious z Better to focus on wiring paths, enabling multi-wire testing at the same time z “Activate” or “Sensitize” a path so that changes in signal propagating along the path affects the output y Very similar to “false paths” in timing analysis y Key difference: we can neglect timing in considering sensitization CS 150 - Spring 2008 – Lec. #17: Testing - 6

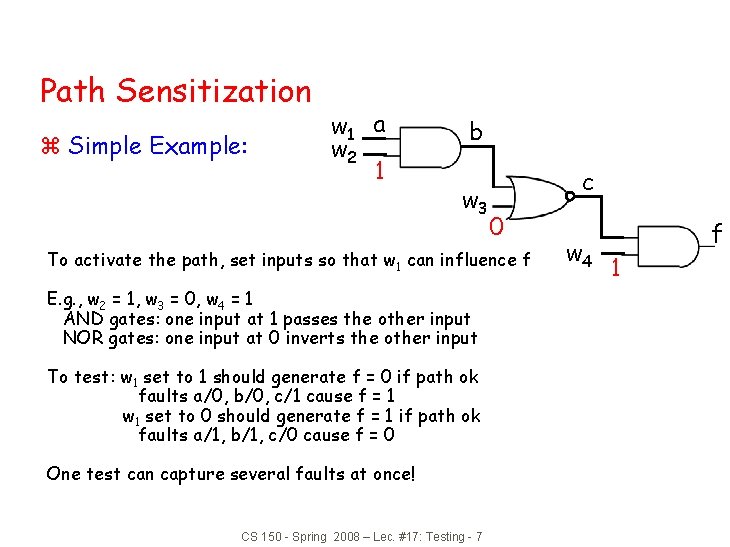
Path Sensitization z Simple Example: w 1 a w 2 1 b w 3 c 0 To activate the path, set inputs so that w 1 can influence f E. g. , w 2 = 1, w 3 = 0, w 4 = 1 AND gates: one input at 1 passes the other input NOR gates: one input at 0 inverts the other input To test: w 1 set to 1 should generate f = 0 if path ok faults a/0, b/0, c/1 cause f = 1 w 1 set to 0 should generate f = 1 if path ok faults a/1, b/1, c/0 cause f = 0 One test can capture several faults at once! CS 150 - Spring 2008 – Lec. #17: Testing - 7 w 4 f 1

Path Sensitization z Good news: one test checks for several faults y Number of paths usually smaller than number of wires y Still an impractically large number of paths for large-scale circuits z Path idea can be used to “propagate” a fault to the output to observe the fault y Set inputs and intermediate values so as to pass an internal wire to the output while setting inputs to drive that internal wire to a known value y If propagated value isn’t as expected, then we have found a fault on the isolated wire z The “D” algorithm y Set fault point at circuit to “D” y Propagate “D” along path to the output CS 150 - Spring 2008 – Lec. #17: Testing - 8

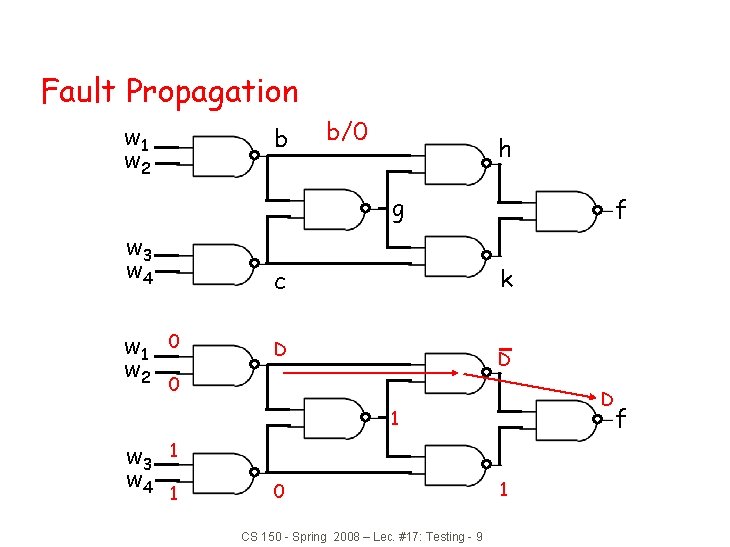
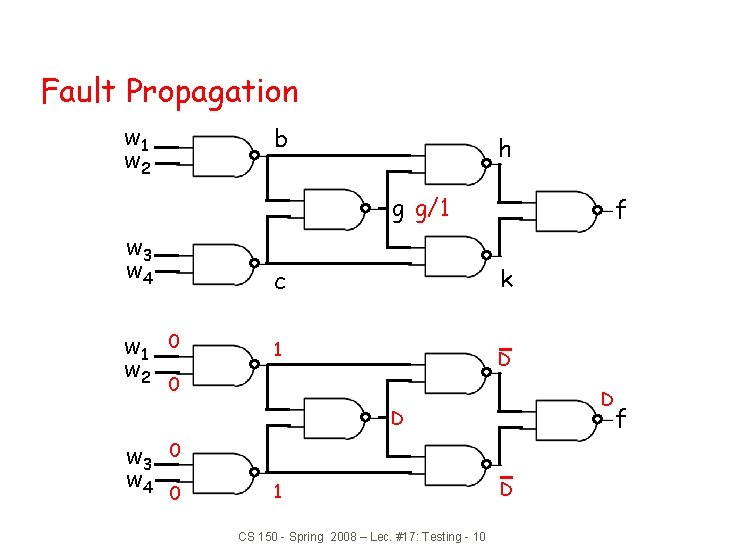
Fault Propagation w 1 w 2 b b/0 h g w 3 w 4 w 1 w 2 k c 0 f D D 0 D 1 w 3 w 4 1 1 0 CS 150 - Spring 2008 – Lec. #17: Testing - 9 1 f

Fault Propagation w 1 w 2 b h g g/1 w 3 w 4 w 1 w 2 k c 0 f 1 D 0 D D w 3 w 4 0 0 1 CS 150 - Spring 2008 – Lec. #17: Testing - 10 D f

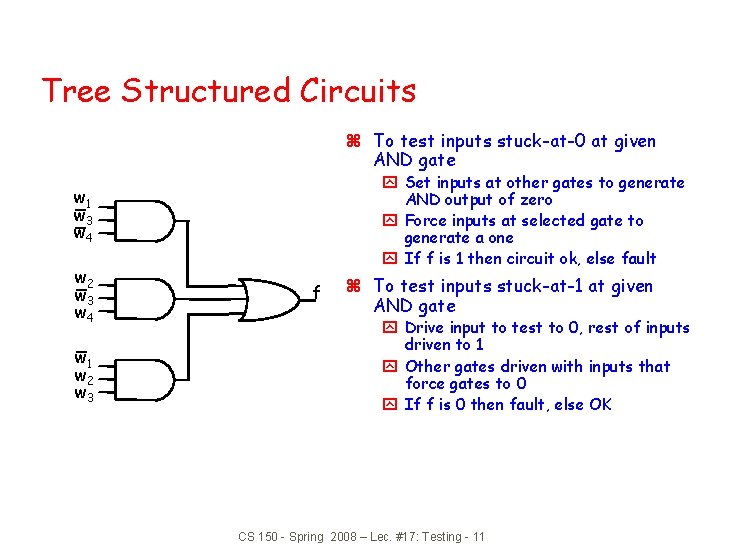
Tree Structured Circuits z To test inputs stuck-at-0 at given AND gate y Set inputs at other gates to generate AND output of zero y Force inputs at selected gate to generate a one y If f is 1 then circuit ok, else fault w 1 w 3 w 4 w 2 w 3 w 4 w 1 w 2 w 3 f z To test inputs stuck-at-1 at given AND gate y Drive input to test to 0, rest of inputs driven to 1 y Other gates driven with inputs that force gates to 0 y If f is 0 then fault, else OK CS 150 - Spring 2008 – Lec. #17: Testing - 11

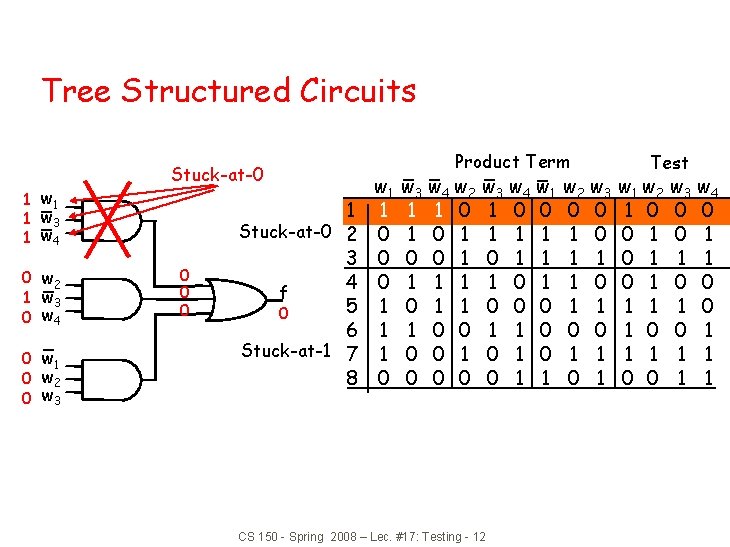
Tree Structured Circuits 1 w 1 1 w 3 1 w 4 0 w 2 1 w 3 0 w 4 0 w 1 0 w 2 0 w 3 Stuck-at-0 0 1 Stuck-at-0 2 3 4 f 5 0 6 Stuck-at-1 7 8 w 1 1 0 0 0 1 1 1 0 Product Term w 3 w 4 w 2 1 1 0 1 0 0 1 1 1 0 0 0 w 3 w 4 w 1 1 0 0 1 1 1 0 1 0 0 0 1 1 CS 150 - Spring 2008 – Lec. #17: Testing - 12 w 3 0 0 1 1 1 0 0 1 1 0 1 Test w 1 w 2 1 0 0 1 0 1 1 0 0 w 3 w 4 0 0 0 1 1 1

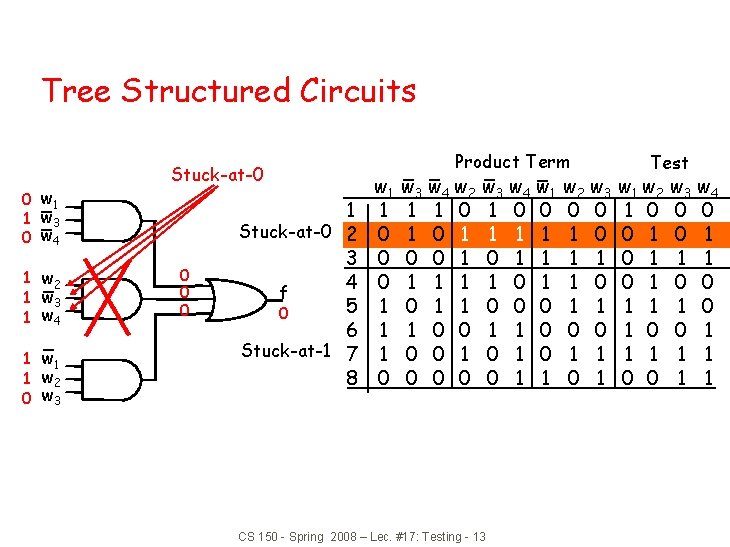
Tree Structured Circuits 0 w 1 1 w 3 0 w 4 1 w 2 1 w 3 1 w 4 1 w 1 1 w 2 0 w 3 Stuck-at-0 0 1 Stuck-at-0 2 3 4 f 5 0 6 Stuck-at-1 7 8 w 1 1 0 0 0 1 1 1 0 Product Term w 3 w 4 w 2 1 1 0 1 0 0 1 1 1 0 0 0 w 3 w 4 w 1 1 0 0 1 1 1 0 1 0 0 0 1 1 CS 150 - Spring 2008 – Lec. #17: Testing - 13 w 2 w 3 0 0 1 1 1 0 0 1 1 0 1 Test w 1 w 2 1 0 0 1 0 1 1 0 0 w 3 w 4 0 0 0 1 1 1

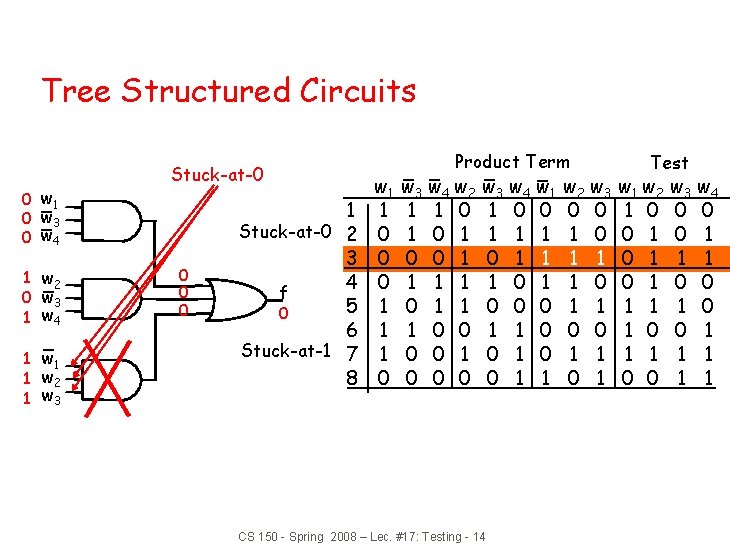
Tree Structured Circuits 0 w 1 0 w 3 0 w 4 1 w 2 0 w 3 1 w 4 1 w 1 1 w 2 1 w 3 Stuck-at-0 0 1 Stuck-at-0 2 3 4 f 5 0 6 Stuck-at-1 7 8 w 1 1 0 0 0 1 1 1 0 Product Term w 3 w 4 w 2 1 1 0 1 0 0 1 1 1 0 0 0 w 3 w 4 w 1 1 0 0 1 1 1 0 1 0 0 0 1 1 CS 150 - Spring 2008 – Lec. #17: Testing - 14 w 2 w 3 0 0 1 1 1 0 0 1 1 0 1 Test w 1 w 2 1 0 0 1 0 1 1 0 0 w 3 w 4 0 0 0 1 1 1

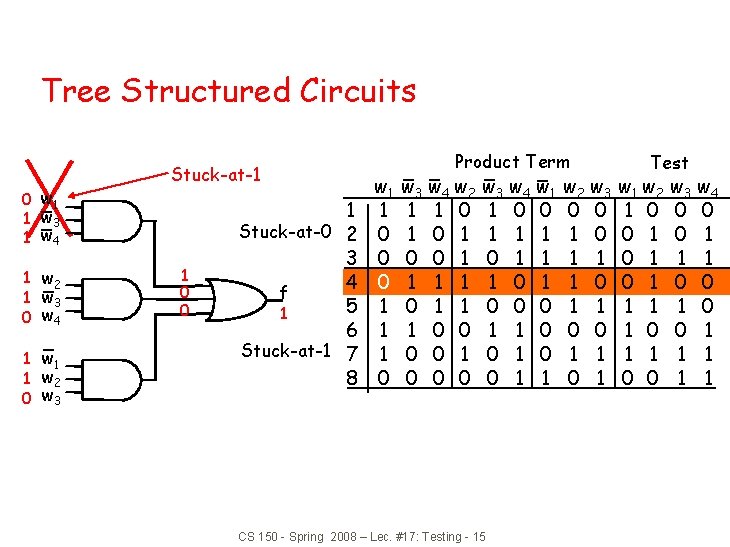
Tree Structured Circuits 0 w 1 1 w 3 1 w 4 1 w 2 1 w 3 0 w 4 1 w 1 1 w 2 0 w 3 Stuck-at-1 1 0 0 1 Stuck-at-0 2 3 4 f 5 1 6 Stuck-at-1 7 8 w 1 1 0 0 0 1 1 1 0 Product Term w 3 w 4 w 2 1 1 0 1 0 0 1 1 1 0 0 0 w 3 w 4 w 1 1 0 0 1 1 1 0 1 0 0 0 1 1 CS 150 - Spring 2008 – Lec. #17: Testing - 15 w 2 w 3 0 0 1 1 1 0 0 1 1 0 1 Test w 1 w 2 1 0 0 1 0 1 1 0 0 w 3 w 4 0 0 0 1 1 1

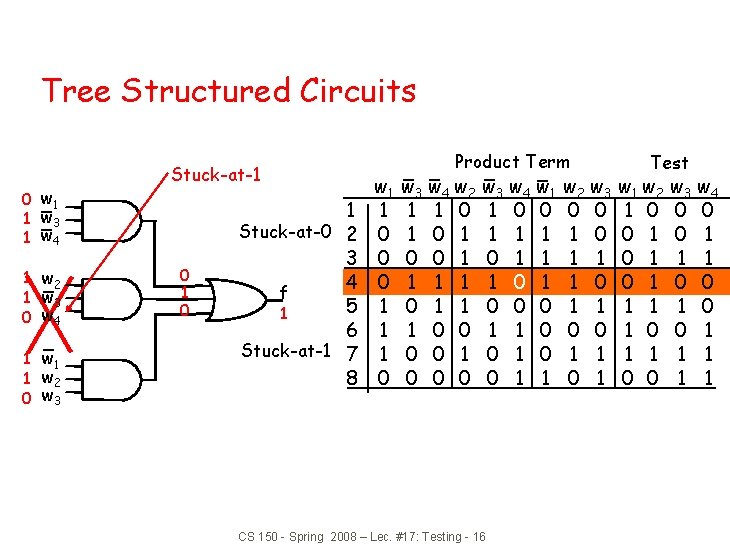
Tree Structured Circuits 0 w 1 1 w 3 1 w 4 1 w 2 1 w 3 0 w 4 1 w 1 1 w 2 0 w 3 Stuck-at-1 0 1 Stuck-at-0 2 3 4 f 5 1 6 Stuck-at-1 7 8 w 1 1 0 0 0 1 1 1 0 Product Term w 3 w 4 w 2 1 1 0 1 0 0 1 1 1 0 0 0 w 3 w 4 w 1 1 0 0 1 1 1 0 1 0 0 0 1 1 CS 150 - Spring 2008 – Lec. #17: Testing - 16 w 2 w 3 0 0 1 1 1 0 0 1 1 0 1 Test w 1 w 2 1 0 0 1 0 1 1 0 0 w 3 w 4 0 0 0 1 1 1

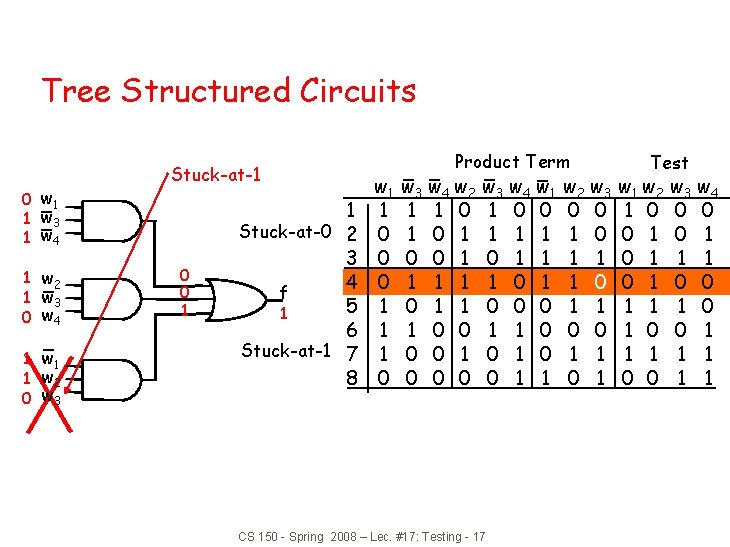
Tree Structured Circuits 0 w 1 1 w 3 1 w 4 1 w 2 1 w 3 0 w 4 1 w 1 1 w 2 0 w 3 Stuck-at-1 0 0 1 1 Stuck-at-0 2 3 4 f 5 1 6 Stuck-at-1 7 8 w 1 1 0 0 0 1 1 1 0 Product Term w 3 w 4 w 2 1 1 0 1 0 0 1 1 1 0 0 0 w 3 w 4 w 1 1 0 0 1 1 1 0 1 0 0 0 1 1 CS 150 - Spring 2008 – Lec. #17: Testing - 17 w 2 w 3 0 0 1 1 1 0 0 1 1 0 1 Test w 1 w 2 1 0 0 1 0 1 1 0 0 w 3 w 4 0 0 0 1 1 1

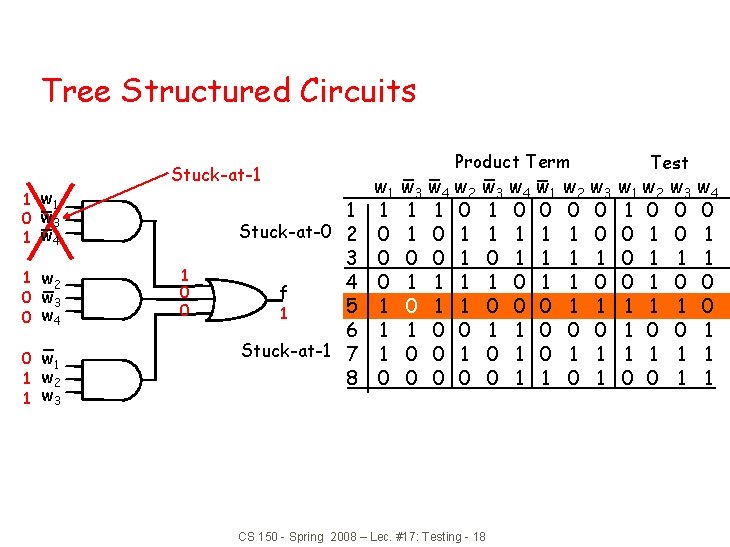
Tree Structured Circuits 1 w 1 0 w 3 1 w 4 1 w 2 0 w 3 0 w 4 0 w 1 1 w 2 1 w 3 Stuck-at-1 1 0 0 1 Stuck-at-0 2 3 4 f 5 1 6 Stuck-at-1 7 8 w 1 1 0 0 0 1 1 1 0 Product Term w 3 w 4 w 2 1 1 0 1 0 0 1 1 1 0 0 0 w 3 w 4 w 1 1 0 0 1 1 1 0 1 0 0 0 1 1 CS 150 - Spring 2008 – Lec. #17: Testing - 18 w 2 w 3 0 0 1 1 1 0 0 1 1 0 1 Test w 1 w 2 1 0 0 1 0 1 1 0 0 w 3 w 4 0 0 0 1 1 1

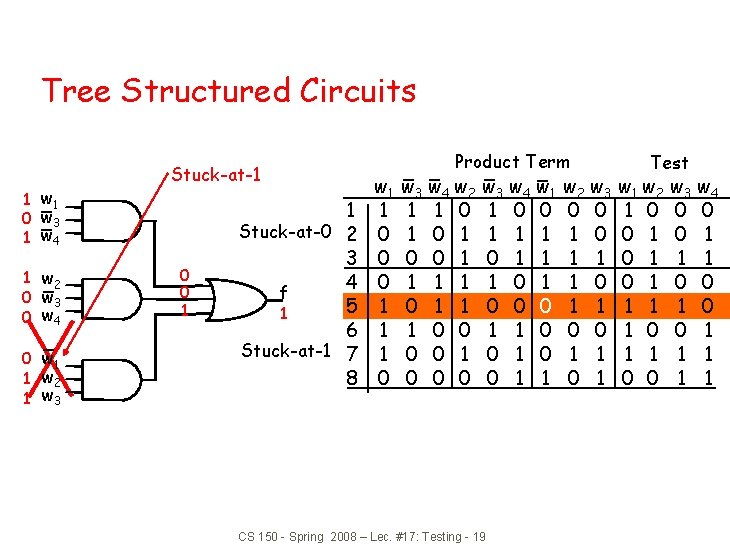
Tree Structured Circuits 1 w 1 0 w 3 1 w 4 1 w 2 0 w 3 0 w 4 0 w 1 1 w 2 1 w 3 Stuck-at-1 0 0 1 1 Stuck-at-0 2 3 4 f 5 1 6 Stuck-at-1 7 8 w 1 1 0 0 0 1 1 1 0 Product Term w 3 w 4 w 2 1 1 0 1 0 0 1 1 1 0 0 0 w 3 w 4 w 1 1 0 0 1 1 1 0 1 0 0 0 1 1 CS 150 - Spring 2008 – Lec. #17: Testing - 19 w 2 w 3 0 0 1 1 1 0 0 1 1 0 1 Test w 1 w 2 1 0 0 1 0 1 1 0 0 w 3 w 4 0 0 0 1 1 1

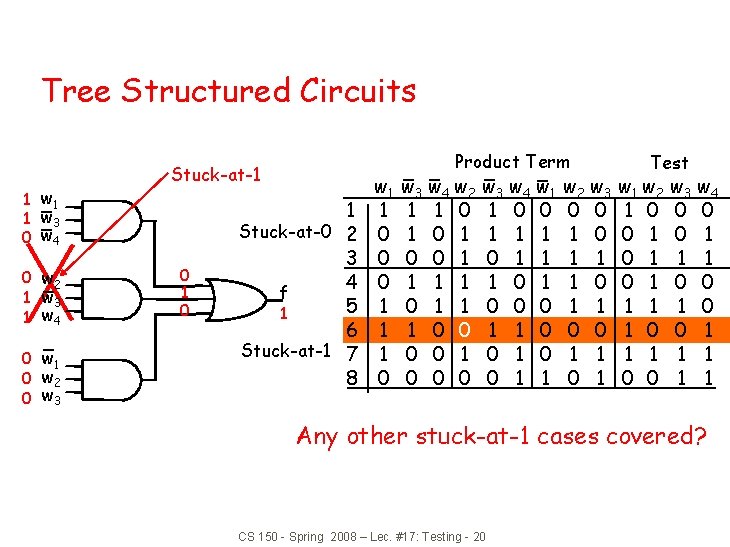
Tree Structured Circuits 1 w 1 1 w 3 0 w 4 0 w 2 1 w 3 1 w 4 0 w 1 0 w 2 0 w 3 Stuck-at-1 0 1 Stuck-at-0 2 3 4 f 5 1 6 Stuck-at-1 7 8 w 1 1 0 0 0 1 1 1 0 Product Term w 3 w 4 w 2 1 1 0 1 0 0 1 1 1 0 0 0 w 3 w 4 w 1 1 0 0 1 1 1 0 1 0 0 0 1 1 w 2 w 3 0 0 1 1 1 0 0 1 1 0 1 Test w 1 w 2 1 0 0 1 0 1 1 0 0 w 3 w 4 0 0 0 1 1 1 Any other stuck-at-1 cases covered? CS 150 - Spring 2008 – Lec. #17: Testing - 20

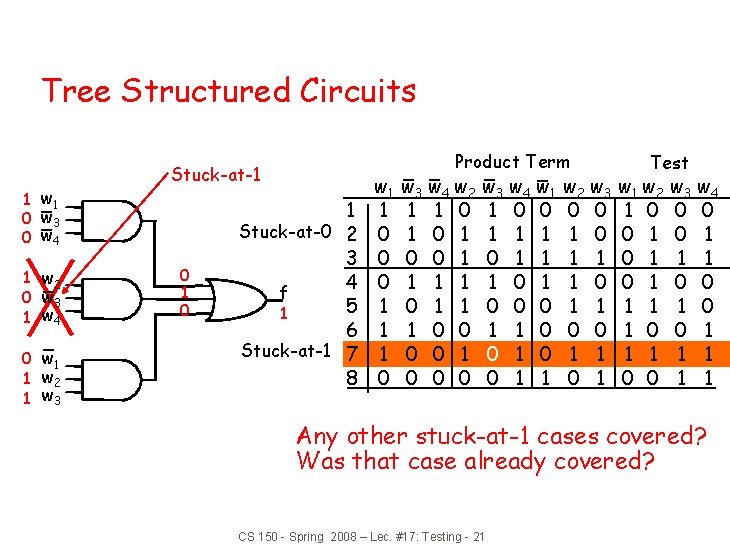
Tree Structured Circuits 1 w 1 0 w 3 0 w 4 1 w 2 0 w 3 1 w 4 0 w 1 1 w 2 1 w 3 Stuck-at-1 0 1 Stuck-at-0 2 3 4 f 5 1 6 Stuck-at-1 7 8 w 1 1 0 0 0 1 1 1 0 Product Term w 3 w 4 w 2 1 1 0 1 0 0 1 1 1 0 0 0 w 3 w 4 w 1 1 0 0 1 1 1 0 1 0 0 0 1 1 w 2 w 3 0 0 1 1 1 0 0 1 1 0 1 Test w 1 w 2 1 0 0 1 0 1 1 0 0 w 3 w 4 0 0 0 1 1 1 Any other stuck-at-1 cases covered? Was that case already covered? CS 150 - Spring 2008 – Lec. #17: Testing - 21

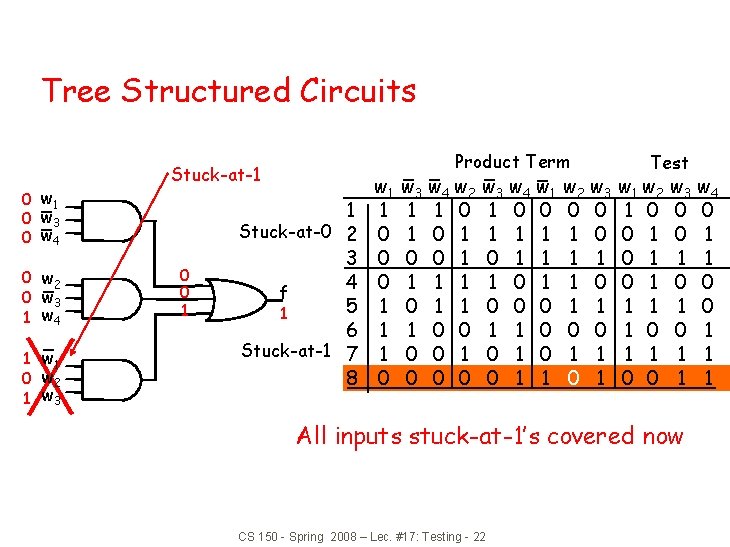
Tree Structured Circuits 0 w 1 0 w 3 0 w 4 0 w 2 0 w 3 1 w 4 1 w 1 0 w 2 1 w 3 Stuck-at-1 0 0 1 1 Stuck-at-0 2 3 4 f 5 1 6 Stuck-at-1 7 8 w 1 1 0 0 0 1 1 1 0 Product Term w 3 w 4 w 2 1 1 0 1 0 0 1 1 1 0 0 0 w 3 w 4 w 1 1 0 0 1 1 1 0 1 0 0 0 1 1 w 2 w 3 0 0 1 1 1 0 0 1 1 0 1 Test w 1 w 2 1 0 0 1 0 1 1 0 0 w 3 w 4 0 0 0 1 1 1 All inputs stuck-at-1’s covered now CS 150 - Spring 2008 – Lec. #17: Testing - 22

Key insight about testing z If a wire is untestable for stuck-at-one (stuck-at-0), there is no difference in behavior from 1 (0) y Therefore: can replace wire with constant power (ground) y Simplify the circuit Test for B s-a-1 requires A=1 & A=0 B cannot be tested for s-a-1 Can eliminate B (set to 1) CS 150 - Spring 2008 – Lec. #17: Testing - 23

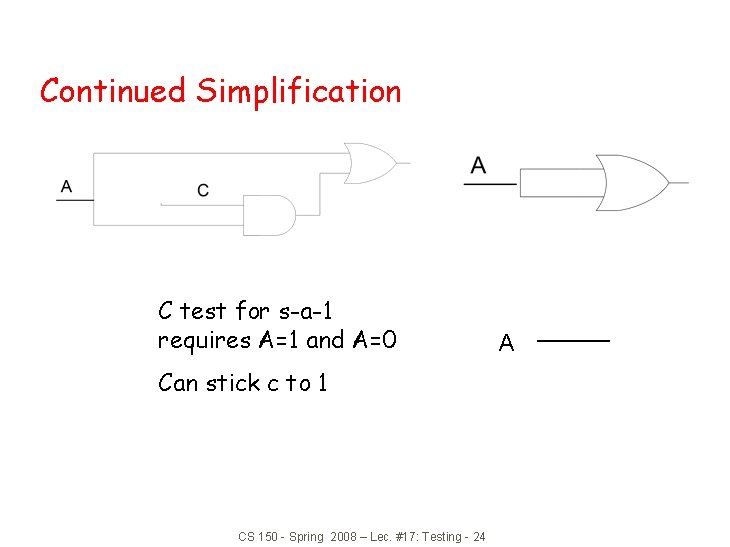
Continued Simplification C test for s-a-1 requires A=1 and A=0 Can stick c to 1 CS 150 - Spring 2008 – Lec. #17: Testing - 24 A

Announcements z Midterm Tuesday y Design-oriented, 5 questions y Open book and notes y All subjects covered in class or text sections fair game CS 150 - Spring 2008 – Lec. #17: Testing - 25

Random Testing z So far: deterministic testing z Alternative: random testing y Generate random input patterns to distinguish between the correct function and the faulty function Probability Fault Detected Small number of tests has reasonable probability of finding the fault Number of Tests CS 150 - Spring 2008 – Lec. #17: Testing - 26

Sequential Testing z Due to embedded state inside flip-flops, it is difficult to employ the same methods as with combinational logic z Alternative approach: design for test y Scan Path technique: FF inputs pass through multiplexer stages to allow them to be used in normal mode as well as a special test shift register mode CS 150 - Spring 2008 – Lec. #17: Testing - 27

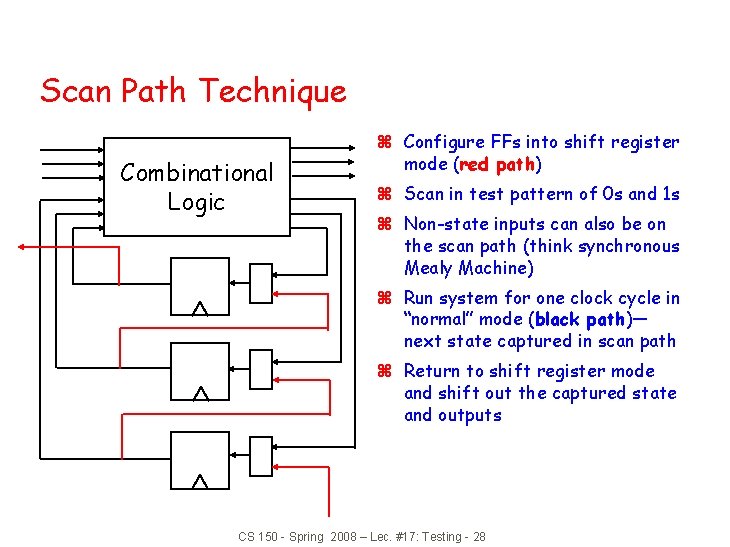
Scan Path Technique Combinational Logic z Configure FFs into shift register mode (red path) z Scan in test pattern of 0 s and 1 s z Non-state inputs can also be on the scan path (think synchronous Mealy Machine) z Run system for one clock cycle in “normal” mode (black path)— next state captured in scan path z Return to shift register mode and shift out the captured state and outputs CS 150 - Spring 2008 – Lec. #17: Testing - 28

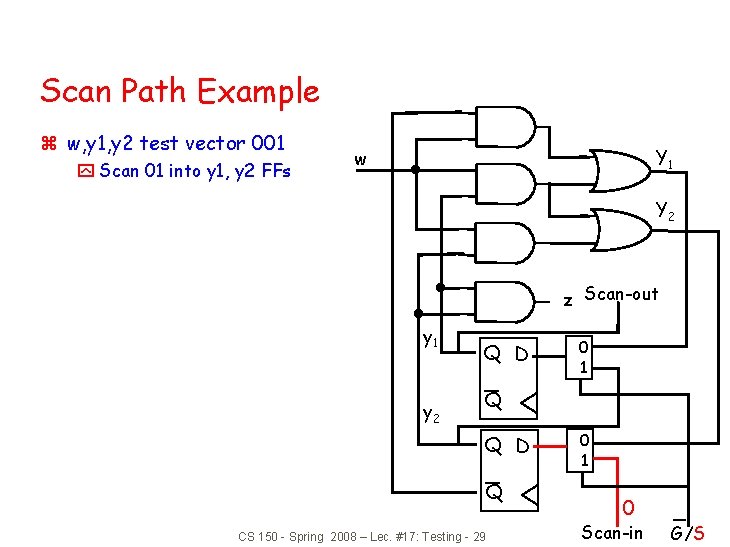
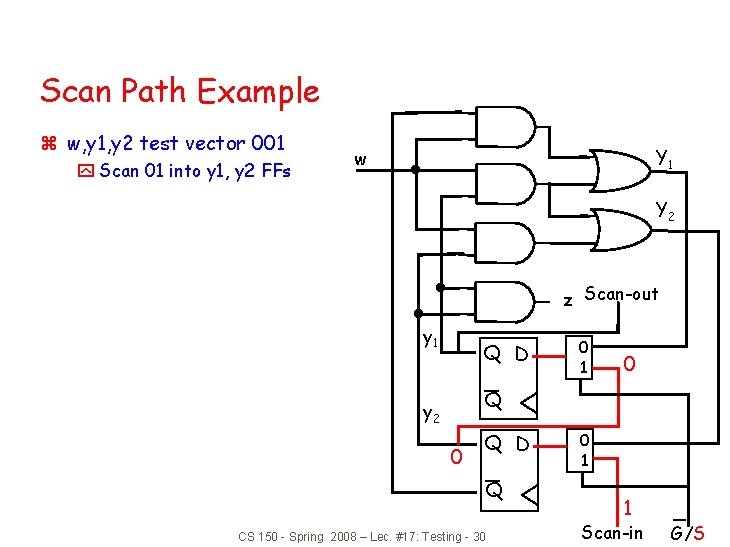
Scan Path Example z w, y 1, y 2 test vector 001 y Scan 01 into y 1, y 2 FFs Y 1 w Y 2 z Scan-out y 1 y 2 Q D 0 1 Q Q D Q CS 150 - Spring 2008 – Lec. #17: Testing - 29 0 1 0 Scan-in G/S

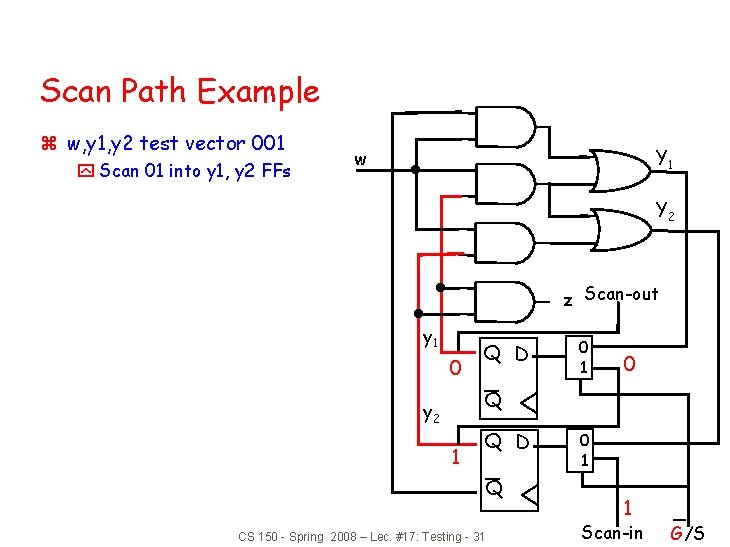
Scan Path Example z w, y 1, y 2 test vector 001 y Scan 01 into y 1, y 2 FFs Y 1 w Y 2 z Scan-out y 1 Q D 0 1 0 Q y 2 0 Q D Q CS 150 - Spring 2008 – Lec. #17: Testing - 30 0 1 1 Scan-in G/S

Scan Path Example z w, y 1, y 2 test vector 001 y Scan 01 into y 1, y 2 FFs Y 1 w Y 2 z Scan-out y 1 0 Q D 0 1 0 Q y 2 1 Q D Q CS 150 - Spring 2008 – Lec. #17: Testing - 31 0 1 1 Scan-in G/S

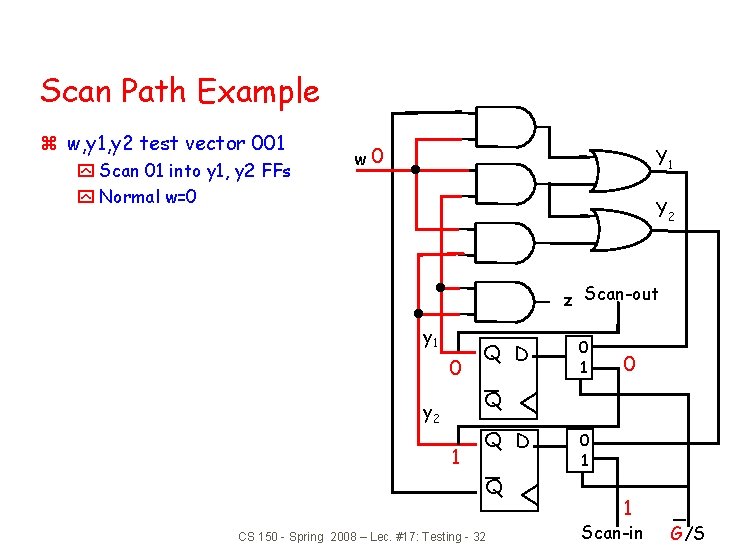
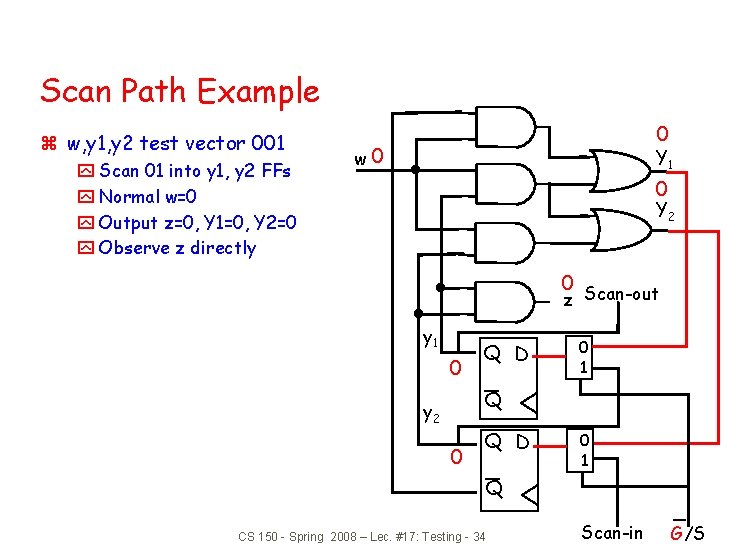
Scan Path Example z w, y 1, y 2 test vector 001 y Scan 01 into y 1, y 2 FFs y Normal w=0 w 0 Y 1 Y 2 z Scan-out y 1 0 Q D 0 1 0 Q y 2 1 Q D Q CS 150 - Spring 2008 – Lec. #17: Testing - 32 0 1 1 Scan-in G/S

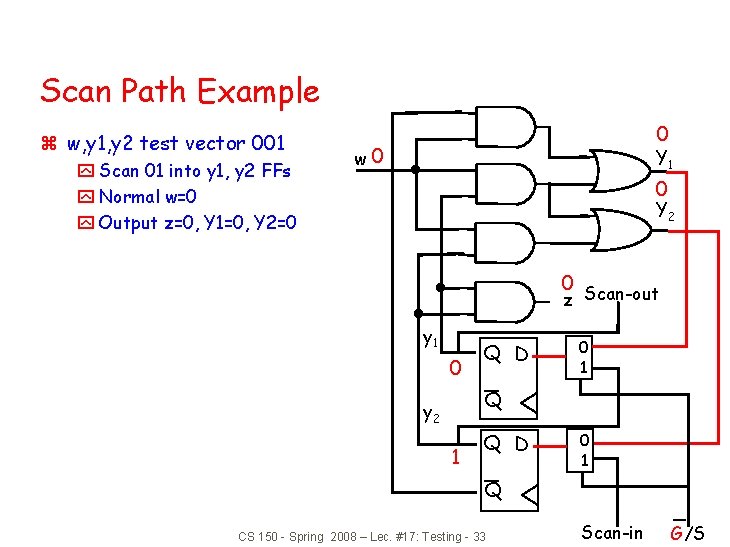
Scan Path Example z w, y 1, y 2 test vector 001 y Scan 01 into y 1, y 2 FFs y Normal w=0 y Output z=0, Y 1=0, Y 2=0 0 w 0 Y 1 0 Y 2 0 z Scan-out y 1 0 Q D 0 1 Q y 2 1 Q D 0 1 Q CS 150 - Spring 2008 – Lec. #17: Testing - 33 Scan-in G/S

Scan Path Example z w, y 1, y 2 test vector 001 y Scan 01 into y 1, y 2 FFs y Normal w=0 y Output z=0, Y 1=0, Y 2=0 y Observe z directly 0 w 0 Y 1 0 Y 2 0 z Scan-out y 1 0 Q D 0 1 Q y 2 0 Q D 0 1 Q CS 150 - Spring 2008 – Lec. #17: Testing - 34 Scan-in G/S

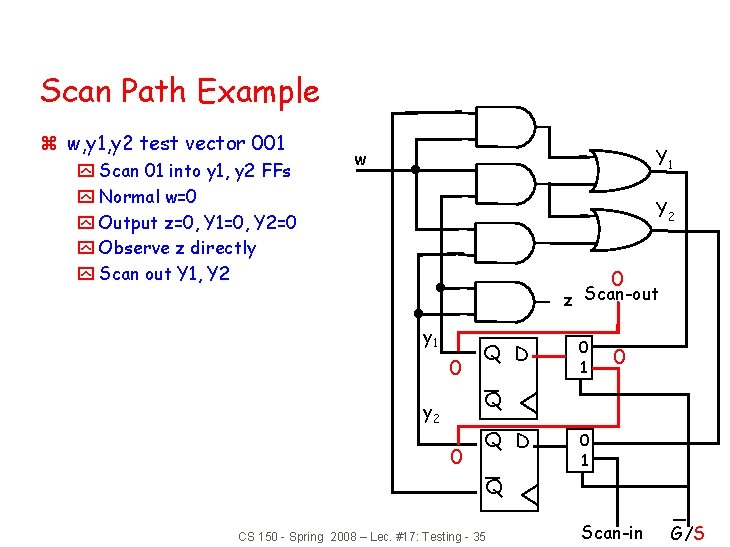
Scan Path Example z w, y 1, y 2 test vector 001 y Scan 01 into y 1, y 2 FFs y Normal w=0 y Output z=0, Y 1=0, Y 2=0 y Observe z directly y Scan out Y 1, Y 2 Y 1 w Y 2 0 z Scan-out y 1 0 Q D 0 1 0 Q y 2 0 Q D 0 1 Q CS 150 - Spring 2008 – Lec. #17: Testing - 35 Scan-in G/S

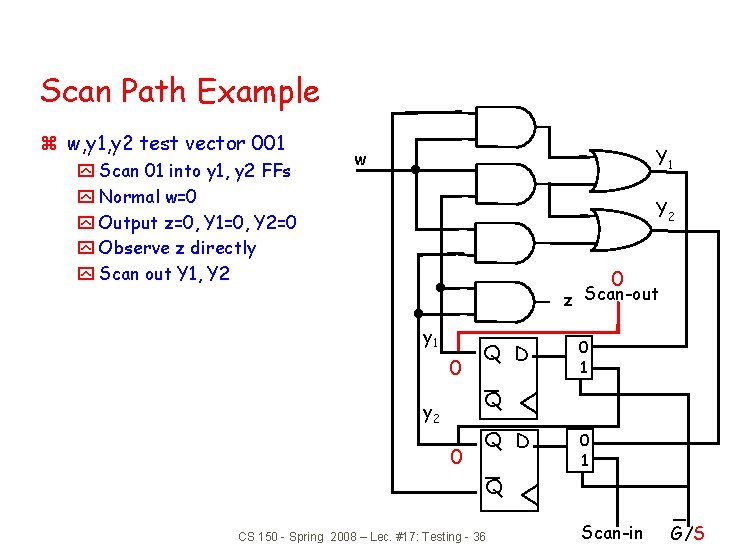
Scan Path Example z w, y 1, y 2 test vector 001 y Scan 01 into y 1, y 2 FFs y Normal w=0 y Output z=0, Y 1=0, Y 2=0 y Observe z directly y Scan out Y 1, Y 2 Y 1 w Y 2 0 z Scan-out y 1 0 Q D 0 1 Q y 2 0 Q D 0 1 Q CS 150 - Spring 2008 – Lec. #17: Testing - 36 Scan-in G/S

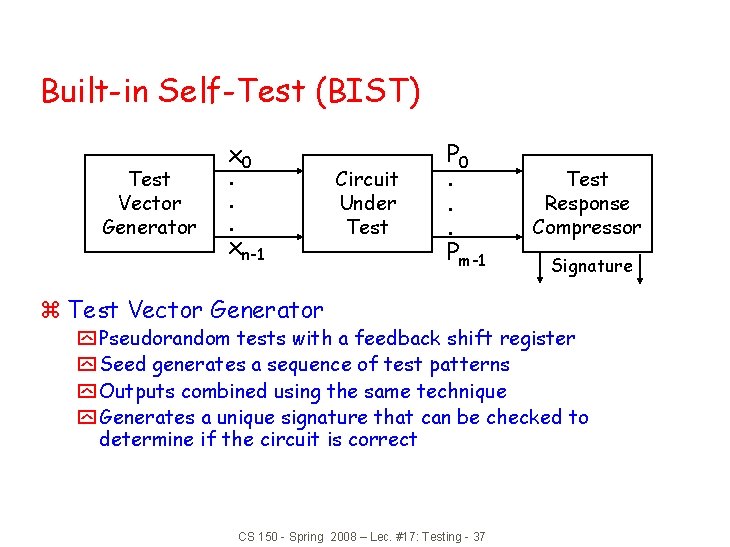
Built-in Self-Test (BIST) Test Vector Generator x 0. . . xn-1 Circuit Under Test P 0. . . Pm-1 z Test Vector Generator Test Response Compressor Signature y Pseudorandom tests with a feedback shift register y Seed generates a sequence of test patterns y Outputs combined using the same technique y Generates a unique signature that can be checked to determine if the circuit is correct CS 150 - Spring 2008 – Lec. #17: Testing - 37

Pseudo-Random Testing z Start with deterministic (known) seed z Apply rotation modulo a large group y Generates a “random” number x Xn+1 = a Xn + b (mod m) y “Anyone who uses arithmetic methods to produce random numbers is in a state of sin” – von Neumann y He invented the technique! z From the point of view of testing, two major advantages y “Statistical” randomness: covers input space y Determinism: always get the same sequence with same seed z Therefore: y Push seed into simulator y Generate signature y Do the same with the circuit y Compare CS 150 - Spring 2008 – Lec. #17: Testing - 38

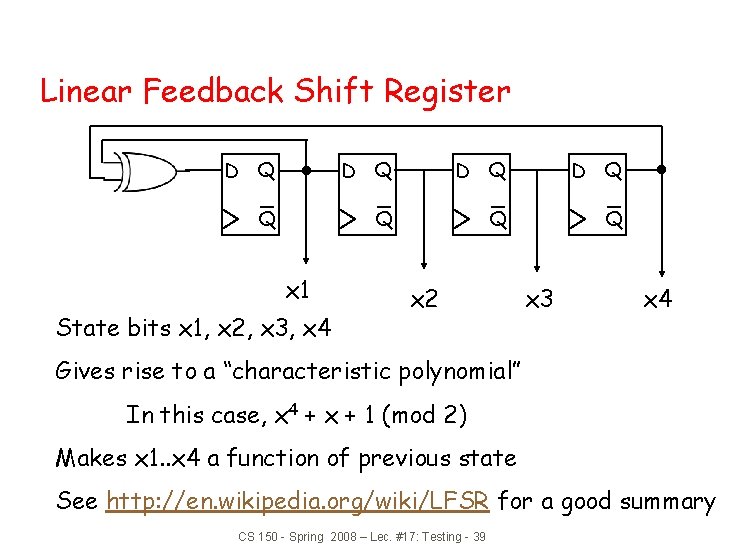
Linear Feedback Shift Register D Q D Q Q Q x 1 State bits x 1, x 2, x 3, x 4 x 2 x 3 x 4 Gives rise to a “characteristic polynomial” In this case, x 4 + x + 1 (mod 2) Makes x 1. . x 4 a function of previous state See http: //en. wikipedia. org/wiki/LFSR for a good summary CS 150 - Spring 2008 – Lec. #17: Testing - 39

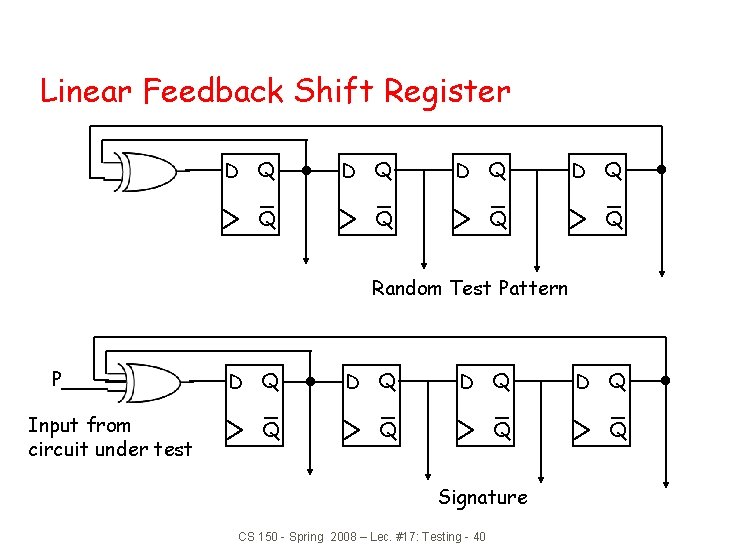
Linear Feedback Shift Register D Q D Q Q Q Random Test Pattern P Input from circuit under test D Q D Q Q Q Signature CS 150 - Spring 2008 – Lec. #17: Testing - 40

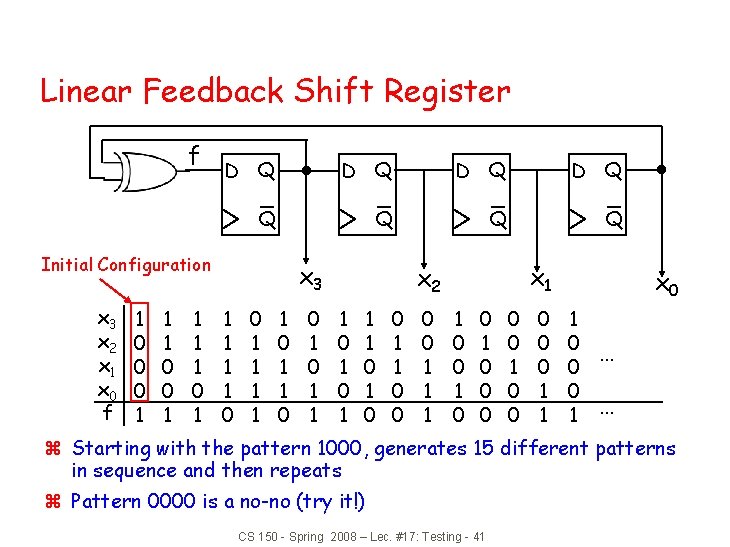
Linear Feedback Shift Register f D Q D Q Q Q Initial Configuration x 3 x 2 x 1 x 0 f 1 0 0 0 1 1 1 1 0 1 x 3 1 1 0 0 1 1 1 0 0 1 1 x 2 1 0 1 1 1 0 0 x 1 0 0 0 1 0 1 1 0 0 0 1 x 0 1 0 0 0 1 … … z Starting with the pattern 1000, generates 15 different patterns in sequence and then repeats z Pattern 0000 is a no-no (try it!) CS 150 - Spring 2008 – Lec. #17: Testing - 41

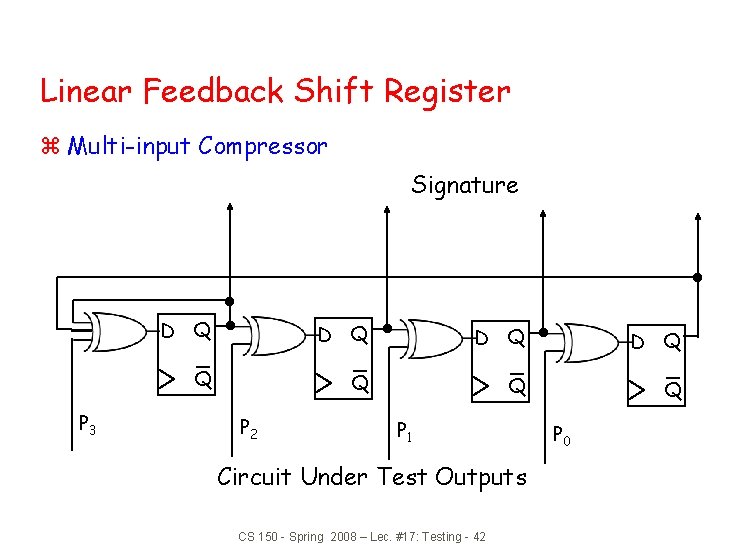
Linear Feedback Shift Register z Multi-input Compressor Signature P 3 D Q D Q Q Q P 2 P 1 Circuit Under Test Outputs CS 150 - Spring 2008 – Lec. #17: Testing - 42 P 0

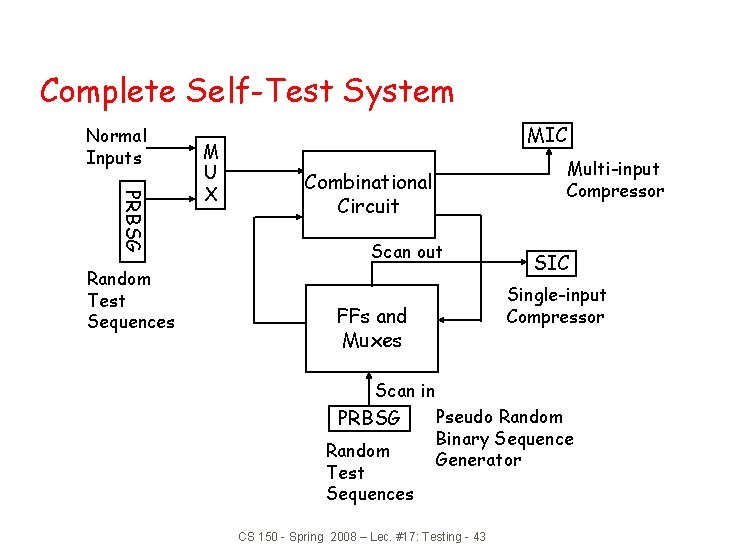
Complete Self-Test System Normal Inputs PRBSG Random Test Sequences M U X MIC Multi-input Compressor Combinational Circuit Scan out SIC Single-input Compressor FFs and Muxes Scan in PRBSG Random Test Sequences Pseudo Random Binary Sequence Generator CS 150 - Spring 2008 – Lec. #17: Testing - 43

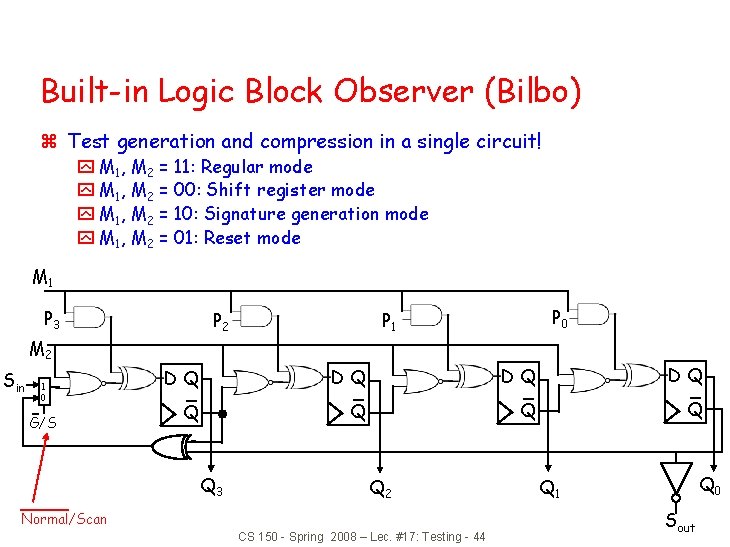
Built-in Logic Block Observer (Bilbo) z Test generation and compression in a single circuit! y M 1, M 2 = 11: Regular mode y M 1, M 2 = 00: Shift register mode y M 1, M 2 = 10: Signature generation mode y M 1, M 2 = 01: Reset mode M 1 P 3 P 2 P 0 P 1 M 2 Sin 1 0 G/S DQ DQ Q Q Q 3 Q 2 Normal/Scan CS 150 - Spring 2008 – Lec. #17: Testing - 44 Q 0 Q 1 Sout

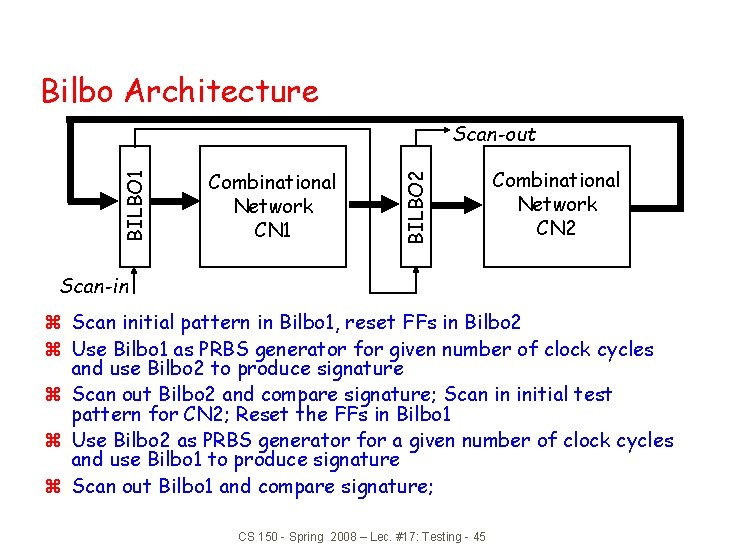
Bilbo Architecture Combinational Network CN 1 BILBO 2 BILBO 1 Scan-out Combinational Network CN 2 Scan-in z Scan initial pattern in Bilbo 1, reset FFs in Bilbo 2 z Use Bilbo 1 as PRBS generator for given number of clock cycles and use Bilbo 2 to produce signature z Scan out Bilbo 2 and compare signature; Scan in initial test pattern for CN 2; Reset the FFs in Bilbo 1 z Use Bilbo 2 as PRBS generator for a given number of clock cycles and use Bilbo 1 to produce signature z Scan out Bilbo 1 and compare signature; CS 150 - Spring 2008 – Lec. #17: Testing - 45

Summary z Fault models y Approach for determining how to develop a test pattern sequence y Weakness is the single fault assumption z Scan Path y Technique for applying test inputs deep within the system, usually for asserting state y Technique for getting internal state to edges of circuit for observation z Built-in Test y Founded on the approach of random testing y Generate pseudo random sequences; compute signature; determine if signature generated is same as signature of a correctly working circuity CS 150 - Spring 2008 – Lec. #17: Testing - 46