Testing Lexicographic Semi Order Models Generalizing the Priority

























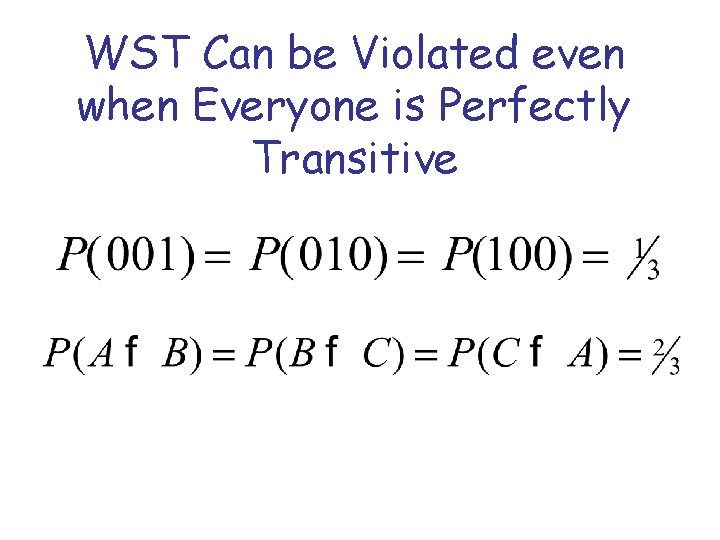


- Slides: 38

Testing Lexicographic Semi. Order Models: Generalizing the Priority Heuristic Michael H. Birnbaum California State University, Fullerton

Outline • Priority Heuristic for risky decisions • New Critical Tests: Allow each person to have a different LS with different parameters • Results for three tests: Interaction, Integration, and Transitivity. • Discussion and questions

Priority Heuristic • Brandstätter, Gigerenzer, & Hertwig • Consider one dimension at a time. • If that “reason” is decisive, other reasons not considered. No integration; no interactions. • Very different from utility models. • Very similar to CPT.

Priority Heuristic • Brandstätter, et al (2006) model assumes people do NOT weight or integrate information. • Each decision based on one dimension only. • Only 4 dimensions considered. • Order fixed: L, P(L), H, P(H).

PH for 2 -branch gambles • First: minimal gains. If the difference exceeds 1/10 the (rounded) maximal gain, choose by best minimal gain. • If minimal gains not decisive, consider probability; if difference exceeds 1/10, choose best probability. • Otherwise, choose gamble with the best highest consequence.

Priority Heuristic examples A: . 5 to win $100. 5 to win $0 B: $40 for sure Reason: lowest consequence. C: . 02 to win $100. 98 to win $0 Reason: highest consequence. D: $4 for sure

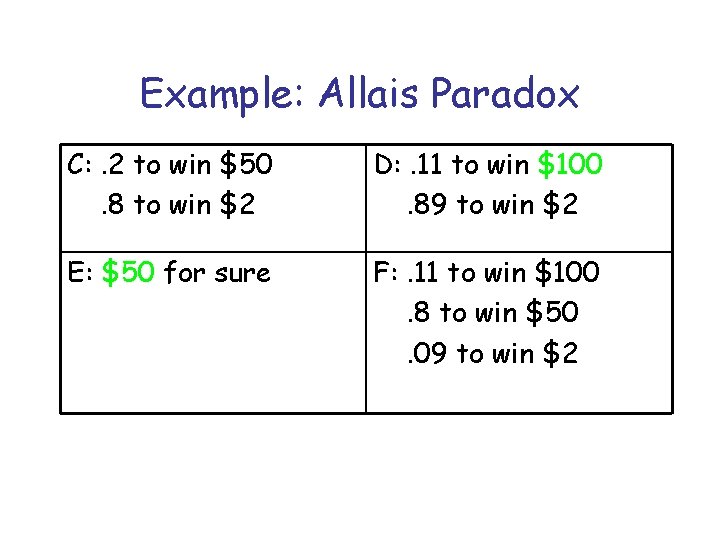
Example: Allais Paradox C: . 2 to win $50. 8 to win $2 D: . 11 to win $100. 89 to win $2 E: $50 for sure F: . 11 to win $100. 8 to win $50. 09 to win $2

PH Reproduces Some Data… Predicts 100% of modal choices in Kahneman & Tversky, 1979. Predicts 85% of choices in Erev, et al. (1992) Predicts 73% of Mellers, et al. (1992) data

…But not all Data • • Birnbaum & Navarrete (1998): 43% Birnbaum (1999): 25% Birnbaum (2004): 23% Birnbaum & Gutierrez (in press): 30%

Problems • No attention to middle branch, contrary to results in Birnbaum (1999) • Fails to predict stochastic dominance in cases where people satisfy it in Birnbaum (1999). Fails to predict violations when 70% violate stochastic dominance. • Not accurate when EVs differ. • No individual differences and no free parameters. Different data sets have different parameters. Delta >. 12 & Delta <. 04.

Modifications: • People act as if they compute ratio of EV and choose higher EV when ratio > 2. • People act as if they can detect stochastic dominance. • Although these help, they do not improve model to more than 50% accuracy. • Today: Suppose different people have different LS with different parameters.

Family of LS • In two-branch gambles, G = (x, p; y), there are three dimensions: L = lowest outcome (y), P = probability (p), and H = highest outcome (x). • There are 6 orders in which one might consider the dimensions: LPH, LHP, PLH, PHL, HPL, HLP. • In addition, there are two threshold parameters (for the first two dimensions).

New Tests of Independence • Dimension Interaction: Decision should be independent of any dimension that has the same value in both alternatives. • Dimension Integration: indecisive differences cannot add up to be decisive. • Priority Dominance: if a difference is decisive, no effect of other dimensions.

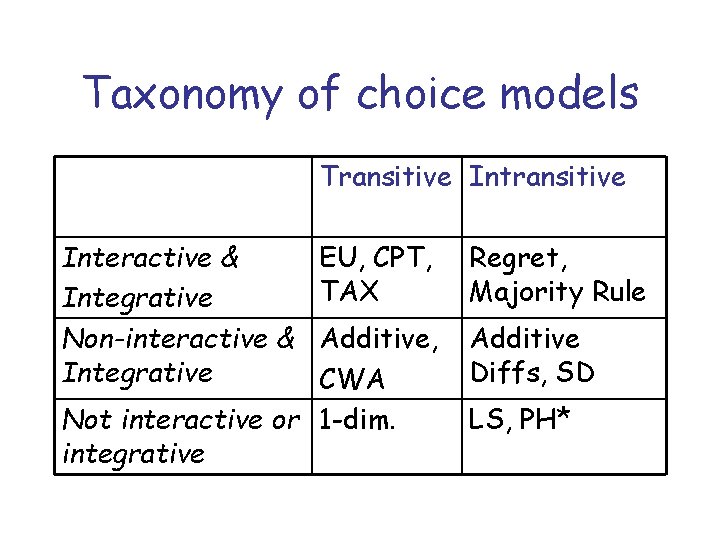
Taxonomy of choice models Transitive Interactive & Integrative Non-interactive & Integrative EU, CPT, TAX Additive, CWA Not interactive or 1 -dim. integrative Regret, Majority Rule Additive Diffs, SD LS, PH*

Testing Algebraic Models with Error-Filled Data • Models assume or imply formal properties such as interactive independence. • But these properties may not hold if data contain “error. ” • Different people might have different “true” preference orders, and different items might produce different amounts of error.

Error Model Assumptions • Each choice pattern in an experiment has a true probability, p, and each choice has an error rate, e. • The error rate is estimated from inconsistency of response to the same choice by same person over repetitions.

Priority Heuristic Implies • Violations of Transitivity • Satisfies Interactive Independence: Decision cannot be altered by any dimension that is the same in both gambles. • No Dimension Integration: 4 -choice property. • Priority Dominance. Decision based on dimension with priority cannot be overruled by changes on other dimensions. 6 -choice.

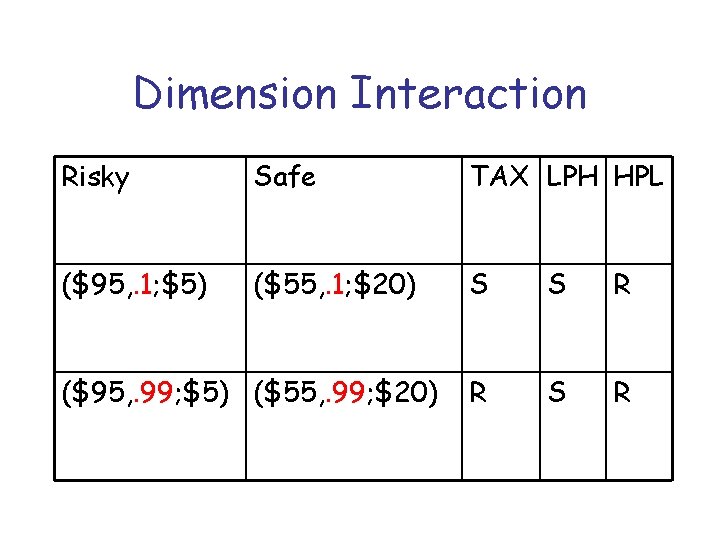
Dimension Interaction Risky Safe TAX LPH HPL ($95, . 1; $5) ($55, . 1; $20) S S R R S R ($95, . 99; $5) ($55, . 99; $20)

Family of LS • 6 Orders: LPH, LHP, PLH, PHL, HPL, HLP. • There are 3 ranges for each of two parameters, making 9 combinations of parameter ranges. • There are 6 X 9 = 54 LS models. • But all models predict SS, RR, or ? ? .

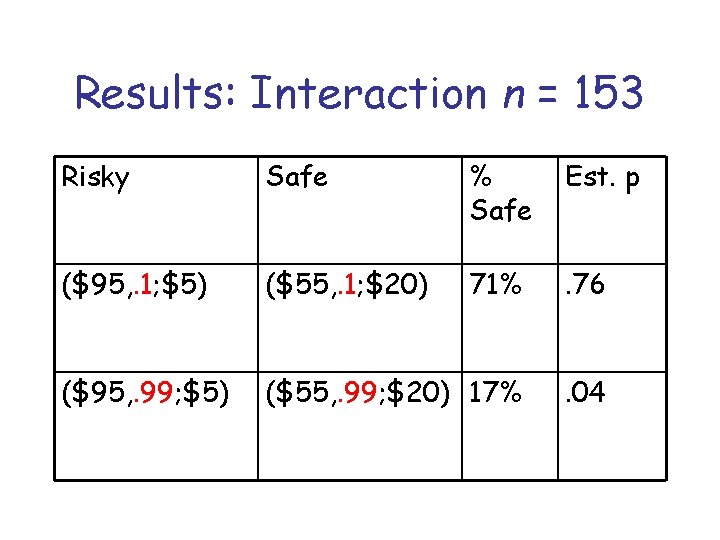
Results: Interaction n = 153 Risky Safe % Safe Est. p ($95, . 1; $5) ($55, . 1; $20) 71% . 76 ($95, . 99; $5) ($55, . 99; $20) 17% . 04

Analysis of Interaction • • • Estimated probabilities: P(SS) = 0 (prior PH) P(SR) = 0. 75 (prior TAX) P(RS) = 0 P(RR) = 0. 25 Priority Heuristic: Predicts SS

Probability Mixture Model • Suppose each person uses a LS on any trial, but randomly switches from one order to another and one set of parameters to another. • But any mixture of LS is a mix of SS, RR, and ? ? . So no LS mixture model explains SR or RS.

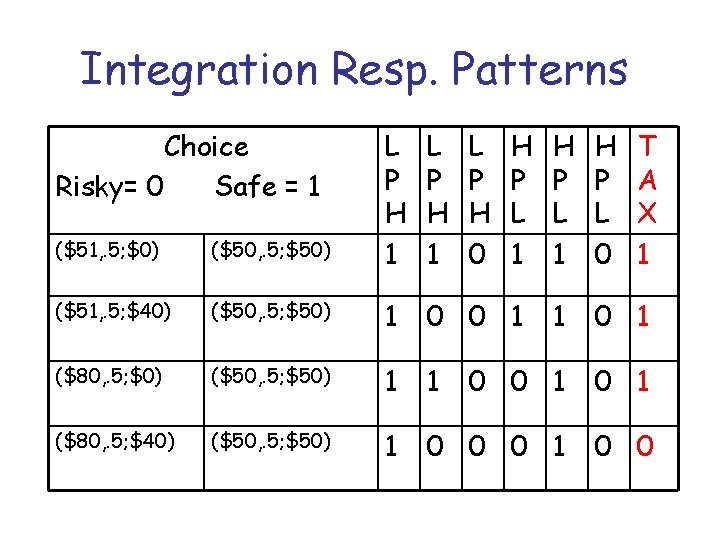
Dimension Integration Study with Adam La. Croix • Difference produced by one dimension cannot be overcome by integrating nondecisive differences on 2 dimensions. • We can examine all six LS Rules for each experiment X 9 parameter combinations. • Each experiment manipulates 2 factors. • A 2 x 2 test yields a 4 -choice property.

Integration Resp. Patterns Choice Risky= 0 Safe = 1 ($51, . 5; $0) ($50, . 5; $50) L P H 1 L P H 0 H P L 1 H P L 0 T A X 1 ($51, . 5; $40) ($50, . 5; $50) 1 0 0 1 1 0 1 ($80, . 5; $0) ($50, . 5; $50) 1 1 0 0 1 ($80, . 5; $40) ($50, . 5; $50) 1 0 0 0 1 0 0

54 LS Models • Predict SSSS, SRSR, SSRR, or RRRR. • TAX predicts SSSR—two improvements to R can combine to shift preference. • Mixture model of LS does not predict SSSR pattern.

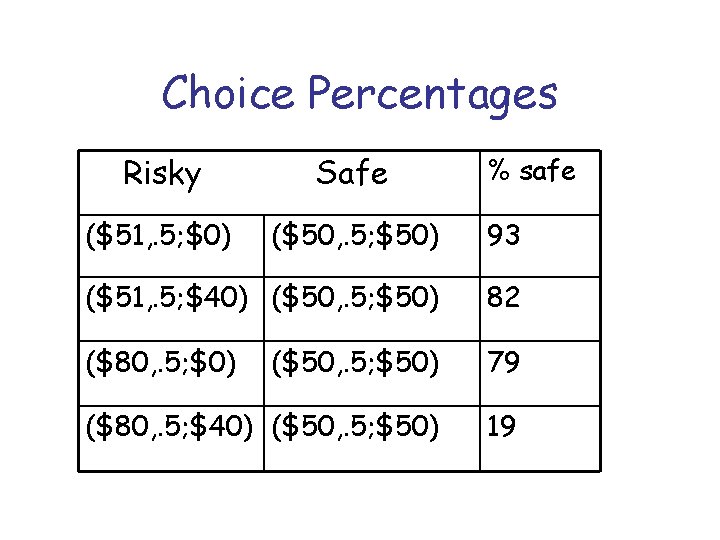
Choice Percentages Risky Safe ($51, . 5; $0) ($50, . 5; $50) 93 ($51, . 5; $40) ($50, . 5; $50) 82 ($80, . 5; $0) ($50, . 5; $50) 79 ($80, . 5; $40) ($50, . 5; $50) 19 % safe

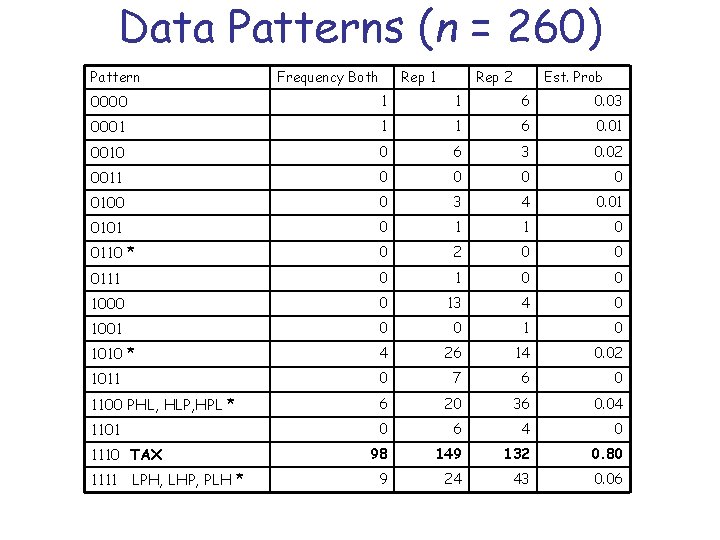
Test of Dim. Integration • Data form a 16 X 16 array of response patterns to four choice problems with 2 replicates. • Data are partitioned into 16 patterns that are repeated in both replicates and frequency of each pattern in one or the other replicate but not both.

Data Patterns (n = 260) Pattern Frequency Both Rep 1 Rep 2 Est. Prob 0000 1 1 6 0. 03 0001 1 1 6 0. 01 0010 0 6 3 0. 02 0011 0 0 0100 0 3 4 0. 01 0101 0 1 1 0 0110 * 0 2 0 0 0111 0 0 1000 0 13 4 0 1001 0 0 1010 * 4 26 14 0. 02 1011 0 7 6 0 1100 PHL, HLP, HPL * 6 20 36 0. 04 1101 0 6 4 0 98 149 132 0. 80 9 24 43 0. 06 1110 TAX 1111 LPH, LHP, PLH *

Results: Dimension Integration • Data strongly violate independence property of LS family • Data are consistent instead with dimension integration. Two small, indecisive effects can combine to reverse preferences. • Replicated with all pairs of 2 dims.

New Studies of Transitivity • LS models violate transitivity: A > B and B > C implies A > C. • Birnbaum & Gutierrez tested transitivity using Tversky’s gambles, but using typical methods for display of choices. • Also used pie displays with and without numerical information about probability. Similar results with both procedures.

Replication of Tversky (‘ 69) with Roman Gutierez • Two studies used Tversky’s 5 gambles, formatted with tickets instead of pie charts. Two conditions used pies. • Exp 1, n = 251. • No pre-selection of participants. • Participants served in other studies, prior to testing (~1 hr).

Three of Tversky’s (1969) Gambles • A = ($5. 00, 0. 29; $0, 0. 79) • C = ($4. 50, 0. 38; $0, 0. 62) • E = ($4. 00, 0. 46; $0, 0. 54) Priority Heurisitc Predicts: A preferred to C; C preferred to E, But E preferred to A. Intransitive. TAX (prior): E > C > A

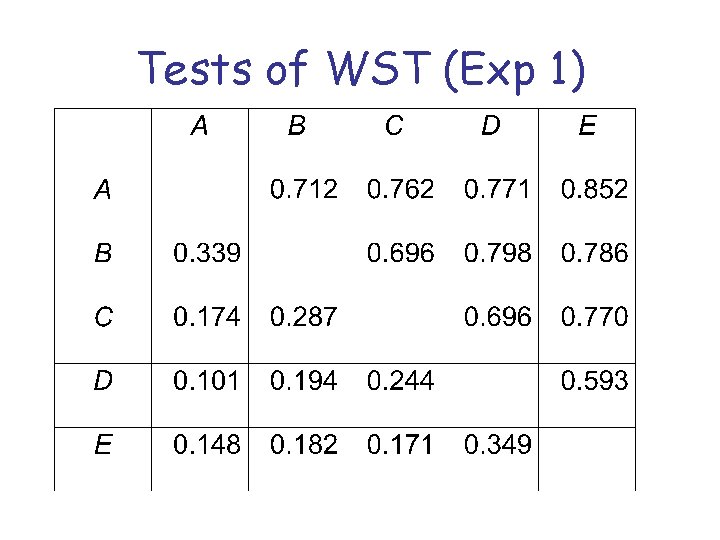
Tests of WST (Exp 1)

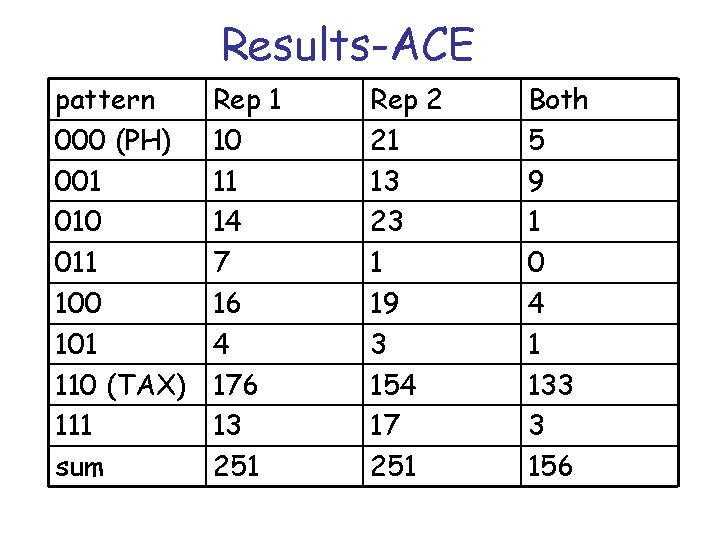
Response Combinations Notation 000 001 010 011 100 101 110 111 (A, C) A A C C (C, E) C C E E (E, A) E A E A * PH TAX *
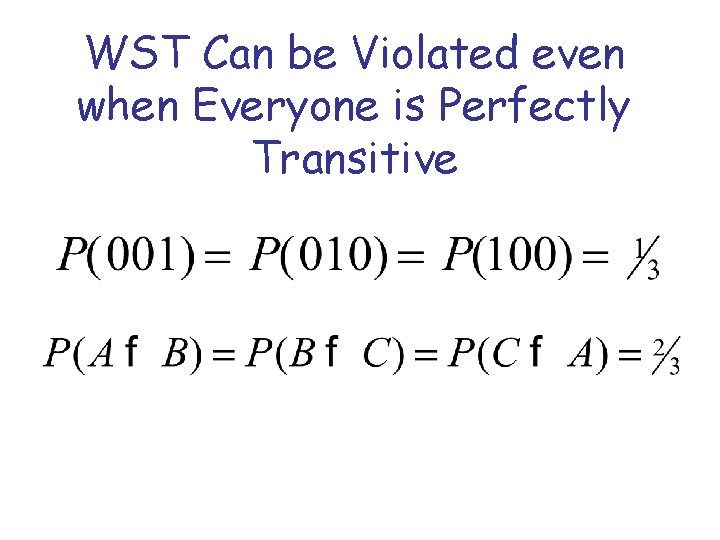
WST Can be Violated even when Everyone is Perfectly Transitive

Results-ACE pattern 000 (PH) 001 010 011 100 101 110 (TAX) 111 sum Rep 1 10 11 14 7 16 4 176 13 251 Rep 2 21 13 23 1 19 3 154 17 251 Both 5 9 1 0 4 1 133 3 156

Comments • Results were surprisingly transitive, unlike Tversky’s data. • Differences: no pre-test, selection; • Probability represented by # of tickets (100 per urn); similar results with pies. • Participants have practice with variety of gambles, & choices; • Tested via Computer.

Summary • Priority Heuristic model’s predicted violations of transitivity are rare. • Dimension Interaction violates any member of LS models including PH. • Dimension Integration violates any LS model including PH. • Data violate mixture model of LS. • Evidence of Interaction and Integration compatible with models like EU, CPT, TAX.