Testing Composite Higgs Models at the Higgs Factory

Testing Composite Higgs Models at the Higgs Factory Kei Yagyu (Osaka U. ) Collaboration with S. De Curtis, L. Delle Rose (Florence U. ) and S. Moretti (Southampton U. ) 1810. 06465 (JHEP), 1803. 01865 (PLB) LCWS 2019, Oct. 30 th, Sendai

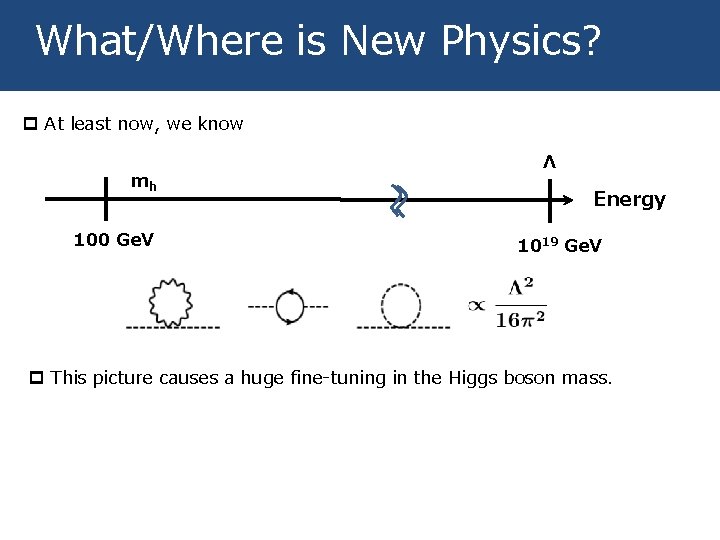
What/Where is New Physics? p At least now, we know mh 100 Ge. V Λ Energy 1019 Ge. V p This picture causes a huge fine-tuning in the Higgs boson mass.

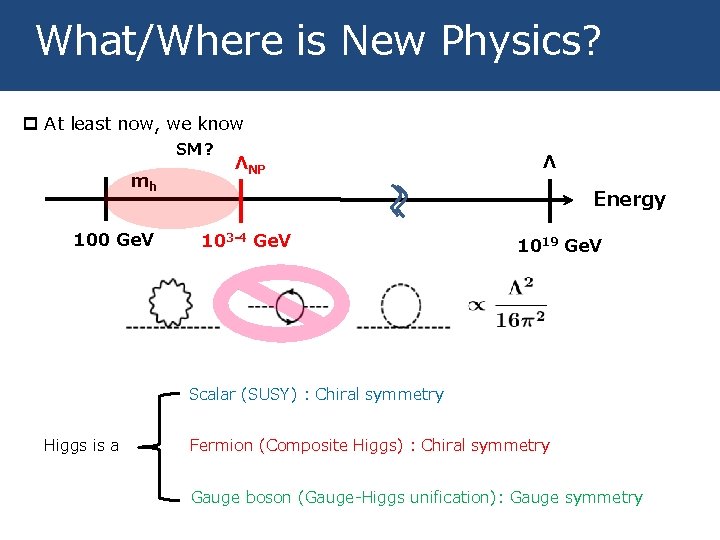
What/Where is New Physics? p At least now, we know SM？ mh 100 Ge. V ΛNP Λ Energy 103 -4 Ge. V 1019 Ge. V Scalar (SUSY) : Chiral symmetry Higgs is a Fermion (Composite Higgs) : Chiral symmetry Gauge boson (Gauge-Higgs unification): Gauge symmetry

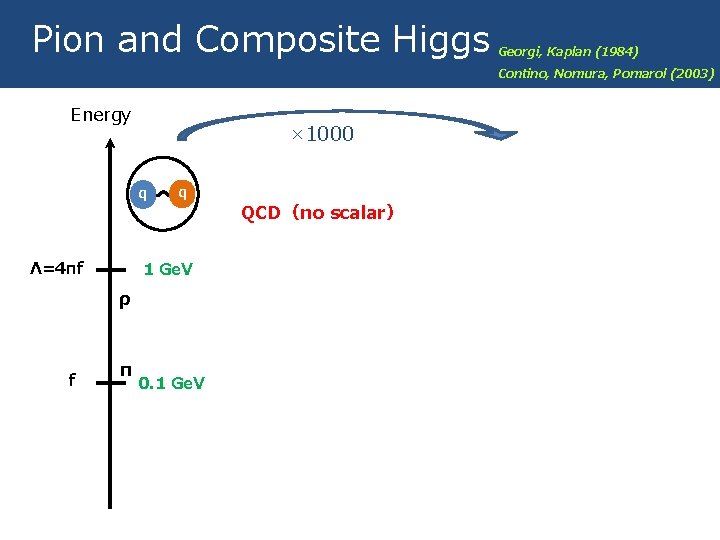
Pion and Composite Higgs Energy q Λ=4πf q 1 Ge. V QCD（no scalar） G = SU(2)L × SU(2)R ρ Non-pert. effects f π 0. 1 Ge. V H = SU(2)V 9/35 Georgi, Kaplan (1984) Contino, Nomura, Pomarol (2003)

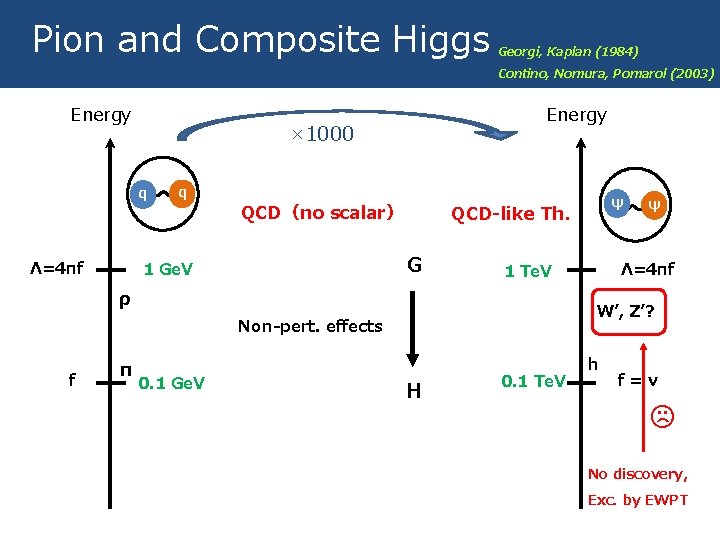
Pion and Composite Higgs Energy × 1000 q Λ=4πf q 1 Ge. V ρ f π 0. 1 Ge. V QCD（no scalar） 9/35 Georgi, Kaplan (1984) Contino, Nomura, Pomarol (2003)

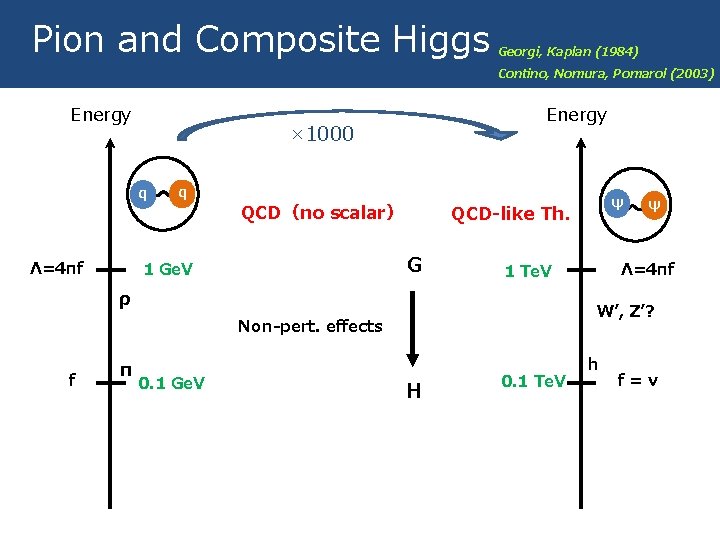
Pion and Composite Higgs Energy Λ=4πf q QCD（no scalar） Contino, Nomura, Pomarol (2003) W’, Z’? Non-pert. effects f 0. 1 Ge. V ψ Λ=4πf 1 Te. V ρ π ψ QCD-like Th. G 1 Ge. V Georgi, Kaplan (1984) Energy × 1000 q 9/35 H 0. 1 Te. V h f=v

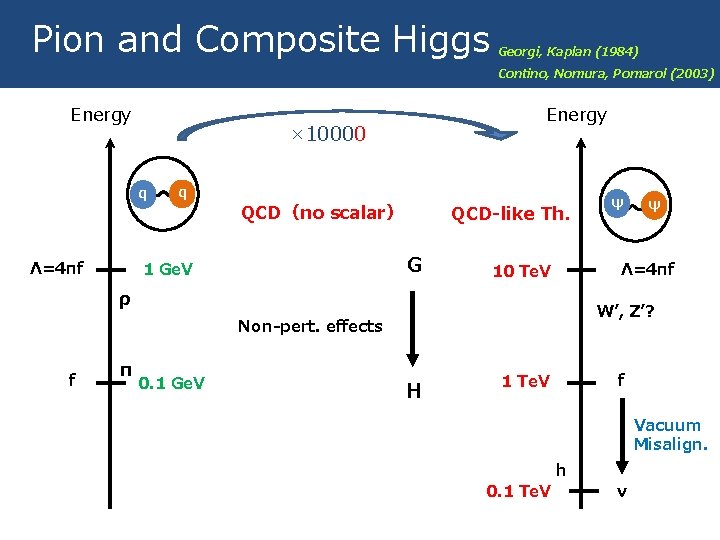
Pion and Composite Higgs Energy Λ=4πf q QCD（no scalar） Contino, Nomura, Pomarol (2003) W’, Z’? Non-pert. effects f 0. 1 Ge. V ψ Λ=4πf 1 Te. V ρ π ψ QCD-like Th. G 1 Ge. V Georgi, Kaplan (1984) Energy × 1000 q 9/35 H 0. 1 Te. V h f=v ☹ No discovery, Exc. by EWPT

Pion and Composite Higgs Energy q G W’, Z’? Heavy enough H ψ Λ=4πf 10 Te. V ☺ Non-pert. effects 0. 1 Ge. V ψ QCD-like Th. ρ f Contino, Nomura, Pomarol (2003) Energy QCD（no scalar） 1 Ge. V π Georgi, Kaplan (1984) × 10000 q Λ=4πf 9/35 1 Te. V ☹ Too heavy h f=v Incorrect ☹

Pion and Composite Higgs Energy Λ=4πf q QCD（no scalar） Contino, Nomura, Pomarol (2003) QCD-like Th. G 1 Ge. V Georgi, Kaplan (1984) Energy × 10000 q 9/35 W’, Z’? Non-pert. effects π 0. 1 Ge. V ψ Λ=4πf 10 Te. V ρ f ψ H f 1 Te. V Vacuum Misalign. 0. 1 Te. V h v

16/35 Basic Rules for the Construction p The structure of the Higgs sector is determined by the coset G/H. p H should contain the custodial SO(4) ≃ SU(2)L×SU(2)R symmetry. p The number of NGBs (dim. G-dim. H) must be 4 or lager. p Explicit breaking of G must be introduced. G G [dim] f Mrazek et al, NPB 853 (2011) 1 -48 H [dim] Higgs sector Agashe, Contino, Pomarol (2005) SO(5) [10] SO(4) [6] H SO(6) [15] SO(5) [10] Gsm SO(6) [15] SO(4)×SO(2) [7] SU(5) [24] SU(4)×U(1) [16] Sp(6) [21] Sp(4)×SU(2) [13] SU(5) [24] SO(5) [10] v EM Φ Φ+S Φ + Φ’ Φ+Δ+S etc

Structure of CHMs Elementary Sector Strong Sector Mixing ・Explicit G breaking ・No Higgs ・No potential & Yukawa Partial Compositeness ・Exact G symmetry ・G/H ∋ Σ (p. NGBs) Only kinetic terms Potential = + + + ・・・

Vacuum misalignment p The Higgs potential is written as Stationary condition (V’ = 0)

Vacuum misalignment p The Higgs potential is written as Stationary condition (V’ = 0) Higgs Mass (V’’) The light Higgs boson is naturally explained by an O(1) coefficient. α and β can be predicted from strong dynamics.

Higgs boson mass (Minimal CHM) De Curtis, Redi, Tesi, JHEP 04 (2012) 042 f = 800 Ge. V, mρ = 2. 5 Te. V Lightest extra fermion mass [Ge. V]

Structure of CHMs Elementary Sector Strong Sector Mixing ・Explicit G breaking ・No Higgs ・No potential & Yukawa Only kinetic terms Higgs boson couplings: Partial Compositeness ・Exact G symmetry ・G/H ∋ Φ (p. NGBs)

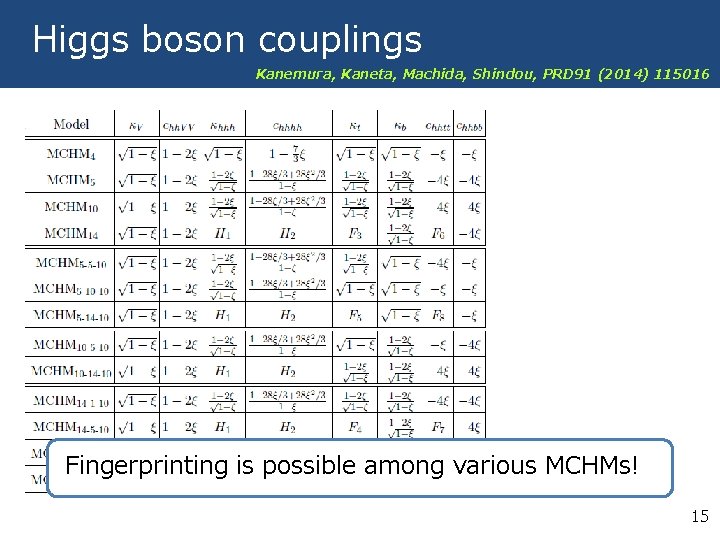
Higgs boson couplings Kanemura, Kaneta, Machida, Shindou, PRD 91 (2014) 115016 Fingerprinting is possible among various MCHMs! 15

Pion and Composite Higgs Energy × 10000 q Λ=4πf q 1 Ge. V QCD（no scalar） 9/35 Georgi, Kaplan (1984) Contino, Nomura, Pomarol (2003) Energy QCD-like Th. π ψ Λ=4πf 10 Te. V ρ f ψ W’, Z’? 0. 1 Ge. V f 1 Te. V 0. 1 Te. V h Vacuum Misalignment v ~ f/4π

Pion and Composite Higgs Energy q π Contino, Nomura, Pomarol (2003) Energy QCD（no scalar） QCD-like Th. 1 Ge. V ρ f Georgi, Kaplan (1984) × 10000 q Λ=4πf 9/35 SO(6)×SO(2) SU(3)V SO(4)×SO(2) ψ Λ=4πf 10 Te. V SU(3)L×SU(3)R ψ W’, Z’? K, K … 0. 1 Ge. V f 1 Te. V H, A, H± 0. 1 Te. V h Vacuum Misalignment v ~ f/4π

Effective Potential + O(Φ 6) All the potential parameters mi 2 and λi are given as a function of strong parameters:

Effective Potential + O(Φ 6) p Fermion loop contributions Hardly-broken Z 2 symmetry Unbroken Z 2 symmetry (Inert 2 HDM)

Typical Prediction of Mass Spectrum E Ψ, ρμ f H±, H, A h ~ 125 Ge. V

Correlation b/w f and m. A De Curtis, Delle Rose, Moretti, KY, ar. Xiv: 1803. 01865 [hep-ph]

Correlation b/w m. A and κV (= gh. VV/gh. VVSM) De Curtis, Delle Rose, Moretti, KY, ar. Xiv: 1803. 01865 [hep-ph] MSSM: Feyn. Higgs v 2. 14. 1

Correlation b/w κV and κt

Summary p CHMs (Higgs = p. NGB) can naturally explain the light Higgs boson. p The Higgs potential is predictable from strong dynamics. p Non-minimal Higgs sectors can also be constructed by taking larger cosets. p C 2 HDMs have slower decoupling property (c. f. MSSM). p Correlation b/w κV and κt can be significantly different in the MCHM 5, C 2 HDM and 2 HDM.

Fujii et al, 1710. 07621 [hep-ph] 1%!!

Setup for C 2 HDM p We introduce SO(6) 6 -plet fermions for the explicit Lagrangian: p Z 2 -like symmetry in the strong sector can be introduced. C 2 symmetry (to avoid FCNCs) C 2 = diag(1, 1, 1, -1) 1. Unbroken case, 2. Spontaneously broken case and 3. Hardly broken case (there is no option for the softly-breaking)

Higgs boson couplings Kanemura, Kaneta, Machida, Shindou, PRD 91 (2014) 115016

f VS tanβ 30/35 De Curtis, Delle Rose, Moretti, KY, ar. Xiv: 1803. 01865 [hep-ph]

Correlation b/w m. A and mass differences

Masses of heavy top partners 34/35 De Curtis, Delle Rose, Moretti, KY, ar. Xiv: 1803. 01865 [hep-ph] C 2 HDM MSSM

Slide from Csaba Csaki 32

Slide from Csaba Csaki 33

S, T parameter Panico, Wulzer, ar. Xiv: 1506. 01961 p Contribution from heavy resonances y. L = ΔL/f , m : lightest fermion partner mass