Testing a Claim about a Proportion Section 7

Testing a Claim about a Proportion Section 7 -5 M A R I O F. T R I O L A Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 1

Assumptions when Testing a Claim about a Population Proportion or Percentage • 1) Binomial experiment conditions are satisfied (Section 4 -3) Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 2

Definitions v. Binomial Experiment 1. The experiment must have a fixed number of trials. 2. The trials must be independent. (The outcome of any individual trial doesn’t affect the probabilities in the other trials. ) 3. Each trial must have all outcomes classified into two categories. 4. The probabilities must remain constant for each trial. Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 3

Assumptions when Testing a Claim about a Population Proportion or Percentage • 1) Binomial experiment conditions are satisfied (Section 4 -3) • 2) np ³ 5 and nq ³ 5, so the binomial distribution of sample proportions can be approximated by a normal distribution with µ = np and s = npq Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 4

Notation n = number of trials Ù p = x/n (sample proportion) p = population proportion (given in the null hypothesis) q=1–p Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 5

Test Statistic for Testing a Claim about a Proportion z= Ù p–p pq n Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 6

Test Statistic for Testing a Claim about a Proportion z= Ù p–p pq n z = xs– µ = x – np = npq x n npq n Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman Ù = ppq– p n 7

Ù p is sometimes given directly “ 10% of the observed sports cars are red” is expressed as Ù p = 0. 10 Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 8

Ù p is sometimes given directly “ 10% of the observed sports cars are red” is expressed as Ù p = 0. 10 Ù p sometimes must be calculated “ 96 surveyed households have cable TV and 54 do not” is calculated as Ù p 96 x =n = = 0. 64 150 (determining the sample proportion of households with cable TV) Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 9

CAUTION Ù When the calculation of p results in a decimal with many places, store the number on your calculator and use all the decimals when evaluating the z test statistic. v v Ù Large errors can result from rounding p too much. Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 10

All three methods 1) Traditional method 2) P-value method 3) Confidence intervals and the testing procedure Step 1 to Step 8 in Section 7 -3 are still valid, except that the test statistic (still the z score by CLT) is calculated using a different formula. Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 11

Example To test a coin is a fair coin or not, John tossed the coin 150 times and recorded total 68 times that the coin landed on tail. Q: Based on the reported result, can we claim it is a fair coin? Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 12

Example Solution Step 1: p = 0. 5 Step 2: p = 0. 5 Step 3: H 0: p = 0. 5 versus H 1: p = 0. 5 Step 4: Select a = 0. 05 (significance level) Step 5: The sample proportion is relevant to this test and its corresponding z-score follows approximately normal distribution (np > 5 and nq > 5, by CLT) Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 13
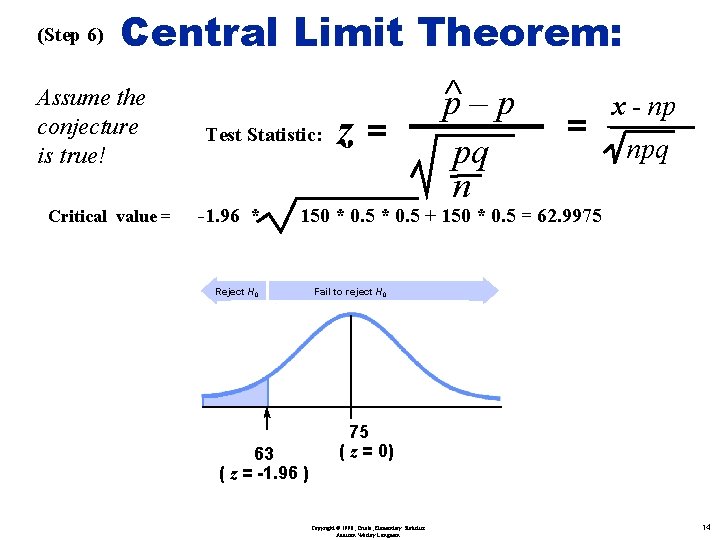
(Step 6) Central Limit Theorem: Assume the conjecture is true! Critical value = Ù Test Statistic: -1. 96 * z= p–p pq n = x - np npq 150 * 0. 5 + 150 * 0. 5 = 62. 9975 Reject H 0 63 ( z = -1. 96 ) Fail to reject H 0 75 ( z = 0) Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 14
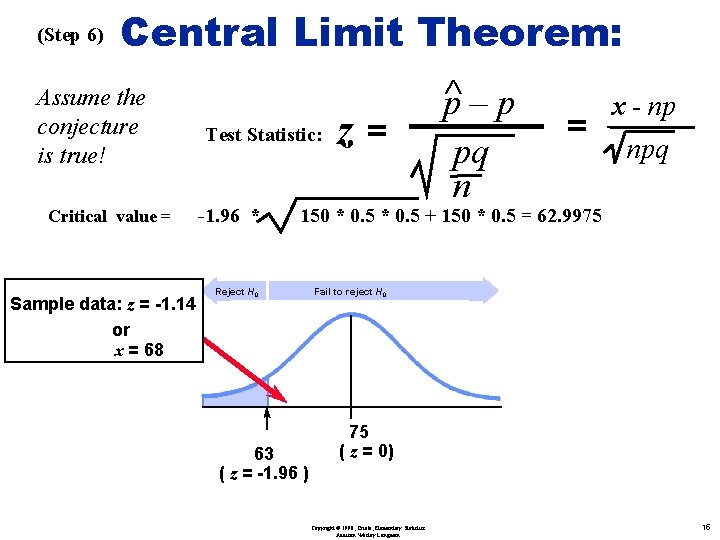
(Step 6) Central Limit Theorem: Assume the conjecture is true! Critical value = Sample data: z = -1. 14 or x = 68 Ù Test Statistic: -1. 96 * z= p–p pq n = x - np npq 150 * 0. 5 + 150 * 0. 5 = 62. 9975 Reject H 0 63 ( z = -1. 96 ) Fail to reject H 0 75 ( z = 0) Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 15

Example Step 8: Conclusion: Based on the reported sample result, there is not enough evidence to rejection of the claim that “the coin is a fair coin”. Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 16
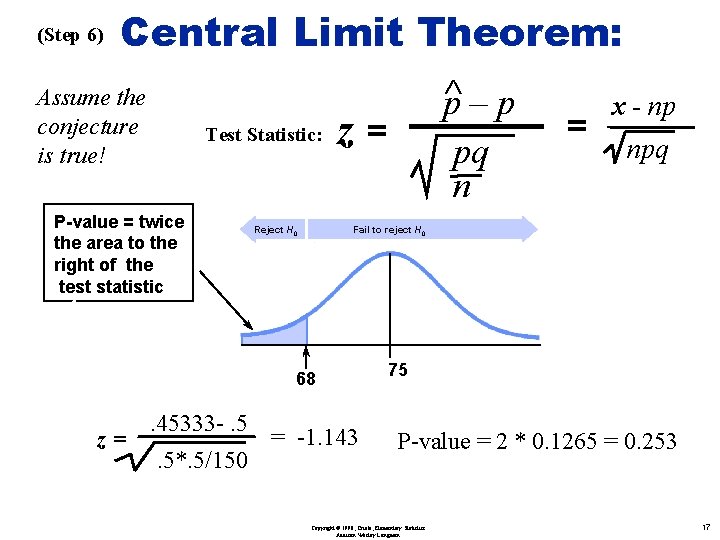
(Step 6) Central Limit Theorem: Ù Assume the conjecture is true! Test Statistic: P-value = twice the area to the right of the test statistic Reject H 0 z= z= . 5*. 5/150 = x - np npq Fail to reject H 0 68 . 45333 -. 5 p–p pq n = -1. 143 75 P-value = 2 * 0. 1265 = 0. 253 Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 17
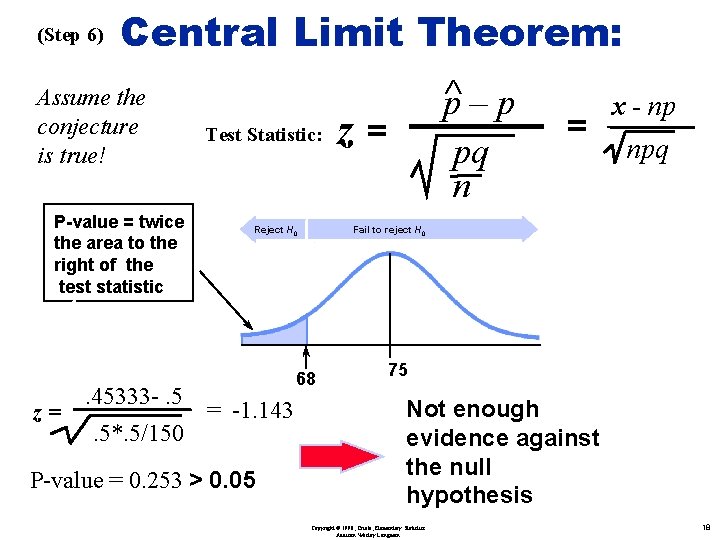
(Step 6) Central Limit Theorem: Assume the conjecture is true! P-value = twice the area to the right of the test statistic z= . 45333 -. 5. 5*. 5/150 Ù Test Statistic: Reject H 0 P-value = 0. 253 > 0. 05 z= = x - np npq Fail to reject H 0 68 = -1. 143 p–p pq n 75 Not enough evidence against the null hypothesis Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 18
- Slides: 18