Testing a Claim about a Mean Large Samples

Testing a Claim about a Mean: Large Samples Section 7 -3 M A R I O F. T R I O L A Copyright © 1998, Triola, Elementary Statistics Copyright© 1998, Triola, Elementary Statistics Addison Longman by. Wesley Addison Wesley Longman 1

For testing a claim about the mean of a single population Assumptions 1) Sample is large (n > 30) a) Central limit theorem applies b) Can use normal distribution 2) Can use sample standard deviation s as estimate for s if s is unknown Copyright© 1998, Triola, Elementary Statistics by Addison Wesley Longman 2

Three Methods Discussed 1) Traditional method 2) P-value method 3) Confidence intervals Note: These three methods are equivalent, I. e. , they will provide the same conclusions. Copyright© 1998, Triola, Elementary Statistics by Addison Wesley Longman 3

Traditional (or Classical) Method of Testing Hypotheses Goal Identify: whether a sample result that is significantly different from the claimed value Copyright© 1998, Triola, Elementary Statistics by Addison Wesley Longman 4

Procedure Figure 7 -4 1. Identify the specific claim or hypothesis to be tested, and put it in symbolic form. 2. Give the symbolic form that must be true when the original claim is false. 3. Of the two symbolic expressions obtained so far, put the one you plan to reject in the null hypothesis H 0 (make the formula with equality). H 1 is the other statement. Or, One simplified rule suggested in the textbook: let null hypothesis H 0 be the one that contains the condition of equality. H 1 is the other statement. Copyright© 1998, Triola, Elementary Statistics by Addison Wesley Longman 5

4. Select the significant level a based on the seriousness of a type I error. Make a small if the consequences of rejecting a true H 0 are severe. The values of 0. 05 and 0. 01 are very common. 5. Identify the statistic that is relevant to this test and its sampling distribution. 6. Determine the test statistic, the critical values, and the critical region. Draw a graph and include the test statistic, critical value(s), and critical region. 7. Reject H 0 if the test statistic is in the critical region. Fail to reject H 0 if the test statistic is not in the critical region. 8. Restate this previous decision in simple non-technical terms. (See Figure 7 -2) Copyright© 1998, Triola, Elementary Statistics by Addison Wesley Longman 6

FIGURE 7 -2 Wording of Conclusions in Hypothesis Tests Original claim is H 0 Do you reject H 0? . No “There is sufficient evidence to warrant (Reject H 0) rejection of the claim that. . . (original claim). ” Yes (Fail to reject H 0) Original claim is H 1 Do you reject H 0? Yes (Reject H 0) No (Fail to reject H 0) Copyright© 1998, Triola, Elementary Statistics by Addison Wesley Longman (This is the only case in which the original claim is rejected). “There is not sufficient evidence to warrant rejection of the claim that. . . (original claim). ” (This is the “The sample data only case in supports the claim that which the. . . (original claim). ” original claim is supported). “There is not sufficient evidence to support the claim that. . . (original claim). ” 7

The traditional (or classical) method of hypothesis testing is actually comparing the sample test statistic value with the critical region value. Copyright© 1998, Triola, Elementary Statistics by Addison Wesley Longman 8

Decision Criterion (Step 7) Reject the null hypothesis if the test statistic is in the critical region Fail to reject the null hypothesis if the test statistic is not in the critical region Copyright© 1998, Triola, Elementary Statistics by Addison Wesley Longman 9

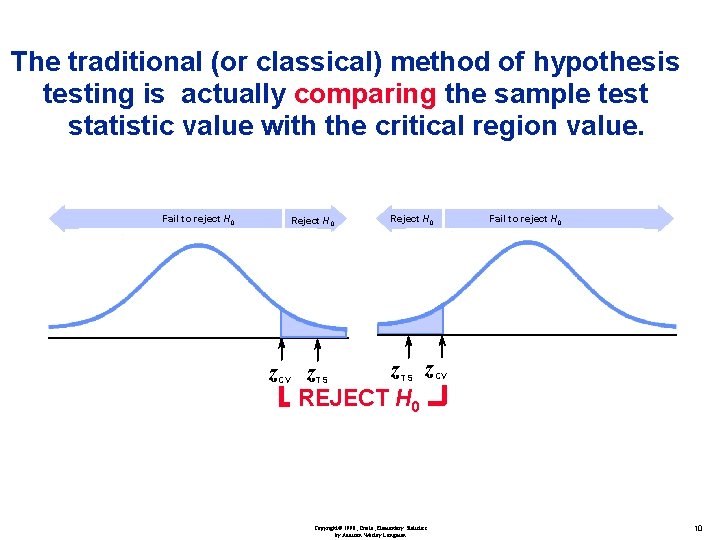
The traditional (or classical) method of hypothesis testing is actually comparing the sample test statistic value with the critical region value. Fail to reject H 0 Reject H 0 z CV Reject H 0 z z z REJECT H 0 TS TS Copyright© 1998, Triola, Elementary Statistics by Addison Wesley Longman Fail to reject H 0 CV 10

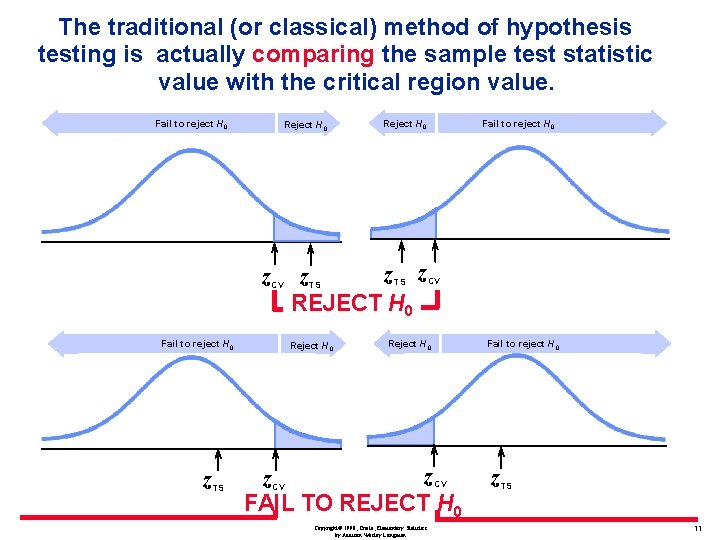
The traditional (or classical) method of hypothesis testing is actually comparing the sample test statistic value with the critical region value. Fail to reject H 0 Reject H 0 z CV Fail to reject H 0 z TS Reject H 0 z z z REJECT H 0 TS Reject H 0 TS Fail to reject H 0 CV Reject H 0 Fail to reject H 0 z z FAIL TO REJECT H 0 CV CV Copyright© 1998, Triola, Elementary Statistics by Addison Wesley Longman z TS 11

Test Statistic for Claims about µ when n > 30 (Step 6) z= x – µx s n Copyright© 1998, Triola, Elementary Statistics by Addison Wesley Longman 12

Example Conjecture: “the average starting salary for a computer science gradate is $30, 000 per year”. For a randomly picked group of 36 computer science graduates, their average starting salary is $36, 100 and the sample standard deviation is $8, 000. Copyright© 1998, Triola, Elementary Statistics by Addison Wesley Longman 13

Example Solution Step 1: µ = 30 k Step 2: µ > 30 k (if believe to be no less than 30 k) Step 3: H 0: µ = 30 k versus H 1: µ > 30 k Step 4: Select a = 0. 05 (significance level) Step 5: The sample mean is relevant to this test and its sampling distribution is approximately normal (n = 36 large, by CLT) Copyright© 1998, Triola, Elementary Statistics by Addison Wesley Longman 14

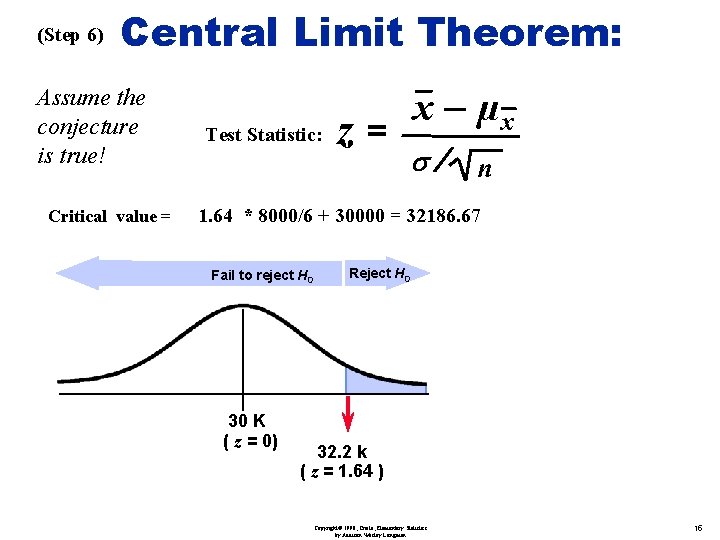
(Step 6) Central Limit Theorem: Assume the conjecture is true! Critical value = Test Statistic: z= x – µx s/ n 1. 64 * 8000/6 + 30000 = 32186. 67 Fail to reject H 0 30 K ( z = 0) Reject H 0 32. 2 k ( z = 1. 64 ) Copyright© 1998, Triola, Elementary Statistics by Addison Wesley Longman 15

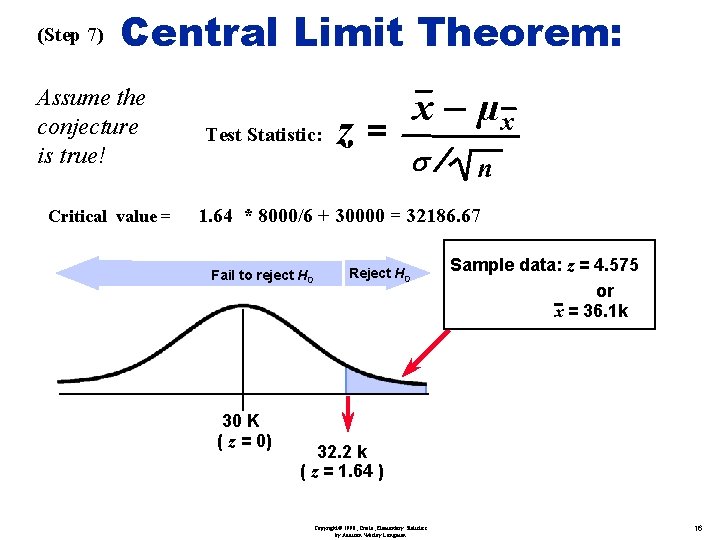
(Step 7) Central Limit Theorem: Assume the conjecture is true! Critical value = Test Statistic: z= x – µx s/ n 1. 64 * 8000/6 + 30000 = 32186. 67 Fail to reject H 0 30 K ( z = 0) Reject H 0 Sample data: z = 4. 575 or x = 36. 1 k 32. 2 k ( z = 1. 64 ) Copyright© 1998, Triola, Elementary Statistics by Addison Wesley Longman 16

Example Step 8: Conclusion: Based on the sample set, there is sufficient evidence to warrant rejection of the claim that “the average starting salary for a computer science gradate is $30, 000 per year”. Copyright© 1998, Triola, Elementary Statistics by Addison Wesley Longman 17

P-Value Method of Testing Hypotheses • Definition v. P-Value (or probability value) the probability of getting a value of the sample test statistic that is at least as extreme as the one found from the sample data, assuming that the null hypothesis is true • Measures how confident we are in rejecting the null hypothesis Copyright© 1998, Triola, Elementary Statistics by Addison Wesley Longman 18

Procedure is the same except for steps 6 and 7 Step 6: Find the P-value Step 7: Report the P-value v. Reject the null hypothesis if the P-value is less than or equal to the significance level a v. Fail to reject the null hypothesis if the Pvalue is greater than the significance level a Copyright© 1998, Triola, Elementary Statistics by Addison Wesley Longman 19

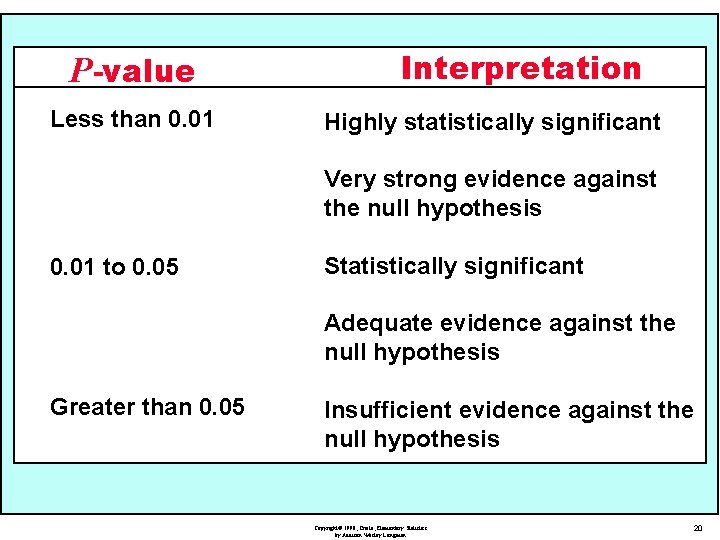
P-value Less than 0. 01 Interpretation Highly statistically significant Very strong evidence against the null hypothesis 0. 01 to 0. 05 Statistically significant Adequate evidence against the null hypothesis Greater than 0. 05 Insufficient evidence against the null hypothesis Copyright© 1998, Triola, Elementary Statistics by Addison Wesley Longman 20

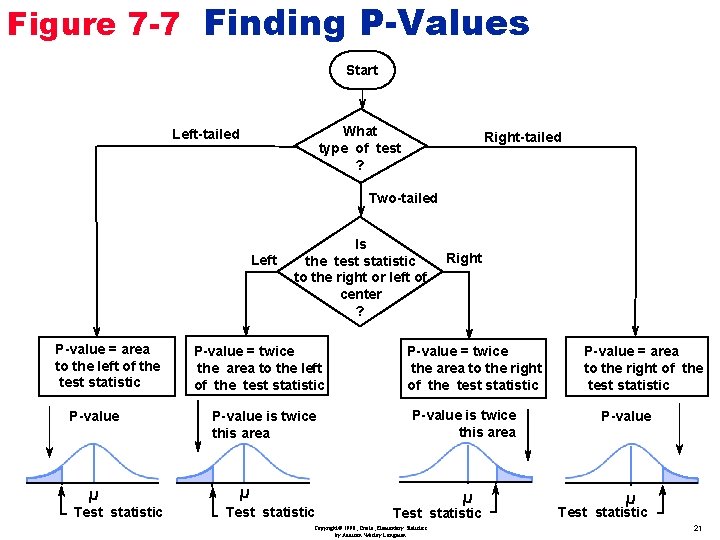
Figure 7 -7 Finding P-Values Start What type of test ? Left-tailed Right-tailed Two-tailed Left P-value = area to the left of the test statistic P-value µ Test statistic Is the test statistic to the right or left of center ? P-value = twice the area to the left of the test statistic P-value is twice this area P-value = twice the area to the right of the test statistic P-value is twice this area µ Test statistic Right µ Test statistic Copyright© 1998, Triola, Elementary Statistics by Addison Wesley Longman P-value = area to the right of the test statistic P-value µ Test statistic 21

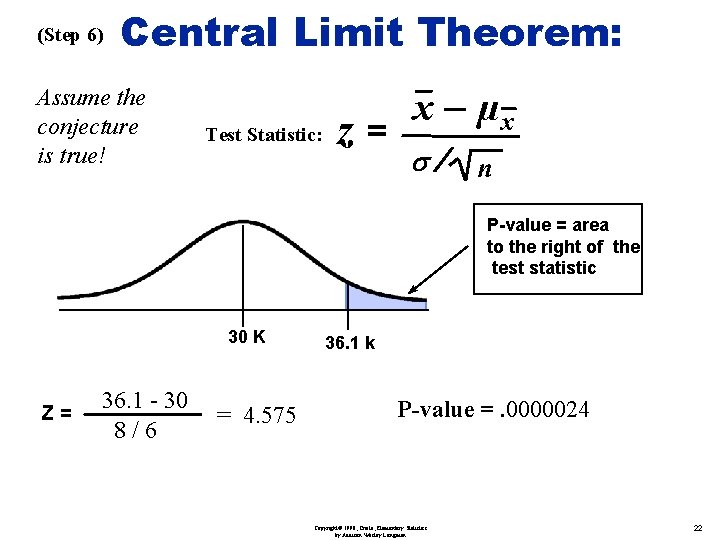
(Step 6) Central Limit Theorem: Assume the conjecture is true! Test Statistic: z= x – µx s/ n P-value = area to the right of the test statistic 30 K Z= 36. 1 - 30 8/6 = 4. 575 36. 1 k P-value =. 0000024 Copyright© 1998, Triola, Elementary Statistics by Addison Wesley Longman 22

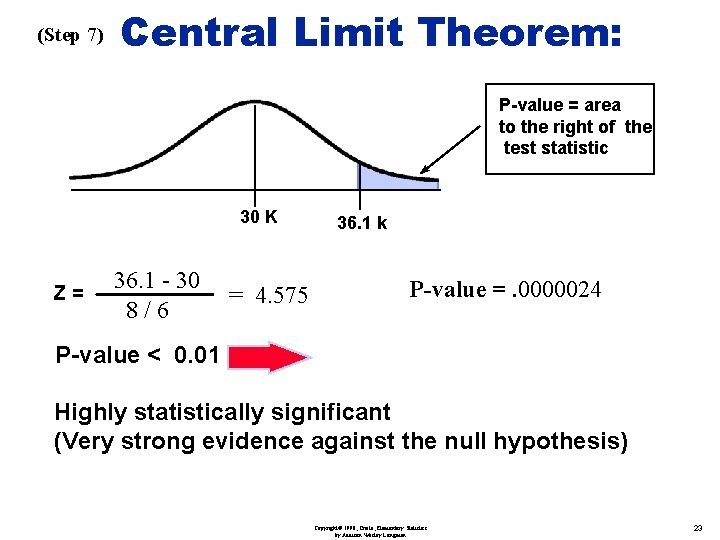
(Step 7) Central Limit Theorem: P-value = area to the right of the test statistic 30 K Z= 36. 1 - 30 8/6 = 4. 575 36. 1 k P-value =. 0000024 P-value < 0. 01 Highly statistically significant (Very strong evidence against the null hypothesis) Copyright© 1998, Triola, Elementary Statistics by Addison Wesley Longman 23