TEST REVIEW Engineering Practicum Test 1 is Next

TEST REVIEW Engineering Practicum Test #1 is Next Week!!! Monday, Tuesday

Science vs. Engineering Science: 1. Systematically obtaining knowledge by observation and experience 2. Use the Scientific Method 3. Empirical / Objective Engineering: 1. Application of math and science by which matter and energy are made useful to people 2. Designing and implementing solutions that fulfill an objective, need, or desire – based on knowledge 3. Subjective solutions based on objective knowledge

Fields of Engineering Major Fields: 1. Aerospace 2. Bioengineering 3. Biomedical 4. Chemical 5. Civil / Structural 6. Electrical 7. Electronic 8. Industrial 9. Material 10. Mechanical 11. Nuclear Source: http: //en. wikipedia. org/wiki/Fields_of_engineering

LETTERING • • Engineer’s communication tool All capital letters BETWEEN GUIDELINES Legible and Consistent LEGIBLE AND CONSISTENT LEGIBLE AND INCONSISTENT

The Facts • A growing number of nations seek to gain global market share in technology-based economic activities. • What’s made global competitiveness possible in the first place? – The Flatteners (4 of 10): 2) 8/9/95 1) 11/9/89 3) Outsourcing and Y 2 K 4) Offshoring • While the national policy response must be multifaceted, ensuring an adequate supply of talented scientists and engineers is one key step.

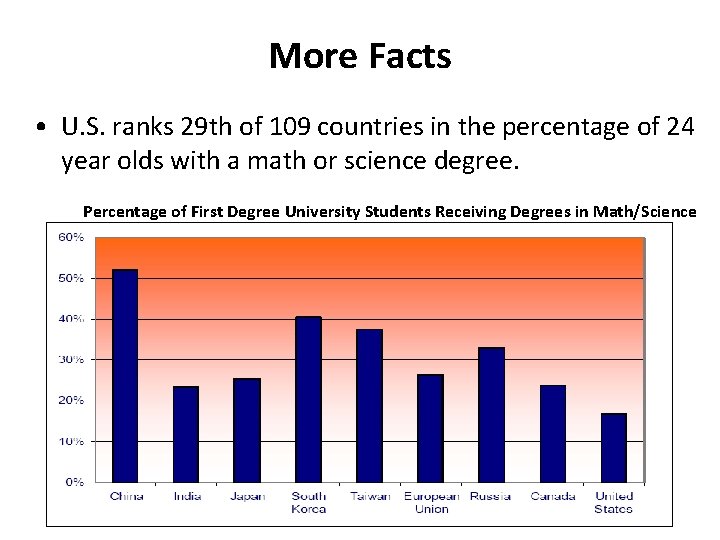
More Facts • U. S. ranks 29 th of 109 countries in the percentage of 24 year olds with a math or science degree. Percentage of First Degree University Students Receiving Degrees in Math/Science

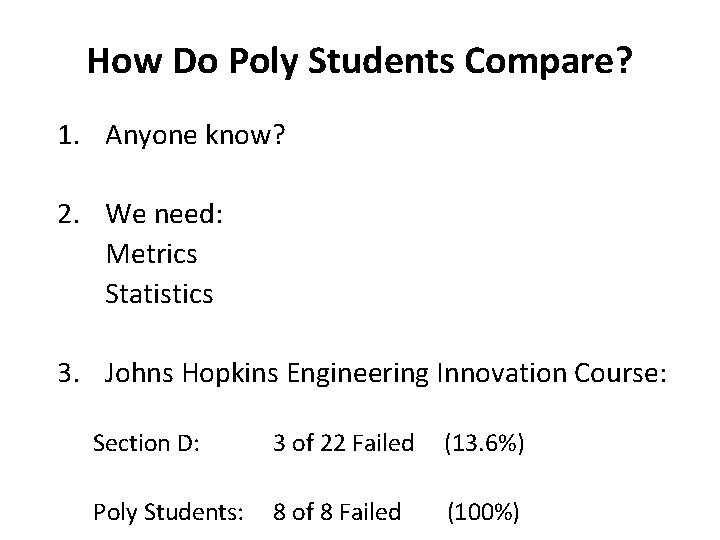
How Do Poly Students Compare? 1. Anyone know? 2. We need: Metrics Statistics 3. Johns Hopkins Engineering Innovation Course: Section D: 3 of 22 Failed (13. 6%) Poly Students: 8 of 8 Failed (100%)

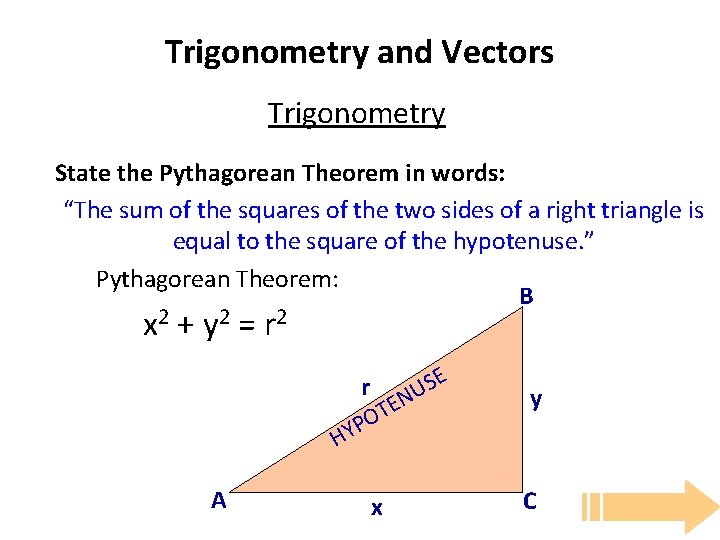
Trigonometry and Vectors Trigonometry State the Pythagorean Theorem in words: “The sum of the squares of the two sides of a right triangle is equal to the square of the hypotenuse. ” Pythagorean Theorem: B x 2 + y 2 = r 2 HY A E S U N r E OT P x y C

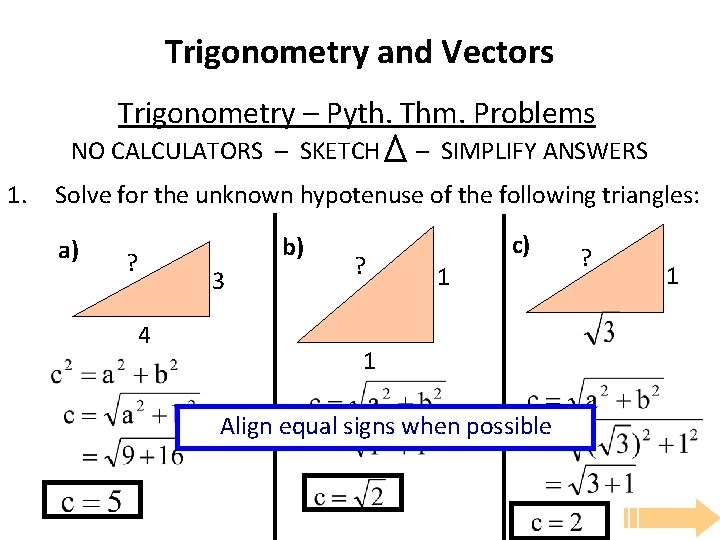
Trigonometry and Vectors Trigonometry – Pyth. Thm. Problems NO CALCULATORS – SKETCH 1. – SIMPLIFY ANSWERS Solve for the unknown hypotenuse of the following triangles: a) b) ? 3 4 ? c) 1 1 Align equal signs when possible ? 1

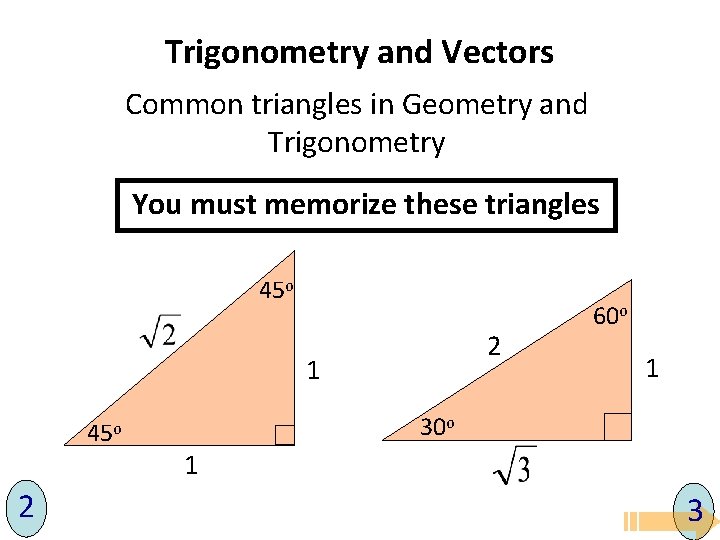
Trigonometry and Vectors Common triangles in Geometry and Trigonometry You must memorize these triangles 45 o 2 1 45 o 2 60 o 1 3

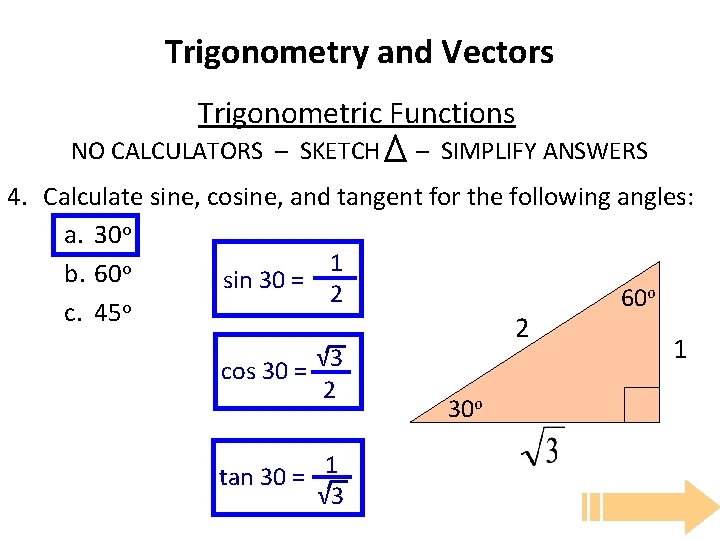
Trigonometry and Vectors Trigonometric Functions NO CALCULATORS – SKETCH – SIMPLIFY ANSWERS 4. Calculate sine, cosine, and tangent for the following angles: a. 30 o 1 b. 60 o sin 30 = o 2 60 c. 45 o cos 30 = √ 3 2 tan 30 = 1 √ 3 2 30 o 1

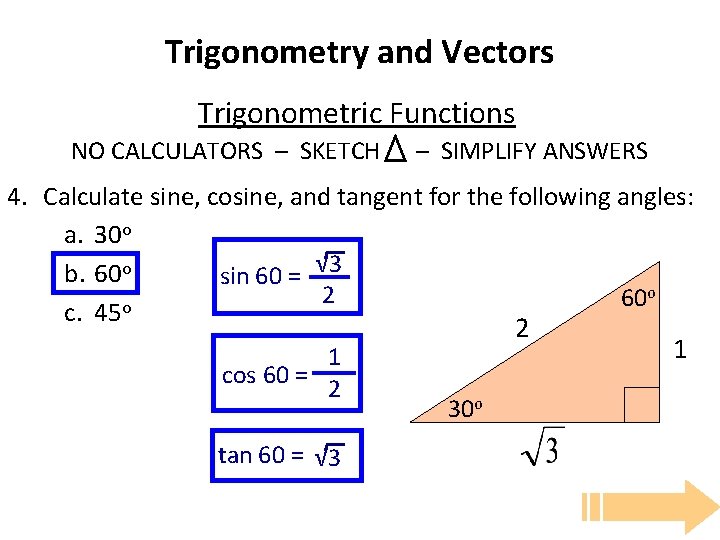
Trigonometry and Vectors Trigonometric Functions NO CALCULATORS – SKETCH – SIMPLIFY ANSWERS 4. Calculate sine, cosine, and tangent for the following angles: a. 30 o √ 3 b. 60 o sin 60 = o 2 60 c. 45 o 1 cos 60 = 2 tan 60 = √ 3 2 30 o 1

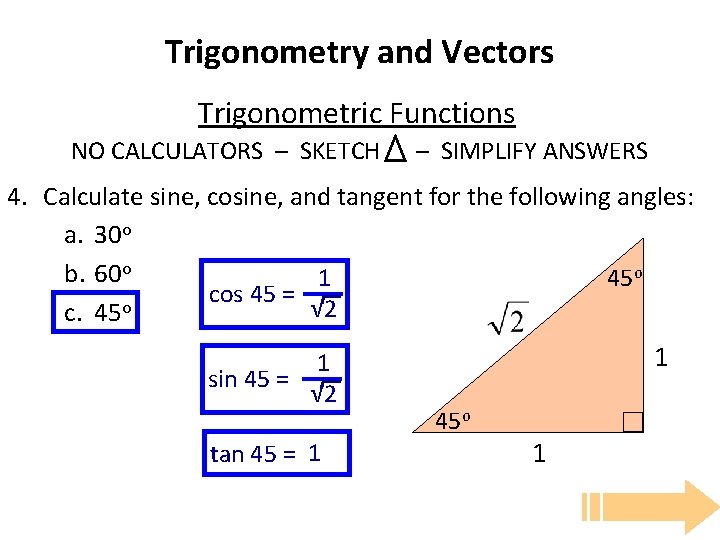
Trigonometry and Vectors Trigonometric Functions NO CALCULATORS – SKETCH – SIMPLIFY ANSWERS 4. Calculate sine, cosine, and tangent for the following angles: a. 30 o b. 60 o 45 o 1 cos 45 = o √ 2 c. 45 1 sin 45 = √ 2 tan 45 = 1 1 45 o 1

Word Problems Read the entire problem through. Note that not all information given is relevant. 1. Write Given, Assign Variables, Sketch and Label Diagram 1. Whenever you write a variable, you must write what that variable means. 2. What are the quantities? Assign variable(s) to quantities. 3. If possible, write all quantities in terms of the same variable. 2. Write Formulas / Equations 1. What are the relationships between quantities? 3. Substitute and Solve 1. Communication: All of your work should communicate your thought process (logic/reasoning). 4. Check Answer, then Box Answer

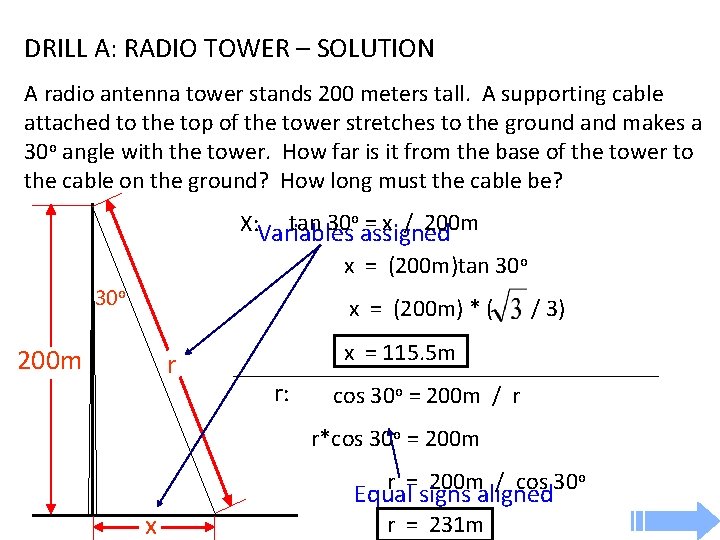
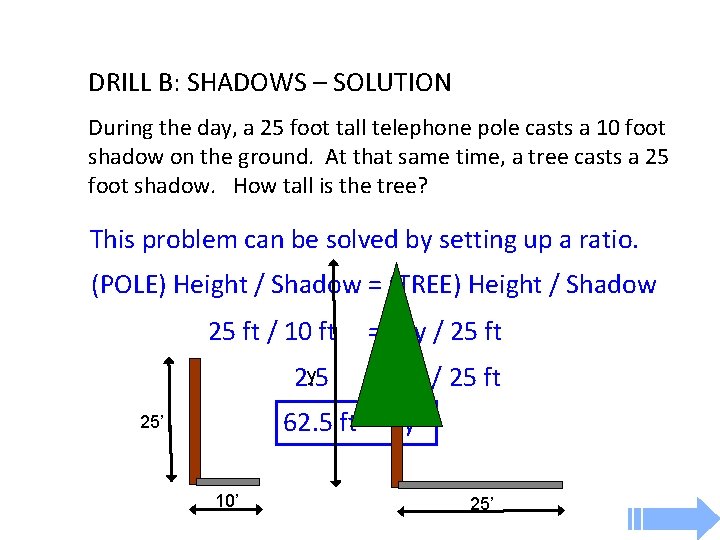
DRILL A: A radio antenna tower stands 200 meters tall. A supporting cable attached to the top of the tower stretches to the ground and makes a 30 o angle with the tower. How far is it from the base of the tower to the cable on the ground? How long must the cable be? DRILL B: During the day, a 25 foot tall telephone pole casts a 10 foot shadow on the ground. At that same time and not far away, a tree casts a 25 foot shadow. How tall is the tree? Engineering Problem Solving 1. Write Given, Assign Variables, Sketch and Label Diagram 2. Write Formulas / Equations 3. Substitute and Solve 4. Check Answer, THEN box answer

DRILL A: RADIO TOWER – SOLUTION A radio antenna tower stands 200 meters tall. A supporting cable attached to the top of the tower stretches to the ground and makes a 30 o angle with the tower. How far is it from the base of the tower to the cable on the ground? How long must the cable be? tan 30 oassigned = x / 200 m X: Variables x = (200 m)tan 30 o x = (200 m) * ( 200 m r / 3) x = 115. 5 m r: cos 30 o = 200 m / r r*cos 30 o = 200 m r = 200 m / cos 30 o x Equal signs aligned r = 231 m

DRILL B: SHADOWS – SOLUTION During the day, a 25 foot tall telephone pole casts a 10 foot shadow on the ground. At that same time, a tree casts a 25 foot shadow. How tall is the tree? This problem can be solved by setting up a ratio. (POLE) Height / Shadow = (TREE) Height / Shadow 25 ft / 10 ft y 2. 5 = y / 25 ft 62. 5 ft = y 25’ 10’ 25’

Systems of Equations • Because two equations impose two conditions on the variables at the same time, they are called a system of simultaneous equations. • When you are solving a system of equations, you are looking for the values that are solutions for all of the system’s equations. • Methods of Solving: 1. Graphing 2. Algebra: 1. Substitution 2. Elimination 1. Addition-or-Subtraction 2. Multiplication in the Addition-or-Subtraction Method

Systems of Equations – Word Problems Classwork: Algebra A: The perimeter of a rectangle is 54 centimeters. Two times the altitude is 3 centimeters more than the base. What is the area of the rectangle? Algebra B: At one point along a trail the angle of elevation from a hiker to the top of a nearby tree is 30 degrees. After walking 40 feet closer to the tree, the angle of elevation from the hiker to the top of the tree is now 60 degrees. Find the height of the tree.

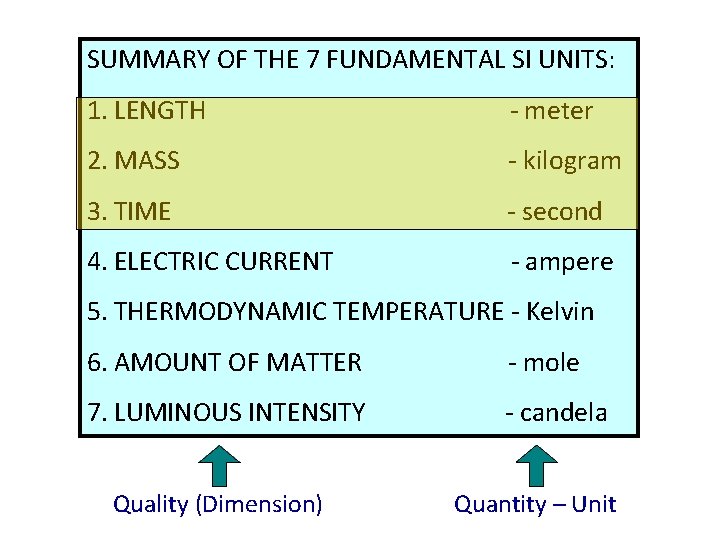
SUMMARY OF THE 7 FUNDAMENTAL SI UNITS: 1. LENGTH - meter 2. MASS - kilogram 3. TIME - second 4. ELECTRIC CURRENT - ampere 5. THERMODYNAMIC TEMPERATURE - Kelvin 6. AMOUNT OF MATTER - mole 7. LUMINOUS INTENSITY - candela Quality (Dimension) Quantity – Unit

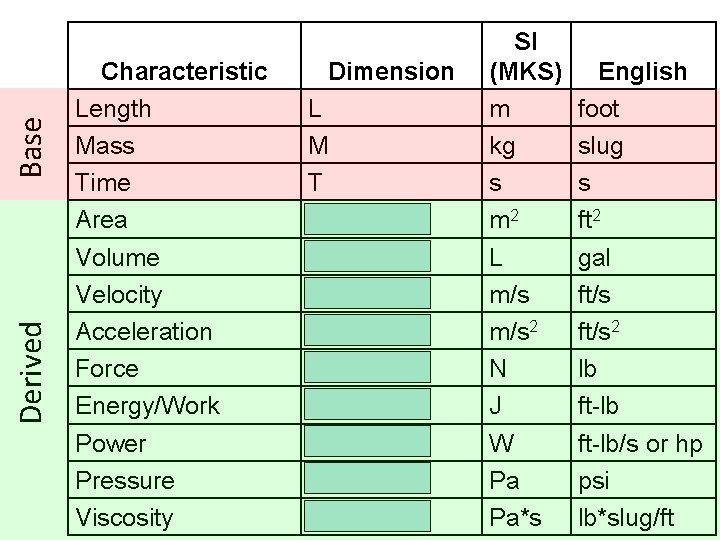
Base Derived Characteristic Length Mass Time Area Volume Velocity Acceleration Force Energy/Work Power Pressure Viscosity Dimension L M T L 2 L 3 LT-1 LT-2 ML 2 T-2 ML 2 T-3 ML-1 T-2 ML-1 T-1 SI (MKS) m kg s m 2 L m/s 2 N J W Pa Pa*s English foot slug s ft 2 gal ft/s 2 lb ft-lb/s or hp psi lb*slug/ft

Dimensional Analysis Fundamental Rules: 2. All terms in an equation must reduce to identical primitive (base) dimensions. Homogeneous Equation Dimensional Homogeneity

Dimensional Analysis Uses: 2. Deduce expressions for physical phenomena. Example: What is the period of oscillation for a pendulum? (time to complete full cycle) We predict that the period T will be a function of m, L, and g: