Test for Parallelograms LESSON 6 3 Coordinate Proof

Test for Parallelograms LESSON 6 -3

Coordinate Proof A proof that uses figures in the coordinate plane and algebra to prove geometric concepts. Don’t forget the Theorems from Lesson 6 -2

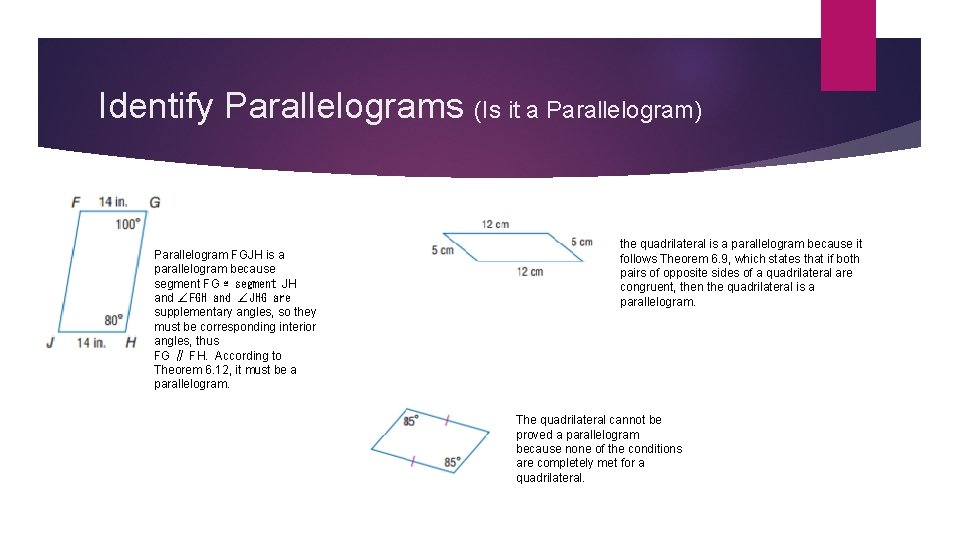
Identify Parallelograms (Is it a Parallelogram) Parallelogram FGJH is a parallelogram because segment FG ≅ segment JH and ∠FGH and ∠JHG are supplementary angles, so they must be corresponding interior angles, thus FG ∥ FH. According to Theorem 6. 12, it must be a parallelogram. the quadrilateral is a parallelogram because it follows Theorem 6. 9, which states that if both pairs of opposite sides of a quadrilateral are congruent, then the quadrilateral is a parallelogram. The quadrilateral cannot be proved a parallelogram because none of the conditions are completely met for a quadrilateral.

Example: Theorem 6. 11 says that diagonals bisect each other and create two congruent versions of each line. So FK = KH and JK = KG and the problem tells us that it will be a parallelogram. FK = KH 3 x-1 = 2 x+3 +1 JK and = KG 6 y-2 = 4 y+3 +1 +2 +2 3 x = 2 x+4 6 y = 4 y+ 5 -2 x -4 y x= 4 2 y =5 2 y=5/2 2

Example:

Example: Now prove it is a parallelogram by the distance formula. If we can prove that the opposite sides are congruent, we can prove this is a parallelogram. Distance Formula: So we know segment KL and segment NM are congruent. So we know that these two sides are congruent also. According to Theorem 6. 9, if both pairs of opposite sides of a quadrilateral are congruent, than the quadrilateral is congruent.

Example: Now prove that the diagonals bisect each other. We can prove a parallelogram if the diagonals bisect each other, which means that they should meet at exact the same point. So we will use the midpoint theorem to see if the midpoints are the same. So we need to find the midpoint of KM and LN. So according to Theorem 6. 11, If the diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram.