Tessellations What is a tessellation If many copies

Tessellations

What is a tessellation? If many copies of a shape can be used to cover a surface, without leaving any gaps between them, then we say that the shape will tessellate. The pattern that is formed is called a tessellation. Simply put: A tessellation is like a puzzle that repeats a particular pattern. For example:

In nature and life, they appear often: Honeycombs. . . Mud flats. . . In games, like checkers. .

Tessellations in Nature snake skin armadillo armor spider web

Tessellations are all around us: Look for tessellations in walls, patios and pavements.

Tessellations are all around us: Common shapes can be arranged in unusual ways Sometimes an unusual shape will tessellate

Tessellations are all around us: Sometimes 2 or more different shapes will tessellate.

Tessellations Around the House • Tessellations can be found in quilts, floor tiling, and wallpaper.

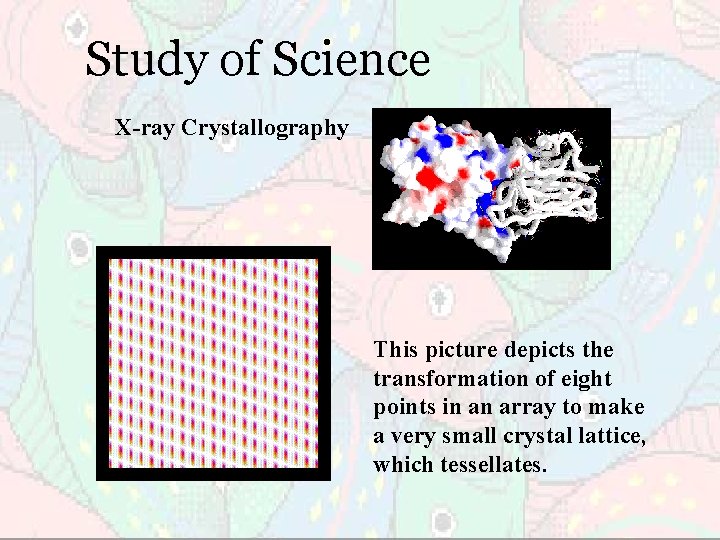
Study of Science X-ray Crystallography This picture depicts the transformation of eight points in an array to make a very small crystal lattice, which tessellates.

more science…. This image suggests the relationship between tessellations, symmetry, and x-ray crystallograpy.

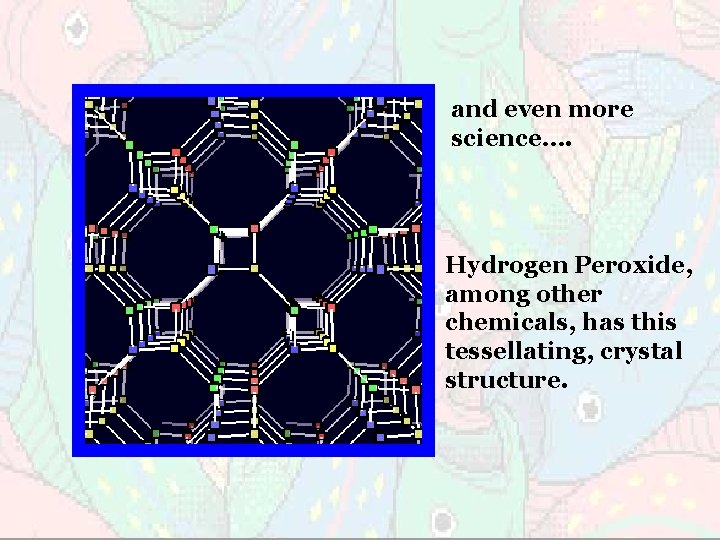
and even more science…. Hydrogen Peroxide, among other chemicals, has this tessellating, crystal structure.

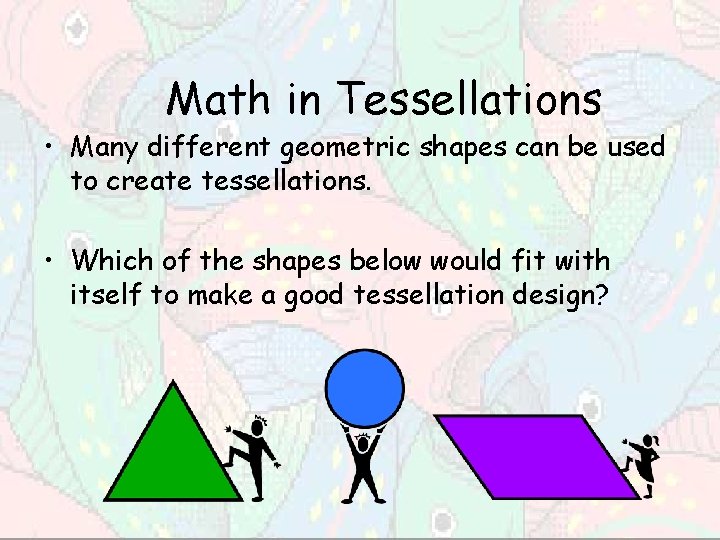
Math in Tessellations • Many different geometric shapes can be used to create tessellations. • Which of the shapes below would fit with itself to make a good tessellation design?

The mathematics of the Regular Tessellation. . . • A regular polygon tessellation is constructed from regular polygons. • Regular polygons have equal sides and equal angles. • The regular polygons must fill the plane at each vertex, with repeating patterns and no overlapping pieces. Note: this pentagon does not fit into the vertex… therefore it is not a regular tessellation.

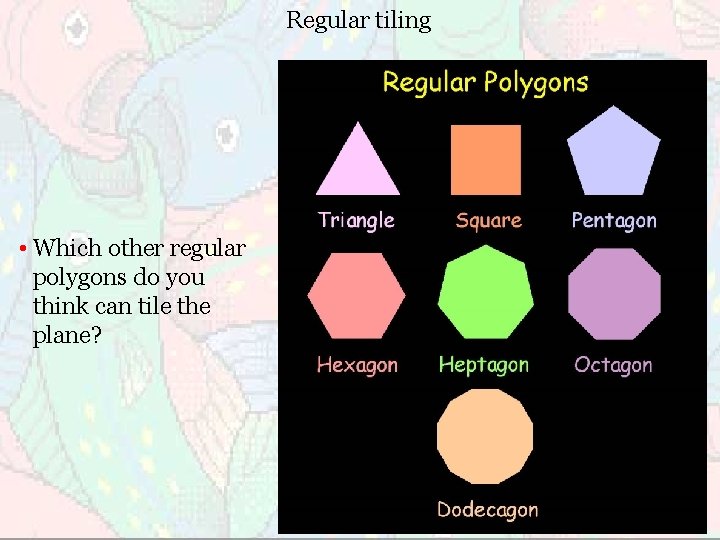
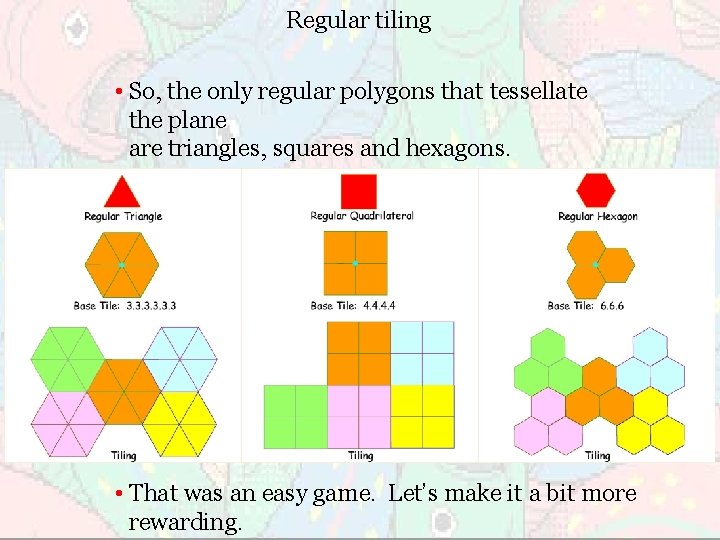
Regular tiling • Which other regular polygons do you think can tile the plane?

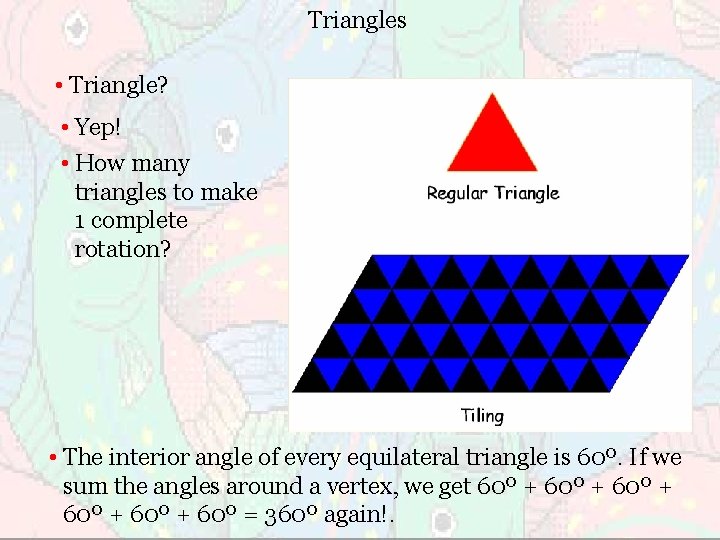
Triangles • Triangle? • Yep! • How many triangles to make 1 complete rotation? • The interior angle of every equilateral triangle is 60º. If we sum the angles around a vertex, we get 60º + 60º + 60º = 360º again!.

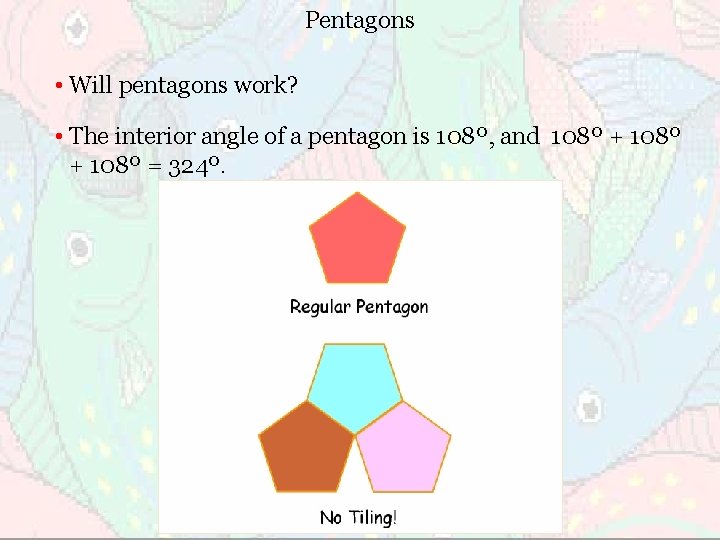
Pentagons • Will pentagons work? • The interior angle of a pentagon is 108º, and 108º + 108º = 324º.

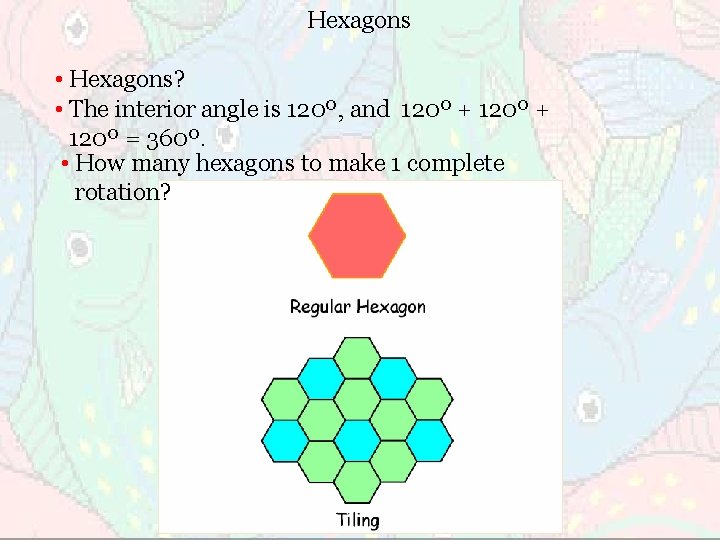
Hexagons • Hexagons? • The interior angle is 120º, and 120º + 120º = 360º. • How many hexagons to make 1 complete rotation?

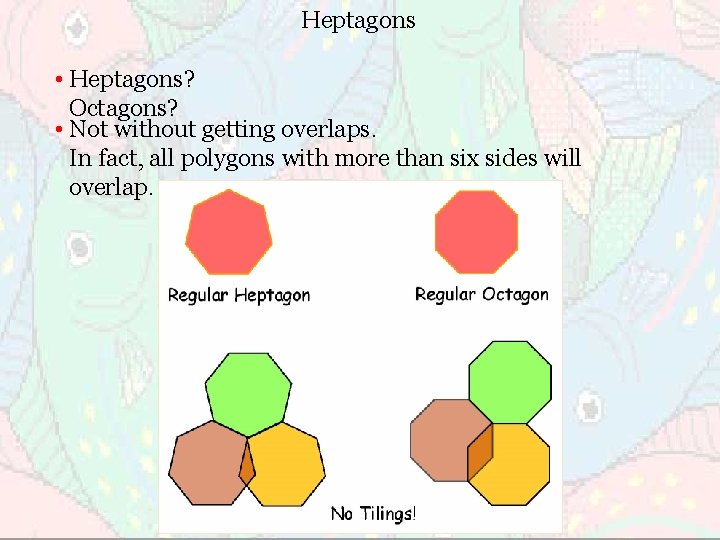
Heptagons • Heptagons? Octagons? • Not without getting overlaps. In fact, all polygons with more than six sides will overlap.

Regular tiling • So, the only regular polygons that tessellate the plane are triangles, squares and hexagons. • That was an easy game. Let’s make it a bit more rewarding.

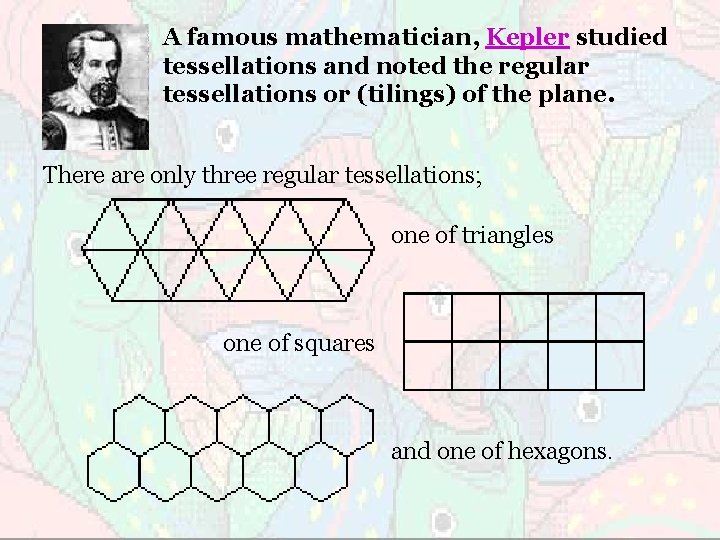
A famous mathematician, Kepler studied tessellations and noted the regular tessellations or (tilings) of the plane. There are only three regular tessellations; one of triangles one of squares and one of hexagons.

This is NOT a regular polygon tessellation, because. . . vertex space The plane is not filled at the vertex, because there is space left over. A regular polygon tessellation, can be changed using “alterations” to the sides of the polygon. These alterations are called transformations.

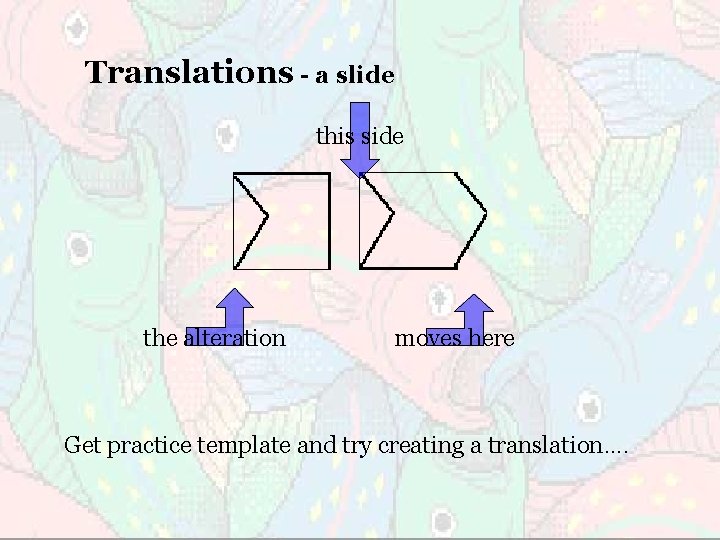
Three Common Transformations 1. Translation, which is a slide of one side of the polygon. 2. Reflection, which is a flip or mirror image of one side of the polygon. 3. Rotation, which is a turn of a side around one vertex of the polygon.

Translations - a slide this side the alteration moves here Get practice template and try creating a translation….

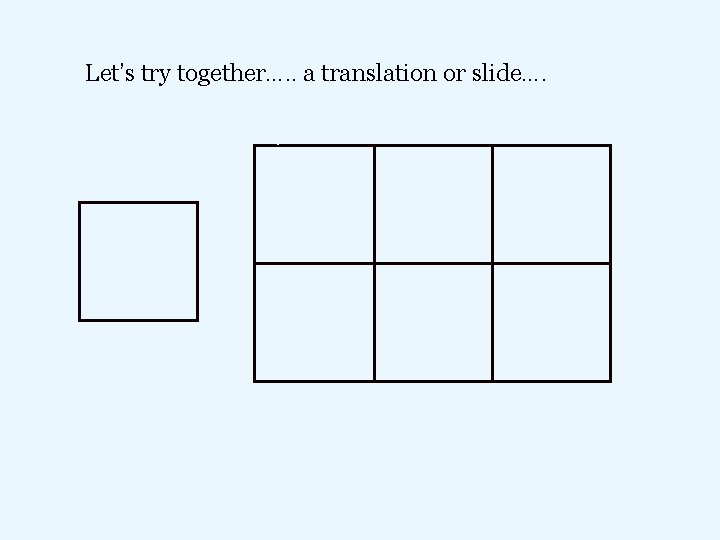
Let’s try together…. . a translation or slide….

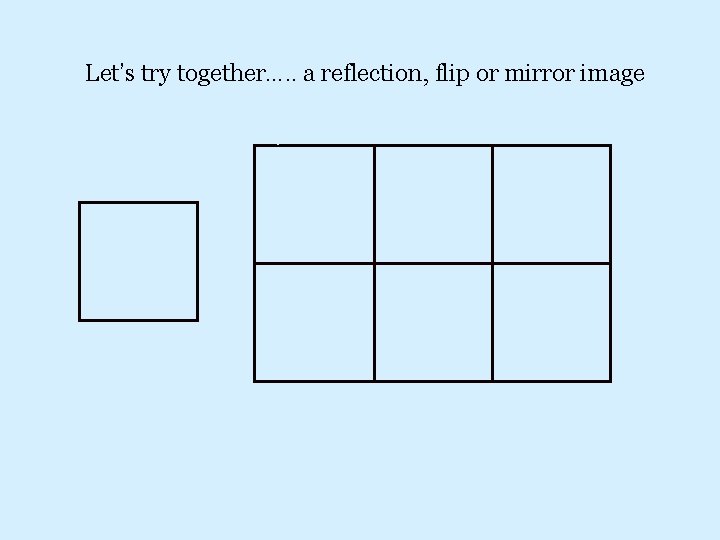
Reflections - mirror images the alteration flips here Get practice template and try creating a reflection….

Let’s try together…. . a reflection, flip or mirror image

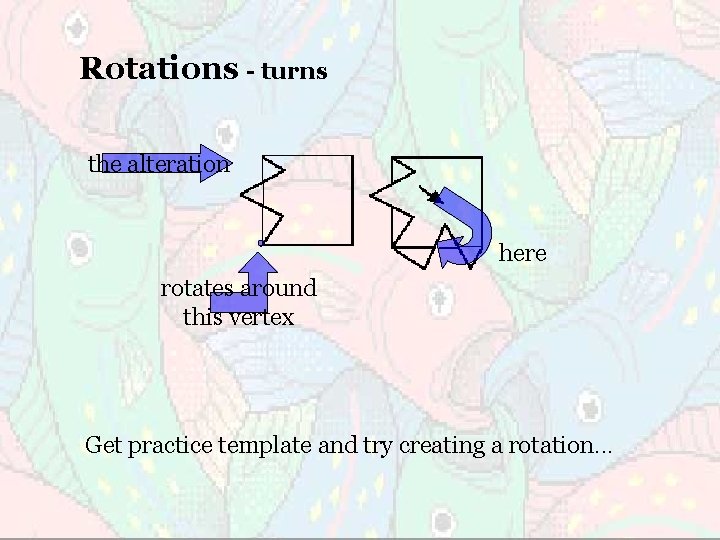
Rotations - turns the alteration here rotates around this vertex Get practice template and try creating a rotation. . .

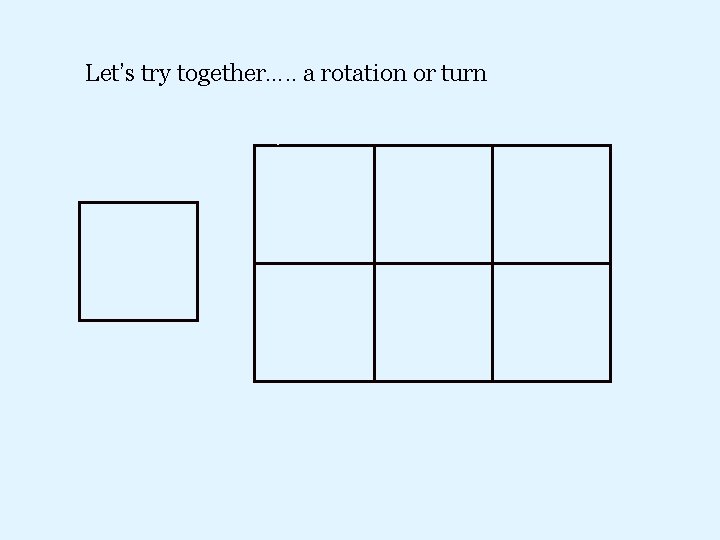
Let’s try together…. . a rotation or turn

Tessellations by M. C. Escher

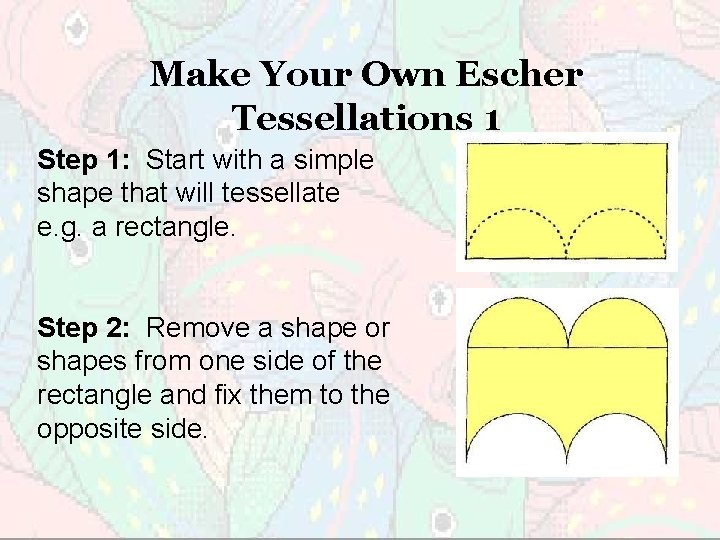
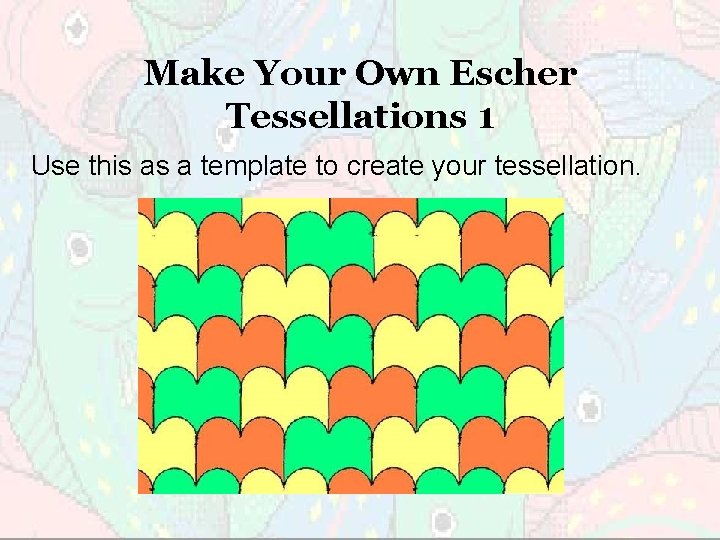
Make Your Own Escher Tessellations 1 Step 1: Start with a simple shape that will tessellate e. g. a rectangle. Step 2: Remove a shape or shapes from one side of the rectangle and fix them to the opposite side.

Make Your Own Escher Tessellations 1 Use this as a template to create your tessellation.

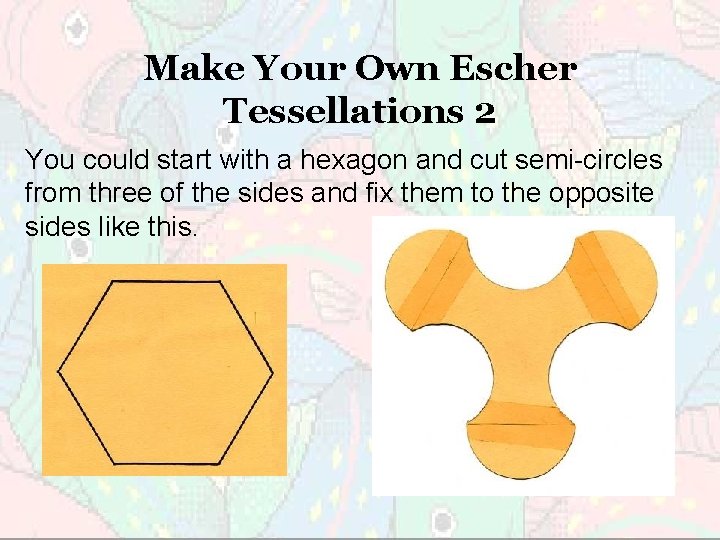
Make Your Own Escher Tessellations 2 You could start with a hexagon and cut semi-circles from three of the sides and fix them to the opposite sides like this.

Make Your Own Escher Tessellations 2

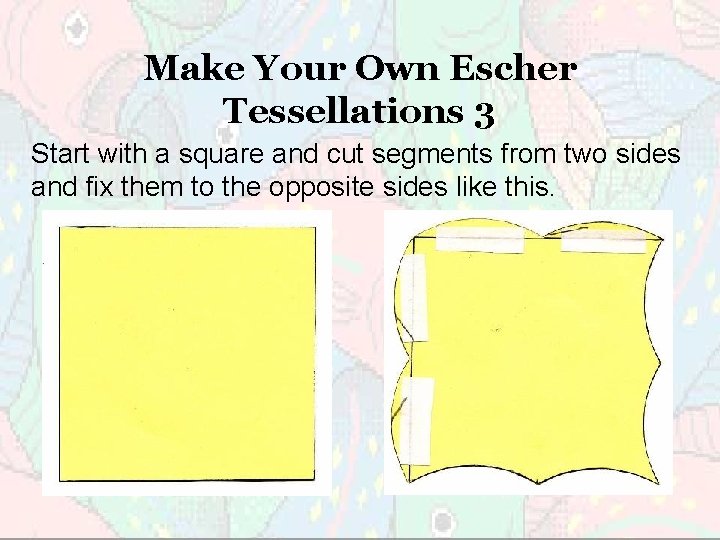
Make Your Own Escher Tessellations 3 Start with a square and cut segments from two sides and fix them to the opposite sides like this.

Make Your Own Escher Tessellations 3

Professional Tessellation Designs Sun and Moon Fish M. C. Escher Robert Ingalls • Many artists have created master works of art using the simple rules of tessellations. • M. C. Escher and Robert Ingalls are among many tessellation artists. • Can you spot the repeating shape?

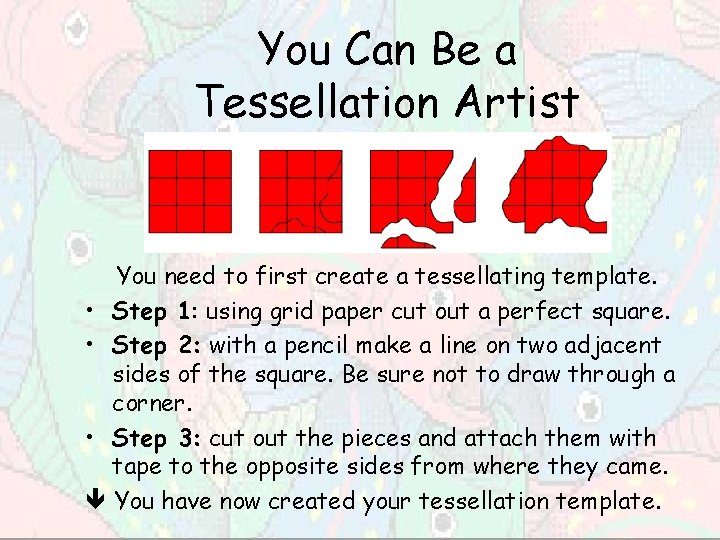
You Can Be a Tessellation Artist You need to first create a tessellating template. • Step 1: using grid paper cut out a perfect square. • Step 2: with a pencil make a line on two adjacent sides of the square. Be sure not to draw through a corner. • Step 3: cut out the pieces and attach them with tape to the opposite sides from where they came. You have now created your tessellation template.

Seeing a Figure • Looking at your tessellation template, study the sides and the shape to decide what sort of figure you might see. • The person who designed this form saw an elephant and an elf. • Are there any other different forms that you might see? • When looking for the shape be sure not to see too much detail as it can make the art work too crowded.

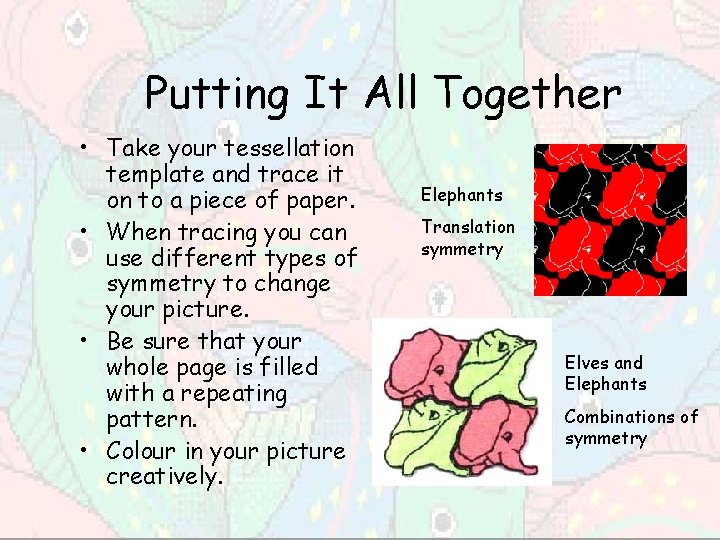
Putting It All Together • Take your tessellation template and trace it on to a piece of paper. • When tracing you can use different types of symmetry to change your picture. • Be sure that your whole page is filled with a repeating pattern. • Colour in your picture creatively. Elephants Translation symmetry Elves and Elephants Combinations of symmetry

Extras . . . Is this a regular tessellation? What kind of tessellation is this? Tessellation internet activity Cool site for interactive Javascript tessellations. Constructing tessellations - Claris/Appleworks, Hyper. Card, Hyper. Studio, Geometry Sketchpad, Windows Paint and more.

Links • Totally Tessellated - Think. Quest winner - great site, instruction, information. http: //library. advanced. org/16661/ • Tessellations Tutorials - Math Forum site http: //forum. swarthmore. edu/sum 95/suzanne/tess. intro. html - site for construction of tessellations. http: //forum. swarthmore. edu/sum 95/suzanne/links. html - great list of tessellation links • Math. Com - List of good tessellation links http: //test. math. com/students/wonders/tessellations. html • World of Escher site - commerical site with gallery of Dutch artist, Escher who was famous for his tessellation art. http: //World. Of. Escher. com/gallery/ • Science University’s Tilings Around Us Site. http: //www. Science. U. com/geometry/articles/tilings. html • Other links from Forum. http: //forum. swarthmore. edu/library/topics/transform_g/ The end. . .

Paper Folding Movie Click to play the movie.