Tessellation By Ahmed Khalil 2 Outline 1 Tessellation

Tessellation By Ahmed Khalil

2 Outline 1 Tessellation: What & Why ? 2 Tessellation Patterns 3 Tessellation Algorithms 4 Fractional Tessellation 5 Next Step ? Wednesday, January 26, 2022

3 Outline 1 Tessellation: What & Why ? 2 Tessellation Patterns 3 Tessellation Algorithms 4 Fractional Tessellation 5 Next Step ? Wednesday, January 26, 2022

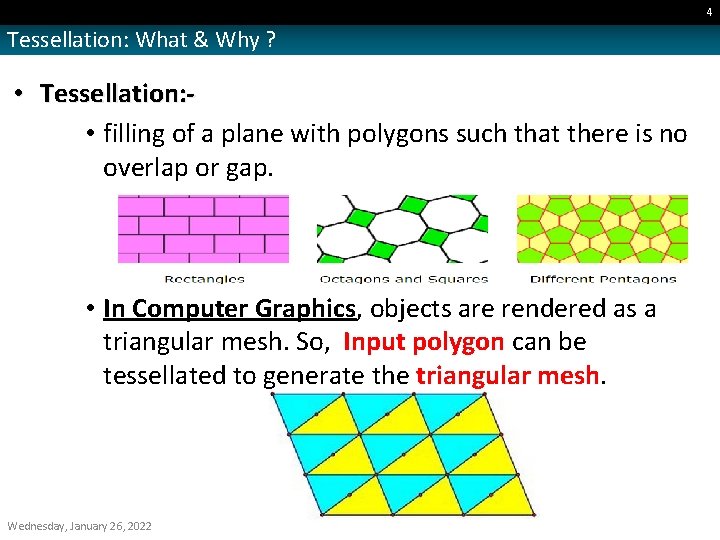
4 Tessellation: What & Why ? • Tessellation: • filling of a plane with polygons such that there is no overlap or gap. • In Computer Graphics, objects are rendered as a triangular mesh. So, Input polygon can be tessellated to generate the triangular mesh. Wednesday, January 26, 2022

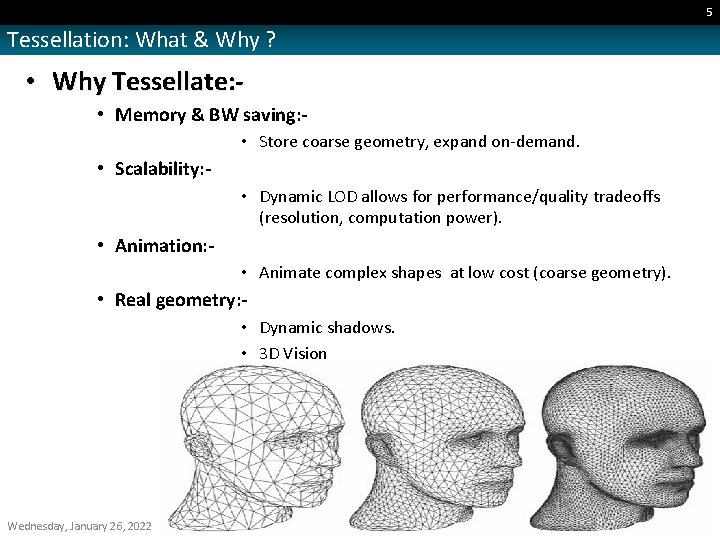
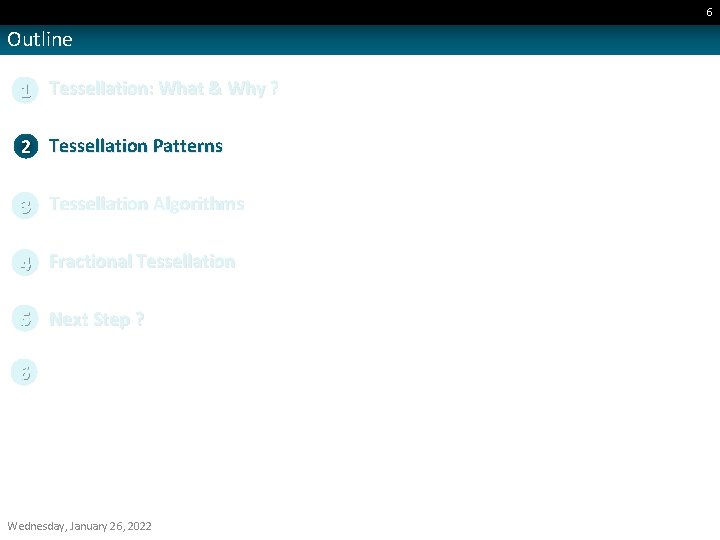
5 Tessellation: What & Why ? • Why Tessellate: • Memory & BW saving: • Store coarse geometry, expand on-demand. • Scalability: • Dynamic LOD allows for performance/quality tradeoffs (resolution, computation power). • Animation: • Animate complex shapes at low cost (coarse geometry). • Real geometry: • Dynamic shadows. • 3 D Vision Wednesday, January 26, 2022

6 Outline 1 Tessellation: What & Why ? 2 Tessellation Patterns 3 Tessellation Algorithms 4 Fractional Tessellation 5 Next Step ? 6 Wednesday, January 26, 2022

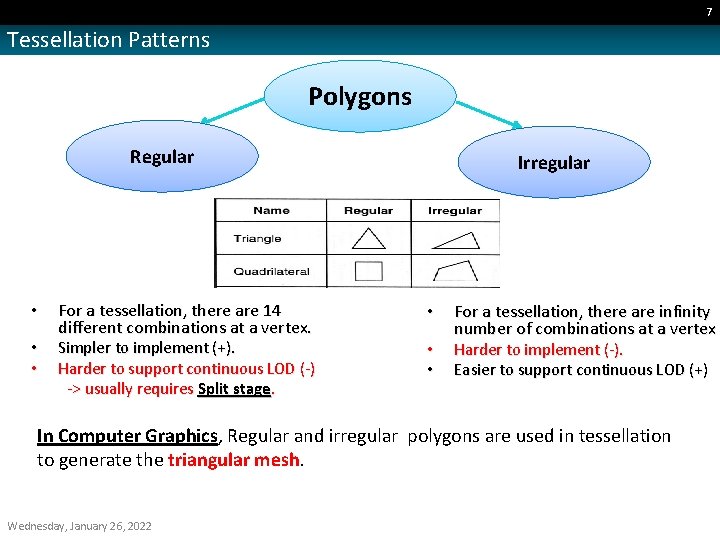
7 Tessellation Patterns Polygons Regular • • • For a tessellation, there are 14 different combinations at a vertex. Simpler to implement (+). Harder to support continuous LOD (-) -> usually requires Split stage. Irregular • • • For a tessellation, there are infinity number of combinations at a vertex Harder to implement (-). Easier to support continuous LOD (+) In Computer Graphics, Regular and irregular polygons are used in tessellation to generate the triangular mesh. Wednesday, January 26, 2022

8 Tessellation Patterns • A) Tessellations with regular Polygons: 1) Regular Tessellation: - Periodic, uniform, and consists of identical regular polygons. - There are only three polygons where interior angles divide evenly into 360 degrees Triangle, Square, and Hexagon. - Uniform: - means the same type of polygon(s) at each vertex Wednesday, January 26, 2022

9 Tessellation Patterns • A) Tessellations with regular Polygons: 2) Semi-regular Tessellation: - Periodic, uniform, and consists of different regular polygons. - There are eight semi-regular tessellation patterns. The most-common Semi-regular Tessellation Wednesday, January 26, 2022

10 Tessellation Patterns • A) Tessellations with regular Polygons: 3) Non-uniform periodic Tessellations: - Have visible patterns but the vertices are different. - Although the restriction still exists to the polygons used in the 14 combinations, there an infinite number of such tessellation. Tessellation pattern shows some vertices with hexagons and two squares and a triangle and some with two squares and 3 triangles. Wednesday, January 26, 2022

11 Tessellation Patterns • A) Tessellations with regular Polygons: 4) Non-uniform Non-periodic Tessellations: - there an infinite number of such tessellations. - it is much harder to construct with no given pattern or period. Again, the vertices are limited to the 14 typical vertices. Wednesday, January 26, 2022

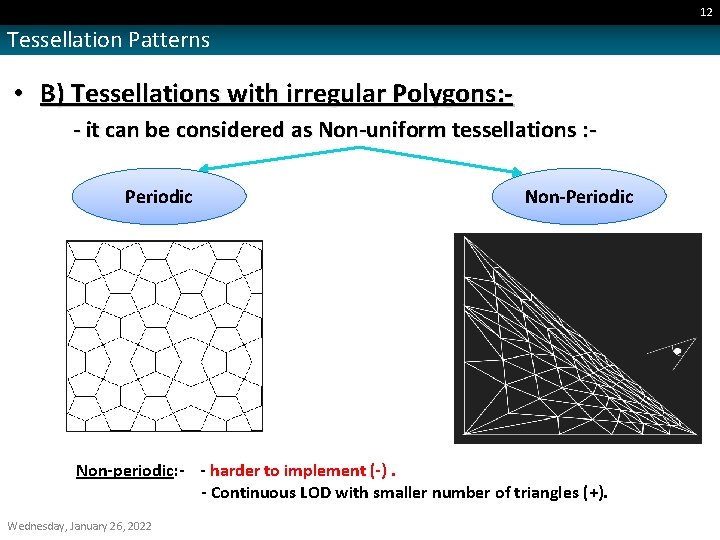
12 Tessellation Patterns • B) Tessellations with irregular Polygons: - it can be considered as Non-uniform tessellations : Periodic Non-periodic: - - harder to implement (-). - Continuous LOD with smaller number of triangles (+). Wednesday, January 26, 2022

13 Outline 1 Tessellation: What & Why ? 2 Tessellation Patterns 3 Tessellation Algorithms 4 Fractional Tessellation 5 Next Step ? Wednesday, January 26, 2022

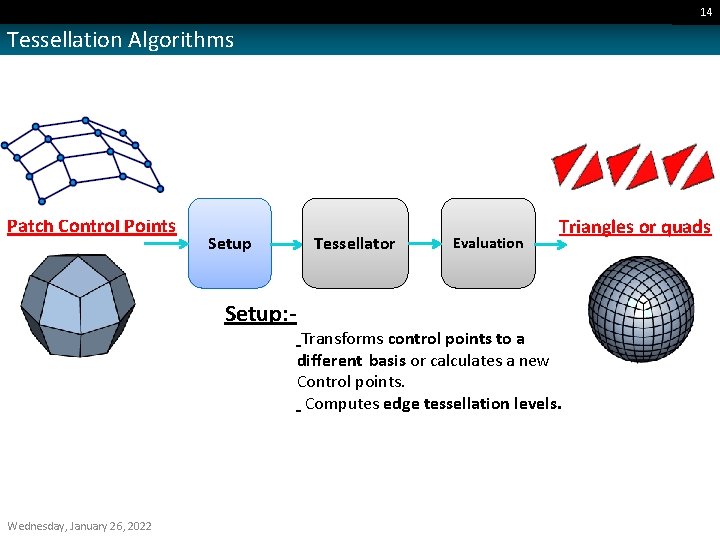
14 Tessellation Algorithms Patch Control Points Setup: - Wednesday, January 26, 2022 Tessellator Evaluation Triangles or quads Transforms control points to a different basis or calculates a new Control points. Computes edge tessellation levels.

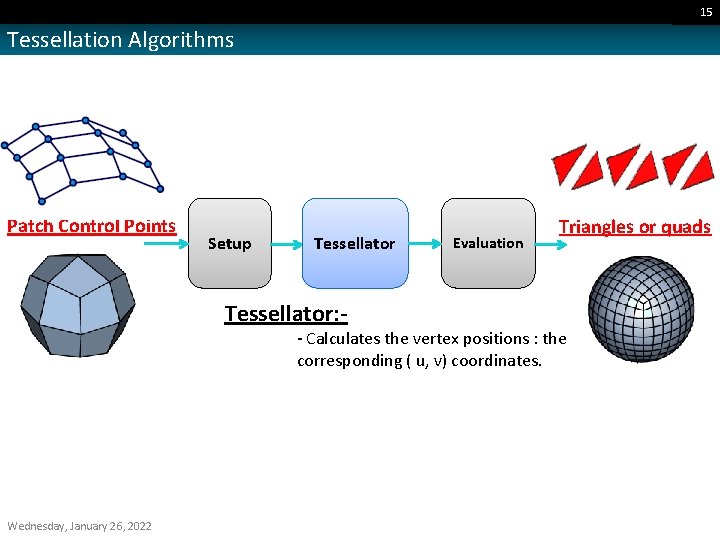
15 Tessellation Algorithms Patch Control Points Setup Tessellator: - Evaluation Triangles or quads - Calculates the vertex positions : the corresponding ( u, v) coordinates. Wednesday, January 26, 2022

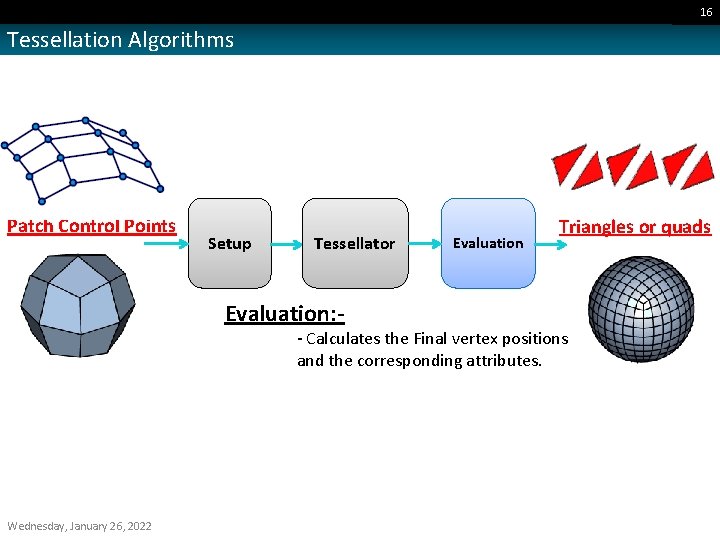
16 Tessellation Algorithms Patch Control Points Setup Tessellator Evaluation: - Evaluation Triangles or quads - Calculates the Final vertex positions and the corresponding attributes. Wednesday, January 26, 2022

17 Tessellation Algorithms • For the vertex points, Tessellation can be divided into two major stages: • Split (Subdivision): - Recursively subdivides the input patch into sub-patches until the sub-patch edges can be diced uniformly. • Dice: - Adaptively tessellates sub-patches generated by Split into polygon meshes. • For the control points, there are different methods to calculate new control point according the input patch type (Bezier surfaces, NURBS surface, . . . etc. ). Wednesday, January 26, 2022 Non-uniform Rational B-spline Surface

18 Tessellation Algorithms • Tessellation Algorithms: • • • Point-Normal (PN) Triangles. Catmull-Clark Subdivision Surfaces. Diag-Split Tessellation. Phong Tessellation. Centroidal Voronoi Tessellation. • Various Tessellation Schemes differ at: • • Wednesday, January 26, 2022 Number of vertices in the patch primitive Control Point Computation. Pass through or higher order parametric patch. Surface Evaluation.

19 Tessellation Algorithms • 1) PN-Triangles : • Simple tessellation scheme provides smoother silhouettes and better shading. • Operates directly on triangle meshes with per vertex Positions and Normals. • No-Split algorithm: - the input patch (Bezier Surface) is tessellated directly. • Implemented in D 3 D 11 Two programmable stage (Hull & Domain Shaders). One fixed function stage (Tessellator). • Proposed by Alex Vlachos, 2003. Modified by Tamy Boubekeur, 2005 and John Mc. Donald 2010. Wednesday, January 26, 2022

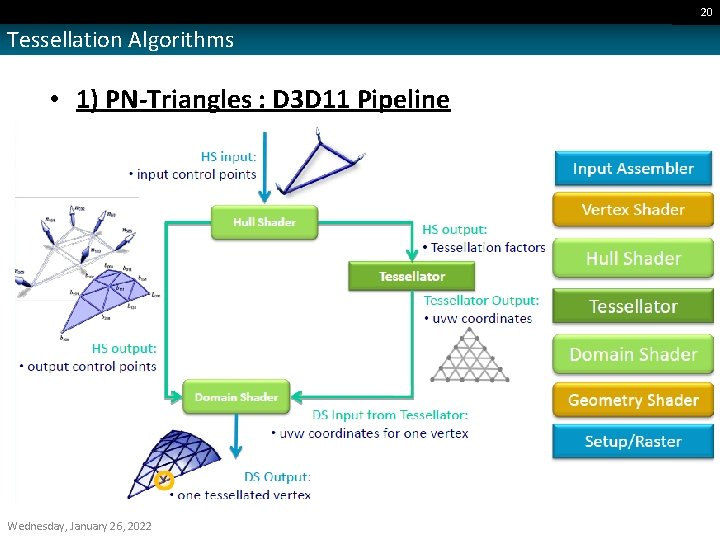
20 Tessellation Algorithms • 1) PN-Triangles : D 3 D 11 Pipeline Wednesday, January 26, 2022

21 Tessellation Algorithms • 1) PN-Triangles : D 3 D 11 Pipeline • Hull Shader: Transforms control points to a different basis and computes edge tessellation levels. Wednesday, January 26, 2022 Computing Position Control Points

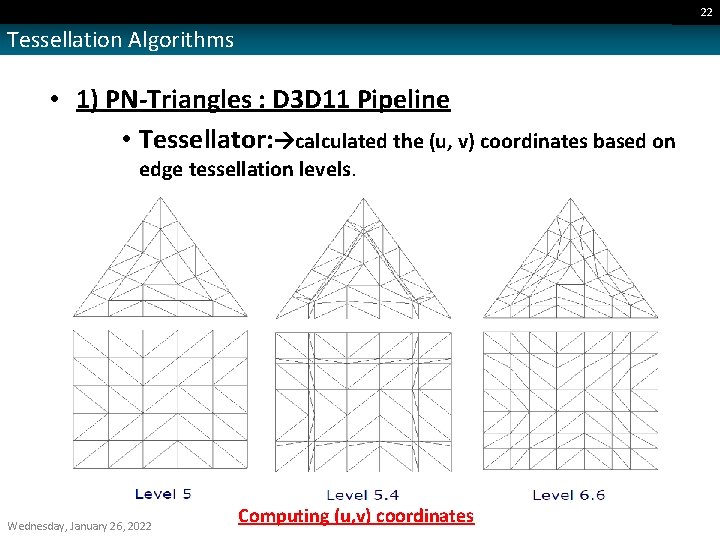
22 Tessellation Algorithms • 1) PN-Triangles : D 3 D 11 Pipeline • Tessellator: calculated the (u, v) coordinates based on edge tessellation levels. Wednesday, January 26, 2022 Computing (u, v) coordinates

23 Tessellation Algorithms • 1) PN-Triangles : D 3 D 11 Pipeline • Domain Shader: Evaluate surface given parametric UV coordinates, interpolate attributes, and apply displacement. Wednesday, January 26, 2022 Evaluation of the surface

24 Tessellation Algorithms • 2) Catmull-Clark Subdivision Surface: • Given a Coarse polygon that approximates the shape of the surface, A subdivision algorithm recursively refines this base mesh to produce a sequence of finer control meshes that converge to a smooth limit. surface. • Have become a standard modeling primitive in computer generated motion pictures and 3 D games. • • The Future tessellation algorithm in real-time applications. Proposed by Ed Catmull and Jim Clark, 1978. Wednesday, January 26, 2022

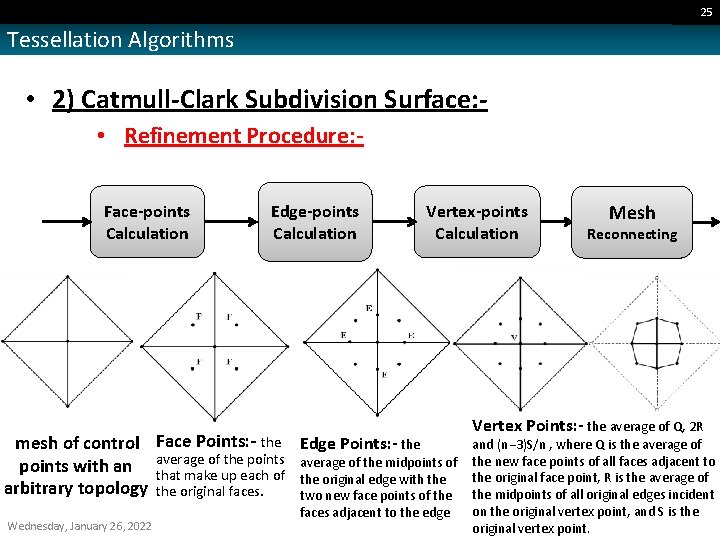
25 Tessellation Algorithms • 2) Catmull-Clark Subdivision Surface: • Refinement Procedure: Face-points Calculation Edge-points Calculation Vertex-points Calculation mesh of control Face Points: - the Edge Points: - the of the points average of the midpoints of points with an average that make up each of the original edge with the arbitrary topology the original faces. two new face points of the Wednesday, January 26, 2022 faces adjacent to the edge Mesh Reconnecting Vertex Points: - the average of Q, 2 R and (n− 3)S/n , where Q is the average of the new face points of all faces adjacent to the original face point, R is the average of the midpoints of all original edges incident on the original vertex point, and S is the original vertex point.

26 Tessellation Algorithms • 2) Catmull-Clark Subdivision Surface: • On-line refinement process: -Adaptive Global Mesh Refinement: Not Flat - Pateny implements subdivision according to Refinement its standard definition. Process - consumes limited removable disk space and GPU memory, and requires significant bus bandwidth. Flatness Test - To overcome these problem, other technique proposed: Direct Evaluation (Stam). Flat - algorithm complexity (-) - Crease Evaluation Challenge(-) Patch approximation (Charles Loop). Flatness: - the distance from the polygonal mesh to the limit surface measured in screen pixels Wednesday, January 26, 2022

27 Tessellation Algorithms • 2) Catmull-Clark Subdivision Surface: • On-line refinement process: - Approximating Catmull-Clark Subdivision Surfaces with Bicubic Patches: Charles Loop proposed an efficient algorithm for approximating Catmull-Clark subdivision surfaces using a minimal set of bicubic patches. For each quadrilateral face of the control mesh, we construct a geometry patch and a pair of tangent patches. The geometry patches approximate the shape of the Catmull-Clark surface. The tangent patches approximate the tangent fields of the Catmull-Clark surface to make the patch surface appear smooth along patch edges containing an extraordinary vertex. Wednesday, January 26, 2022

28 Tessellation Algorithms • 2) Catmull-Clark Subdivision Surface: • On-line refinement process: - Approximating Catmull-Clark Subdivision Surfaces with Bicubic Patches: Each quadrilateral face in a Catmull-Clark control mesh corresponds to a single bicubic patch except for quadrilaterals that contain an extraordinary vertex. Requires 25 control points to perform evaluation. Control point labeling for a Bezier patch. Wednesday, January 26, bicubic 2022 Masks for determining Bezier control points from a uniform bicubic B-spline surface

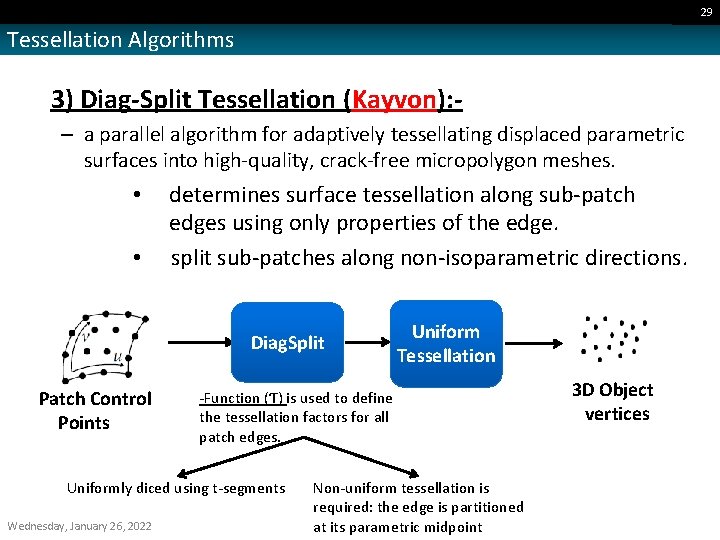
29 Tessellation Algorithms 3) Diag-Split Tessellation (Kayvon): – a parallel algorithm for adaptively tessellating displaced parametric surfaces into high-quality, crack-free micropolygon meshes. • • determines surface tessellation along sub-patch edges using only properties of the edge. split sub-patches along non-isoparametric directions. Diag. Split Patch Control Points -Function (Ƭ) is used to define the tessellation factors for all patch edges. Uniformly diced using t-segments Wednesday, January 26, 2022 Uniform Tessellation Non-uniform tessellation is required: the edge is partitioned at its parametric midpoint 3 D Object vertices

30 Tessellation Algorithms • 3) Diag-Split Tessellation (Kayvon): - Wednesday, January 26, 2022

31 Outline 1 Tessellation: What & Why ? 2 Tessellation Patterns 3 Tessellation Algorithms 4 Fractional Tessellation 5 Next Step ? Wednesday, January 26, 2022

32 Tessellation Factors • Tessellation Factors are calculated according : • Polygon Size (number of pixels per polygon). • Position of polygon relative to the camera position. • local characteristics of the displacement map, as heights and normal variations ( for displacementmapped surfaces). For example : - projecting each triangle edge on the image plane and computing their screen-space lengths, giving larger weights to edges closer to the camera. Wednesday, January 26, 2022

33 Tessellation Factors Integer - Simpler - Produces an optimal triangulation. - - Fractional Harder to implement Support continuous Level Of Detail (LOD). Uses a mixture of regular meshes and transition regions. • Tessellation Factors may be for polygon (constant for all edges) or per-edge. • Remember, Integer Factors can be considered as a special case of Fractional Factors. Wednesday, January 26, 2022

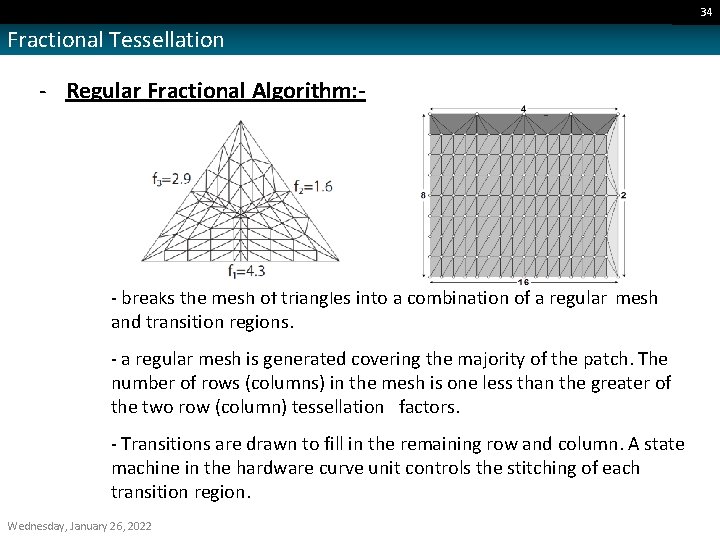
34 Fractional Tessellation - Regular Fractional Algorithm: - - breaks the mesh of triangles into a combination of a regular mesh and transition regions. - a regular mesh is generated covering the majority of the patch. The number of rows (columns) in the mesh is one less than the greater of the two row (column) tessellation factors. - Transitions are drawn to fill in the remaining row and column. A state machine in the hardware curve unit controls the stitching of each transition region. Wednesday, January 26, 2022

35 Fractional Tessellation - Regular Fractional Algorithm: For example, Triangle Fractional Algorithm: - equal tessellation weights f on all three edges: we obtain a regular inner triangle with tessellation factors f − 1. - different tessellation weights fi for each edge: The tessellation factor for the interior part can, for example, be chosen as maxi( fi)− 1. a) For the inner part, given an edge with tessellation factor f : 1) compute the integer part of f : n = f. └ ┘ 2) step n times with a step size 1/ f (assuming an edge length of one). 3) connect the current vertex with the midpoint of the edge. b) Then, stitch of each transition region. Wednesday, January 26, 2022

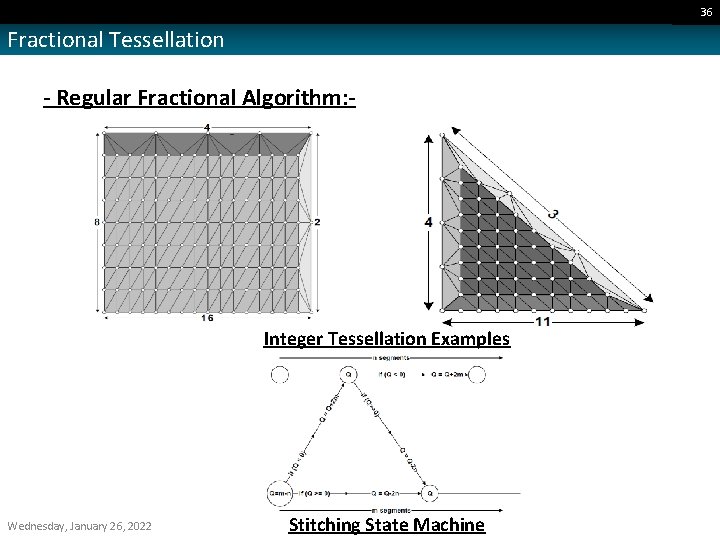
36 Fractional Tessellation - Regular Fractional Algorithm: - Integer Tessellation Examples Wednesday, January 26, 2022 Stitching State Machine

37 Fractional Tessellation - Non-Uniform Fractional Tessellation: - Jacob goals: 1) preserves the qualities of regular fractional tessellation, such as continuous level of detail. 2) strive for uniform micro triangle sizes in screen space ( not in camera space). - Given a base triangle, 1) tessellate using the regular fractional tessellation algorithm. 2) modify the barycentric coordinate of each vertex in the generated tessellation so that its projection in screen space results in uniform micro-triangle sizes by the reverse projection technique. Wednesday, January 26, 2022

38 Fractional Tessellation - Non-Uniform Fractional Tessellation: - Reverse Projection Technique: - - Let t’ denote a parameter along the line in camera space and t a parameter along the projection of the line in screen space. - Using similar triangles and linear interpolation in t and t’, we can derive a relationship between them as: Wednesday, January 26, 2022

39 Fractional Tessellation - Non-Uniform Fractional Tessellation: - Reverse Projection Technique: - than the mapping. Wednesday, January 26, 2022 - To have a uniform distribution of points in t (screen space). t’ varies according depth values Z 0 and Z 1. The bigger the depth difference, the more non-uniform distribution in t’. - Cons: - Extra computational power (11 instructions). - Uniform in screen space only if the base triangle is not undergoing any transformations other projection such as displacement

40 Outline 1 Tessellation: What & Why ? 2 Tessellation Patterns 3 Tessellation Algorithms 4 Fractional Tessellation 5 Next Step ? Wednesday, January 26, 2022

41 The Next Step ? • Gradual Tessellation ? ? ? Wednesday, January 26, 2022