Termodinmica de procesos irreversibles Hacia una teora de

Termodinámica de procesos irreversibles Hacia una teoría de los sistemas cerca del equilibrio: Onsanger

Primeras ideas sobre irreversibilidad • Si se desplaza un sistema del estado de equilibrio, sus parámetros varían con el tiempo. – Al cabo de un cierto tiempo, volverá a su estado inicial (debido a la 1ª Ley) • Relajación: proceso de pasar de un estado fuera del equilibrio a otro en equilibrio se denomina relajación. El tiempo asociado se designa como tiempo de relajación (τ=Tau) 10 -11 -2020 Dr. -Ing. fernando Corvalán Quiroz 2

Transformación cuasiestática • Si la velocidad en el proceso es mucho menor que la velocidad media de relajación para un parámetro A • Cuasiestática: Se dice que el parámetro A varía en forma infinitamente lenta, experimentando una serie de estados de equilibrio 10 -11 -2020 Dr. -Ing. fernando Corvalán Quiroz 3

Transformación no equilibrada • Si, por el contrario, la velocidad de variación del parámetro A con el tiempo es mayor o igual a la velocidad media de la relajación • Se trata de un proceso no-equilibrado 10 -11 -2020 Dr. -Ing. fernando Corvalán Quiroz 4

Termodinámica clásica y transformaciones irreversibles • El 2º principio de la Termodinámica persigue establecer la relación en las dos formas de transmitir energía (Q: calor; W: trabajo) – El paso de transformar calor en trabajo necesita de compensación, pero el proceso inverso no (progreso logrado a partir del primer tercio del siglo XX) 10 -11 -2020 Dr. -Ing. fernando Corvalán Quiroz 5

Compensación e irreversibilidad • Irreversible: el retorno del estado final al inicial es imposible sin efectuar algún cambio en el entorno. • Reversible: toda transformación cuasiestática es reversible, debido a que en todo instante el sistema se encuentra en equilibrio, y no se modificará el entorno 10 -11 -2020 Dr. -Ing. fernando Corvalán Quiroz 6

Algunos ejemplos de procesos irreversibles • En la ingeniería son por ejemplo importantes: – Todas las reacciones químicas – Cambios de fase rápidos (por ejemplo, la solidificación de un líquido subenfriado) – Difusión de dos gases, o de dos líquidos • …….

2° Principio para procesos irreversibles • Imaginemos dos estados de equilibrio de un sistema 1 y 2 – Supongamos que vamos de 1 a 2 por un proceso reversible • Luego se puede describir con diagramas de propiedades (ejemplo con dos grados de libertad) – Si de 2 a 1 volvemos a través de un proceso irreversible • No podemos representarlo en ningún diagrama

Luego, si aplicamos la 1° ley reversible irreversible no depende del camino Será >, <, o = a 0 ?

Diferencia nula • No puede ser, debido a que: – Significaría que un cambio irreversible podría llevarse a cabo de forma reversible sin modificar el entorno (medio ambiente) – Ya que devolvería al exterior un flujo de calor δQ i = δQ r y efectuaría un trabajo δW i = δW r – Si la transformación es irreversible, por definición, el proceso inverso exige compensación, modificando el entorno

Diferencia positiva • No puede ser, debido a: – Que el efecto global sería que el sistema absorbió una cantidad de calor δQ i - δQ r que se ha transformado completamente en un trabajo δW i - δW r , violando la 2° ley

La diferencia debe ser negativa • Debido a que: – Así se representa un ciclo en que primero se pasa de 1 a 2 (estados de equilibrio) por medios irreversibles absorbiendo Qi y realizando un trabajo Wi, para volver de 2 a 1 reversiblemente realizando un trabajo Wr sobre el sistema y este desprende un calor Qr – Luego el sistema entrega una cantidad de calor igual a δQ i - δQ r gracias a un trabajo exterior δW i - δW r , no contradiciendo la 2° ley.

Luego resulta la 2° ley de la termodinámica para procesos fuera del equilibrio • Teniendo en cuenta la siguiente ecuación • La diferencia anterior negativa, para una transformación adiabática irreversible (δQ=0), la entropía crece, es decir d. S > 0

Producción de Entropía • Se calcula (producción y flujo de S) a partir de la ecuación de Gibbs Potencial químico • Válida para condiciones de equilibrio Número de moles – Se postula que sigue siendo correcta para estados cerca del equilibrio. Depende de las mismas variables independientes que en los procesos de equilibrio

2 cantidades importantes: • Afinidad o fuerza generalizada: fuerza motriz , F, Por ejemplo, diferencias de temperaturas, velocidades, concentraciones • Flujo generalizado o velocidad: variación temporal de un parámetro extensivo, que caracteriza la respuesta del sistema a la fuerza aplicada, J, Por ejemplo, un calor transferido flujo afinidad

Luego, el flujo de entropía: • Es la suma de los productos de cada flujo por su afinidad correspondiente de cada proceso irreversible k que aporta a la producción de entropía: Mayor que cero

Afinidades y flujos: • Se supone que en un instante dado, los flujos dependen solamente del valor de las afinidades en ese momento – Parece que no tienen “memoria” – Raro, pero importantes aplicaciones parecen seguir este comportamiento (Fenómenos de Transporte) – En un momento dado t, el flujo de un proceso k, será igual al flujo a t=0 dada una afinidad inicial F 0, más lo que varía el flujo al variar las afinidades hasta el valor correspondiente, más otros términos….

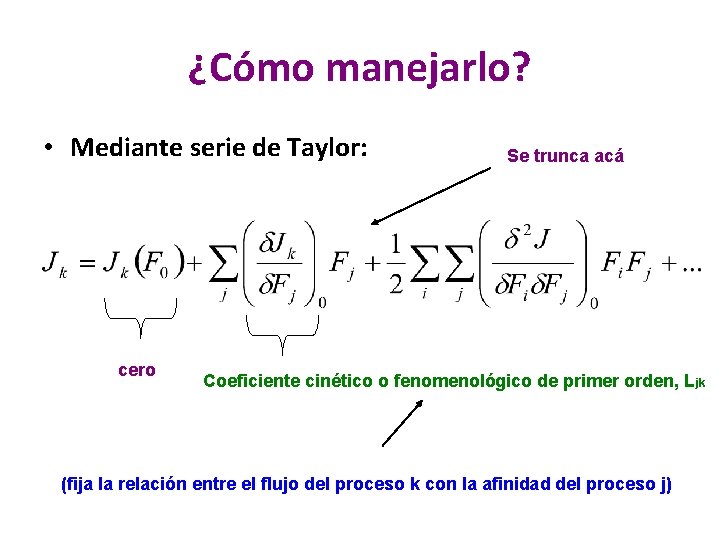
¿Cómo manejarlo? • Mediante serie de Taylor: cero Se trunca acá Coeficiente cinético o fenomenológico de primer orden, L jk (fija la relación entre el flujo del proceso k con la afinidad del proceso j)

Luego resulta • La ecuación que describe la dependencia del flujo, de cierta magnitud “extensiva” (función de la masa), asociado con el proceso irreversible k con la fuerza impulsora de este, tal que el proceso es lineal y “sin memoria” es

Teorema de Onsanger (1931) • Solamente reconocido un par de décadas mas tarde. – Expresa que cuando el flujo correspondiente al proceso irreversible i está influenciado por la afinidad Fj (fuerza impulsora del proceso irreversible j), entonces el flujo asociado al proceso j está influenciado por la afinidad Fi, a través del coeficiente de interferencia Lij

Teoría de las Fluctuaciones • Fluctuación: es la desviación de una magnitud de su valor en el equilibrio – Una vez producida, se dice que decae al proceso de volver al estado de equilibrio • Se supone que el decaimiento sigue las leyes lineales (recordar serie de Taylor truncada) • No olvidar que se está trabajando a escala macroscópica, y que d. S es positiva en cada región macroscópica del sistema

Bases teóricas del teorema de Onsanger • Se demuestra suponiendo válido el postulado de la reversibilidad microscópica – (tiempo t se reemplaza por – t) • Algunos autores, sobre todo Truesdell (1966) critican la suposición anterior. • La reconciliación de la reversibilidades macroscópica y microscópica es un tema relevante para la Mecánica Estadística