Termodinmica Aplicada AULA 5 Fernando Luiz Pellegrini Pessoa





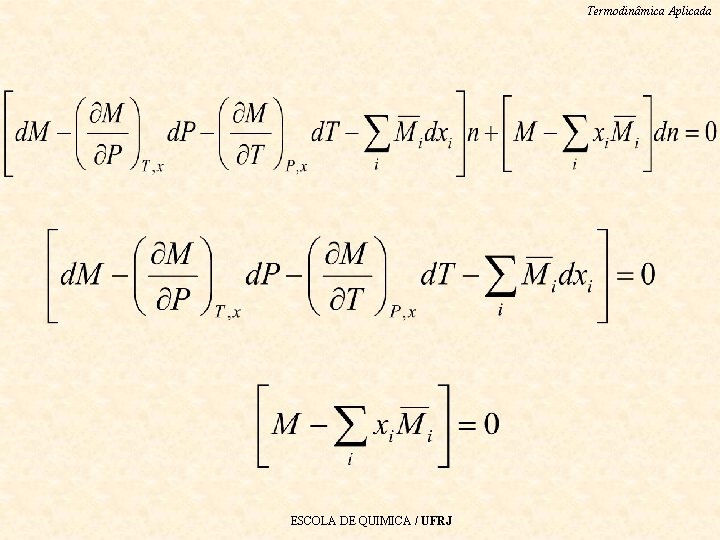

















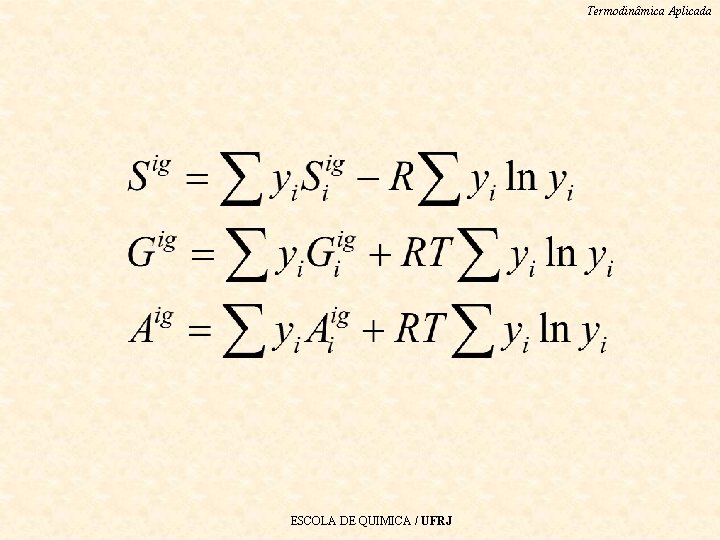


































- Slides: 61

Termodinâmica Aplicada AULA 5 Fernando Luiz Pellegrini Pessoa TPQBq ESCOLA DE QUÍMICA UNIVERSIDADE FEDERAL DO RIO DE JANEIRO ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada Propriedades parciais molares • Potential químico : • Significado físico da derivada na equação acima: Variação na energia de Gibbs decorrente da adição de uma quantidade (moles) infinitesimal de um componente i à mistura, mantendo-se constantes a temperatura, a pressão e todos os números de moles dos demais componentes. ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada Definição de Propriedades Parciais Molares M = U, H, A, S, V, G Pode-se calcular propriedades da solução a partir das propriedades parciais molares, bem como as propriedades parciais a partir das propriedades da solução ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada Propriedades utilizadas na TD de Soluções Propriedades de solução M, for ex. : U, H, S, G Propriedades parciais Propriedades das espécies puras Mi, for ex. : Ui, Hi , S i , G i ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada Equações Relacionando Propriedades Molares e Parciais Molares • Qualquer propriedade TD M: ESCOLA DE QUIMICA / UFRJ
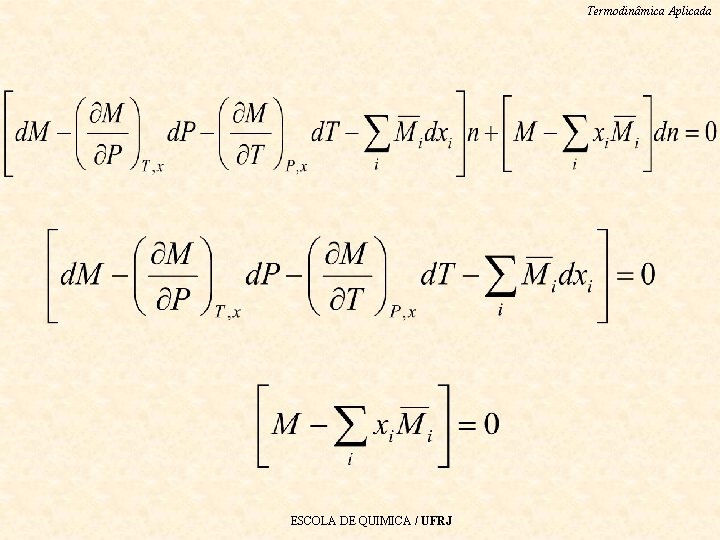
Termodinâmica Aplicada ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada Como calcular propriedades de mistura a partir de propriedades parciais ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada A partir de Obtém-se • Como Equação de Gibbs-Duhem (ela deve ser satisfeita para todas as variações em P, T e propriedade parcial, causada pela variação do estado em uma fase homogênea ) ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada Equação de Gibbs-Duhem A T e P constantes, a eq. de reduz a: • Se o sistema for binário: • ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada Observação importante A equação de Gibbs-Duhem é uma das mais importantes relações da termodinâmica clássica, pois permite obter a dependência das propriedades parciais molares com a composição, a T e P constantes. A equação de Gibbs-Duhem é muito utilizada para verificar a consistência de dados de propriedades parciais obtidos experimentalmente. ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada Esta equação é muito útil para checar dados experimentais. Se é cometido erros na medida experimental então os dados serão tipicamente termodinamicamente inconsistente. A única forma de afirmar que os dados experimentais são termodinamicamente consistente é aplicar a equação Gibbs-Duhem aos dados para ver se estes dados obedecem esta equação. Se não obedecem a equação, deve-se voltar e medir os dados novamente. Projetar alguma planta com base em dados errados pode complicar a sua vida!!!!!! ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada Relação entre propriedades de mistura e propriedades parciais ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada Para um sistema binário: ESCOLA DE QUIMICA / UFRJ

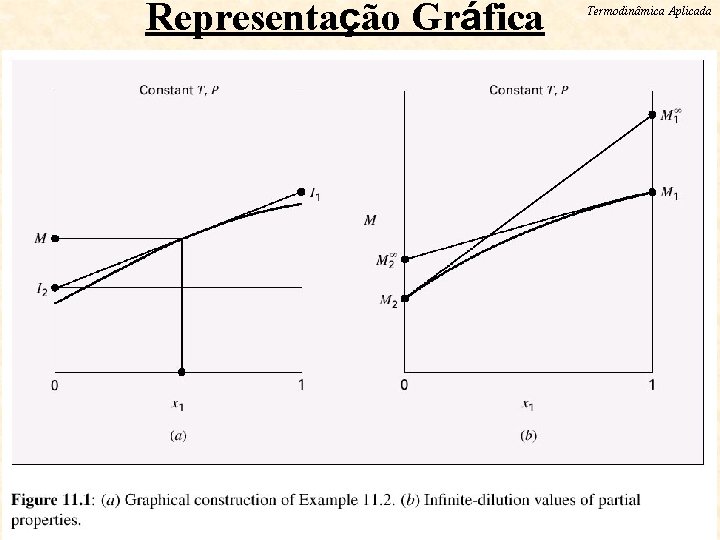
Representação Gráfica ESCOLA DE QUIMICA / UFRJ Termodinâmica Aplicada

Termodinâmica Aplicada O Potencial Químico O potencial químico é definido como a energia livre de • Gibbs parcial molar ESCOLA DE QUIMICA / UFRJ

Relações entre propriedades parciais: Termodinâmica Aplicada Toda equação que fornece uma relação • linear entre propriedades termodinâmicas de uma solução composição constante tem como sua contrapartida uma equação conectando as propriedades parciais molares da cada espécies na solução Exemplo H = U + PV então • ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada Mistura de Gases Ideais - habilidade limitada em descrever mistura • real - base conceitual para construir estrutura da • TD soluções - propriedade útil: • tem base molecular » aproxima-se da realidade em P=0 » analiticamente simples » ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada Coleção de partículas sem força • intermolecular e volume desprezível em relação ao volume molar Volume molar de um gás ideal: V = RT / P • ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada Para n moles de uma mistura de gases ideais: PV t = n. RT Considere ni moles de um gás ideal em Vt e T: • pi. Vt = ni. RT Logo p i = yi P • logo P = ∑ pi • onde pi é a pressão parcial • ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada Teorema de Gibbs: uma propriedade parcial molar (diferente do volume molar) de uma espécie constituinte de uma mistura de gases ideais é igual a propriedade molar da espécie correspondente como um gás ideal puro na T da mistura e na pressão igual a pressão parcial na mistura Isto é, para • Tem-se • ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada H de uma gás ideal independe de P Hiig (T, P) = Hiig (T, pi) • ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada Propriedades de misturas gases ideais Note que são propriedades que independem de P ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada • Mas, quando tomamos a entropia, que é dependente de P, este mesmo esquema não funciona. O que acontece com S quando voce mistura um gás ideal? Tem-se que d. Sig = Cpig d. T/T – Rd. P/P Gás ideal a T cte: d. Sig = - Rln. P Integrando de pi até P: Siig (T, P) – Siig (T, pi) = – Rln(P/pi) = Rln(xi) Logo Siig (T, pi) = Siig(T, P) – Rln(xi) ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada Siig (T, pi) = Siig(T, P) – Rln(xi) • Multiplicando por xi e aplicando ∑ obtém-se ESCOLA DE QUIMICA / UFRJ
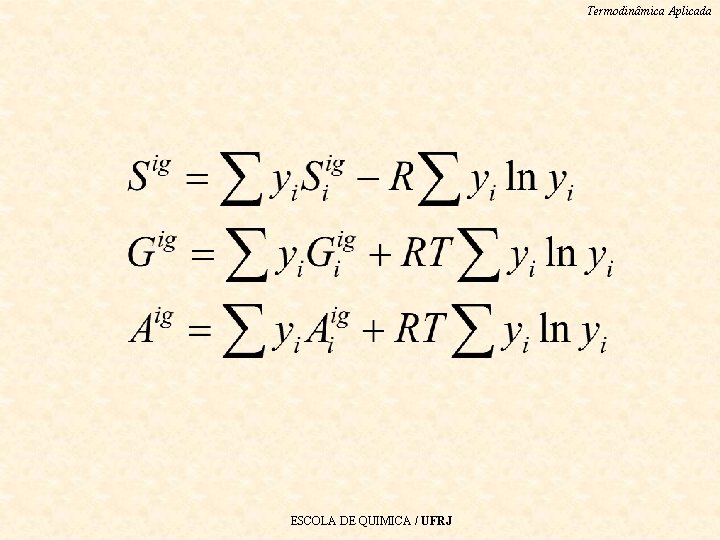
Termodinâmica Aplicada ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada Critério de Equilíbrio Para um sistema fechado onde existem fases em • equilíbrio, o critério geral de equilíbrio de fases impõe que o potencial químico de cada espécie presente seja igual em todas as fases. i=1, 2, . . . , NC ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada Observação importante A igualdade dos potenciais químicos foi o critério de equilíbrio estabelecido por Gibbs (mundo abstrato). Para voltar ao mundo real dos problemas físicos, Lewis introduziu o conceito de fugacidade, que é uma propriedade que pode ser fisicamente medida, e estabeleceu novo critério de equilíbrio: a igualdade entre as fugacidades. ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada Fugacidade e Coeficiente de Fugacidade de uma Substância Pura Para uma substância pura, a forma diferencial da energia livre de Gibbs é dada por A T constante: • Para um gás ideal: Logo, obtém-se: • • ESCOLA DE QUIMICA / UFRJ •

Termodinâmica Aplicada Fugacidade e Coeficiente de Fugacidade de uma Substância Pura Para que a equação anterior pudesse ser usada de • forma genérica, ou seja, para qualquer gás, Lewis propôs uma nova função, chamada FUGACIDADE (fi), análoga a pressão, dada por: Essa equação só é válida a T constante • A fugacidade tem as mesmas dimensões de pressão • Quando P* = 0 (gás ideal), tem-se que: • A razão adimensional fi/P é denominada de coeficiente de fugacidade e representada por: ESCOLA DE QUIMICA / UFRJ •

Termodinâmica Aplicada Fugacidade e Coeficiente de Fugacidade de uma Substância Pura Para se calcular os valores numéricos de fi a partir dos dados PVT de uma substância pura, a T constante, a seguinte equação deve ser usada: • é volume molar do gás ideal é o volume residual Para um gás ideal, o volume residual é zero em qualquer T e P. Logo, se ESCOLA DE QUIMICA / UFRJ •

Termodinâmica Aplicada ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada • Forma alternativa: • Gases ideais: • Fluidos reais: • Combinando as duas eqs: ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada Correção de Poynting • Podemos calcular fugacidade ou coeficiente de fugacidade em altas pressões relacionando-os com os valores na saturação. – Para gases, podemos calcular a fugacidade integrando de zero até a saturação. – Na saturação (equilíbrio líquido-vapor, sabemos que ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada Em altas pressões para a fase líquida, temos que fazer a integração na pressão para obter uma expressão para em relação à obtendo-se ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada a equação relaciona o coeficiente de fugacidade saturado (gás ou líquido) com a fugacidade de um líquido comprimido. A exponencial é chamda fator de Poynting ou o fator de correção de Poynting correction factor, que é bastante usado. ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada Fugacidade e Coeficiente de Fugacidade de um Componente i na Mistura • Para o gás ideal: • Por analogia, define-se para uma espécie em solução: ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada Fugacidade e Coeficiente de Fugacidade de um Componente i na Mistura Analogamente, para um componente i na mistura, a T • constante, tem-se ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada Notação Observação: A notação usada introduz o símbolo “^” ao invés da barra “-“, porque a fugacidade do componente i na mistura não é a propriedade parcial de f e o coeficiente de fugacidade do componente i na mistura não é a propriedade parcial de . ESCOLA DE QUIMICA / UFRJ •

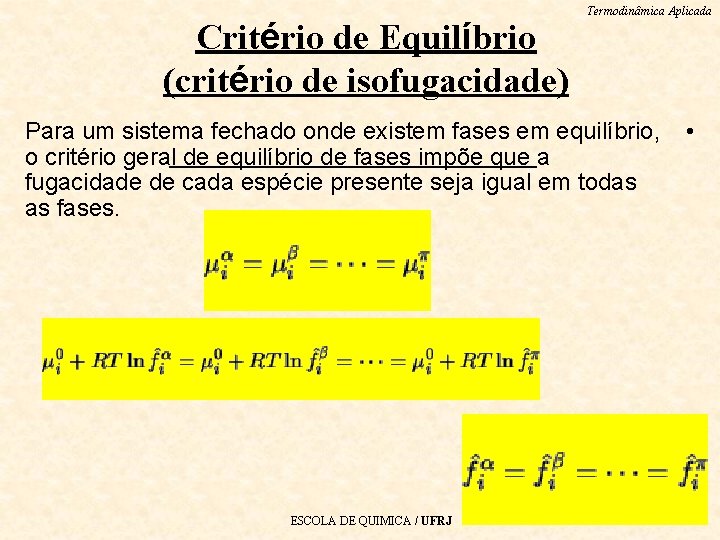
Critério de Equilíbrio (critério de isofugacidade) Termodinâmica Aplicada Para um sistema fechado onde existem fases em equilíbrio, o critério geral de equilíbrio de fases impõe que a fugacidade de cada espécie presente seja igual em todas as fases. ESCOLA DE QUIMICA / UFRJ •

Termodinâmica Aplicada Relação Fundamental – Propriedade residual • Todas as equações aplicadas a qualquer propriedade termodinâmica M pode também ser aplicada a qualquer propriedade residual correspondente MR. Pode-se escrever • Como medir entropia? Eliminar da equação: ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada Esta é a relação fundamental e pode ser utilizada para calcular outras propriedades. Para T e x constantes: A Propriedade parcial de GR ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada • G R: ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada Equação Virial truncada após segundo termo: ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada Note que esta equação é válida apenas para P baixas e moderadas. Não é válida para líquido. Para uma mistura binária: Para uma mistura multicomponente ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada Regra de combinação: com ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada Prausnitz: ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada Calculando fugacidade com EE: ou. A propriedade parcial pode ser usada para calcular: ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada Fugacidade e Propriedade Parcial O logaritmo neperiano da razão entre a fugacidade do componente i na mistura e a sua fração molar é a propriedade parcial de ln f , dado por • Fazendo-se M = ln f, todas as expressões vistas • anteriormente para as propriedades parciais molares são aplicáveis: ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada Coeficiente de Fugacidade e Propriedade Parcial Analogamente, tem-se que o logaritmo neperiano do • coeficiente de fugacidade do componente i na mistura é a propriedade parcial de ln , dado por Fazendo-se M = ln , todas as expressões vistas • anteriormente para as propriedades parciais molares são aplicáveis: ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada Observação importante O maior uso da fugacidade é na solução de problemas de equilíbrio de fases. Nesses problemas, a composição das fases é geralmente a propriedade que se quer determinar, o que necessita do conhecimento da dependência da fugacidade com a composição. Embora esse conhecimento possa ser determinado experimentalmente, a termodinâmica impõe certas restrições quanto à natureza dessa dependência. Essas restrições levaram à definição de novas funções termodinâmicas, como o coeficiente de atividade e a energia livre de Gibbs em excesso, para facilitar o tratamento dos dados experimentais. ESCOLA DE QUIMICA / UFRJ

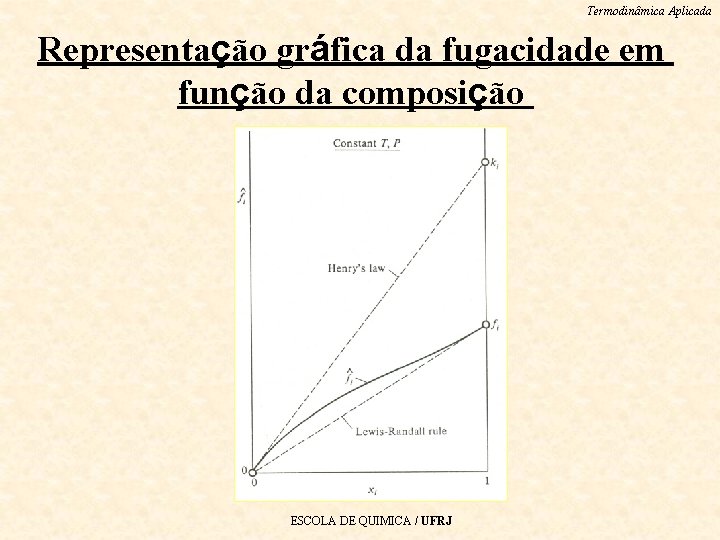
Termodinâmica Aplicada Representação gráfica da fugacidade em função da composição ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada Limites da fugacidade para xi = 0 e xi = 1 Lei de Henry: estabelece que , quando xi=0 e a • inclinação da reta tangente à curva é a constante de Henry ki. Regra de Lewis-Randall: expressa a exigência • termodinâmica de que e sua derivada em relação a xi tornam-se iguais à fugacidade do componente i puro (fi) no limite em que xi 1. ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada Lei de Henry e Regra de Lewis-Randall As linhas retas da figura anterior que representam a Lei • de Henry e a Regra de Lewis-Randall podem ser expressas, respectivamente, pelas seguintes equações: ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada Observação importante (I) As equações que expressam a Lei de Henry e a Regra de Lewis-Randall têm formas similares, mas “ki” e “fi” têm valores experimentais geralmente diferentes. Ambas as equações representam linhas retas no gráfico de. A termodinâmica impõe a restrição de que a curva seja tangente a essas 2 retas nos limites de xi = 0 e xi = 1, e a natureza dessa curva entre esses limites deve ser determinada experimentalmente. Devido à forma logarítmica das equações que a define, a fugacidade é sempre positiva. Além disso, a termodinâmica restringe que a inclinação seja sempre positiva para um fluido estável. ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada Observação importante (II) A Lei de Henry e a Regra de Lewis-Randall são representações idealizadas que geralmente não conseguem descrever a dependência de com a composição para uma grande faixa de fração molar. Contudo, elas representam aproximações satisfatórias para soluções suficientemente diluídas ou concentradas na espécie i. Será visto mais adiante que o conceito de solução ideal se inspirou na Lei de Henry e na Regra de Lewis-Randall e exerceu papel fundamental no desenvolvimento de métodos para uma representação adequada das propriedades das soluções reais. ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada • O que faz uma IDEAL solução ideal? Comparando solução ideal com gás ideal? – Como deveria ser as interações energéticas de uma solução ideal? • Compare estas com as interações do gás ideal. • Como deveria ser as interações volume/forma/tamanho de uma solução ideal? • Compare estas interações volume/forma/tamanho em um gás ideal. Uma mistura de gases ideais é uma mistura ideal? ESCOLA DE QUIMICA / UFRJ • •

Termodinâmica Aplicada Soluções ideais: 1. Ela serve como padrão para uma solução real ser comparada. 2. Seu comportamento é de uma solução. 3. Comtém moléculas de tamanho e natureza químca semelhantes, exemplo, isômeros seguindo a definição de fugacidade, e com o estado padrão como líquido puro nas mesmas P e T ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada Solução ideal O modelo de solução ideal serve como base para • descrever de forma aproximada o comportamento de uma solução real (não-eletrolítica). O modelo de solução ideal fornece a dependência da • fugacidade dos componentes na solução com a composição. Considere o modelo representado pela regra de Lewis- • Randall: ESCOLA DE QUIMICA / UFRJ

Termodinâmica Aplicada Regra Lewis-Randall para solução ideal O coeficiente de fugacidade de uma solução ideal é obtido dividindo a regra de Lewis. Randall por xi P • ESCOLA DE QUIMICA / UFRJ