Terminology Shift Cipher Number Theory rings Classical Ciphers

- Terminology - Shift Cipher - Number Theory: rings Classical Ciphers – I CSCI 284 Spring 2004 GWU CS 284/Spring 04/GWU/Vora/Classical Ciphers

From Schneier Some terminology A sender encrypts a plaintext message to get ciphertext which is sent to the receiver who decrypts it to obtain the plaintext. e(P) = C d(C) = P d(e(P)) = P; d e = I e one-to-one For the application of secret communication between two parties, it should not be possible for an eavesdropper to decrypt the message. i. e d should be easy for the (legitimate) receiver, not for anyone else. 2/6/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 2

From Schneier: Some terminology - contd. • Cipher: is the cryptographical algorithm/mathematical function used to encrypt • A restricted cipher is one whose security depends on keeping the algorithm secret. Inadequate, because doing so does not provide a systematic way of simulated attack/vulnerability analysis by external experts - which typically improves security. 2/6/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 3

From Schneier: Some terminology - contd. • A key is used as a parameter in some ciphers. The security of ciphers that use keys is based on keeping the key(s), and not the cipher, secret. e. K 1(P) = C; d. K 2(C) = P • Keyspace: set of all possible keys. • Cryptosystem: algorithm + all ciphertexts + all plaintexts + all keys 2/6/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 4

From Stinson Formal definition: cryptosystem A cryptosystem consists of: P set of all plaintext C set of all ciphertext K set of all keys E set of encryption rules, e. K: P C D set of decryption rules d. K : C P d. K e. K(x) = x d. K e. K invertible and inverses of each other 2/6/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 5

Typical Scenario • Alice and Bob randomly choose a key, K K when they are unobserved or communicating on a secure channel • If Alice wants to send Bob a message, x 1 x 2 x 3 x 4…xn She sends: y 1 y 2 y 3 y 4…yn Where yi = e. K(xi) xi is a symbol from the alphabet 2/6/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 6

Encryption is an invertible function Need inversion to be somewhat easier than a lookup table, because both Alice and Bob would need the entire lookup table 2/6/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 7

One possibility • Alice and Bob agree on two time zones: say Pacific time and Eastern time. • Encryption means taking a time from the Eastern to the Pacific zone; decryption is vice versa. • Encryption of 4 is 4 -3 = 1 • Decryption of 1 is 1+3 = 4 • If you don’t know what the chosen time zones are, the encryption protects the data 2/6/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 8

Shift Cipher P = C = K = Zm e. K(x) = (x+K) mod m d. K(y) = (y-K) mod m e 3(2) = (2+3) mod 4 = m = 12 time in UK given time on US east coast: e 5(3) = 8 mod 12 time on US east coast given time in UK: d 5(1) = 8 mod 12 2/6/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 9

Shift Cipher Don’t need entire lookup table, only the value 5 2/6/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 10

Zm Definition: a b (mod m) m divides a-b Zm is the “ring” of integers modulo m: 0, 1, 2, …m-1 with normal addition and multiplication, performed modulo m We define a mod m to be the unique remainder of a when divided by m, i. e. a mod m Zm 2/6/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 11

Properties of Zm (definition of a ring) • Closed under addition and multiplication If a, b Zm then a+b, ab Zm • Addition and multiplication are commutative and associative If a, b Zm then a+b = b+a ab = ba (a+b)+c = a +(b+c) and (ab)c = a(bc) 2/6/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 12

Properties of Zm – contd. • Additive and multiplicative identities in Zm Additive identity is 0 mod m Multiplicative identity is 1 mod m • Distributive property holds For a, b, c Zm (a+b)c = ac + bc and a(b+c) = ab + ac 2/6/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 13

Properties of Zm – contd. • Additive inverse? A number y such that x + y = x for all x in Zm • Multiplicative inverse? A number y such that x*y = 1 for all x in Zm 2/6/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 14

Shift cipher on English alphabet A 0 B 1 C 2 D 3 E 4 F 5 G 6 H 7 I 8 J 9 K L M N 10 11 12 13 O P Q R S T U V W X Y Z 14 15 16 17 18 19 20 21 22 23 24 25 Key = k (add 10, so A goes to 10, i. e. k) ABCDEFGHIJKLMNOPQRSTUVWXYZ klmnopqrstuvwxyzabcdefghij 2/6/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 15

Do in class 1. 1 from text – – 7503 mod 81 -7503 mod 81 81 mod 7503 -81 mod 7503 1. 2 from text Suppose a, m > 0 and a 0 (mod m) Prove that (-a) mod m = m – (a mod m) 1. 5 from text. Decrypt (encrypted with a shift cipher): beeakfydjxuqyhyjiqryhtyjiqfbqduyjiikfuhcqd 2/6/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 16

From Schneier Some terminology - Cryptanalysis • Cryptanalysis is an (usually vulnerability) analysis of a cipher. • Loss of key through means other than cryptanalysis (storage of key in an insecure fashion, for example) is a compromise. • An attempt at cryptanalysis is an attack Kerckhoff’s assumption is that security resides entirely in the key, i. e. cipher not restricted in any way. This assumption is useful for external/open vulnerability analysis of different ciphers and for determining their security. 2/6/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 17

From Schneier Cryptanalysis - types of attacks • Known-plaintext: m and c known When a known message/expected message is encrypted, as in file headers in known file-types (jpeg, tiff) • Chosen-plaintext: m chosen by attacker Attacker manages to make naïve encrypter encrypt a chosen message • Adaptive-chosen-plaintext: m chosen by attacker as attack proceeds • Chosen-key: k chosen 2/6/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 18

From Schneier Cryptanalysis - types of attacks – contd. • Ciphertext-only: c known Any eavesdropping/wire tapping/message interception • Chosen-ciphertext: c chosen by attacker (as when the attacker has access to the decryption, for example DVD players for watermarking, or decrypting of a message encrypted with a public key) • Rubber-hose (Physical threat to key-holder) 2/6/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 19

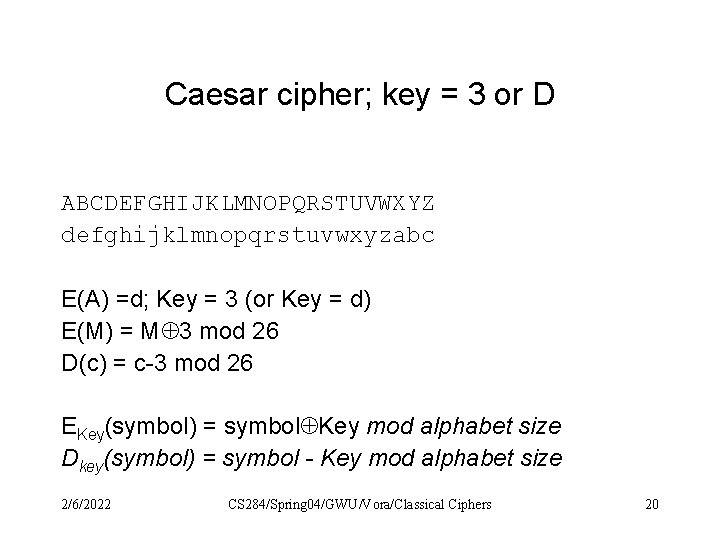
Caesar cipher; key = 3 or D ABCDEFGHIJKLMNOPQRSTUVWXYZ defghijklmnopqrstuvwxyzabc E(A) =d; Key = 3 (or Key = d) E(M) = M 3 mod 26 D(c) = c-3 mod 26 EKey(symbol) = symbol Key mod alphabet size Dkey(symbol) = symbol - Key mod alphabet size 2/6/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 20

Shift cipher - cryptanalysis • Deciphering exactly one symbol in the ciphertext is enough to break the cipher. Serious weakness. • Can decipher by targeting specific statistical properties of the language of the message – for example, single-lettered words in english can only be “a” or “I” • Can decipher easily by brute-force, need to try only 26 keys. 2/6/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 21

Cryptanalysis of Shift Cipher On a shift cipher encrypted message, alphabet of size n, determine the Average case complexity (n-1)/2 and Worst-case complexity (n-1) Of a brute force attack 2/6/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 22

Shift cipher – weaknesses and strengths • Strengths: – Computationally efficient to encrypt and decrypt – No storage requirements – Ciphertext not longer than plaintext • Weaknesses: – Vulnerable to brute force: a given ciphertext can correspond to only 26 messages (or messages equal to the length of the alphabet) – Even more vulnerable when the language has statistical properties, because some keys will be quickly apparent as unlikely/impossible given ciphertext 2/6/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 23

Shift cipher - Lessons learnt • Need cipher that takes more keys than length of language alphabet, so brute force is more difficult • Key should not be determinable from decrypting a single symbol • How about two variables in the key, not 1? 2/6/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 24