Terleti fejlettsgi klnbsgek mrse dr Jeney Lszl egyetemi

Területi fejlettségi különbségek mérése dr. Jeney László egyetemi adjunktus jeney@caesar. elte. hu Regionális és környezeti elemzési módszerek I. BME Regionális és környezeti gazdaságtan mesterszak (MSc) 2013/2014, II. félév BCE Gazdaságföldrajz és Jövőkutatás Tanszék

Területi egyenlőtlenségi vizsgálatok jelentősége n Területi elemzések alapkérdése: egyenlőtlenségek vizsgálata – – – n Mekkorák az egyenlőtlenségek? Nagy vagy kicsi? Hogyan alakul? Nő vagy csökken? Mi az oka ezen folyamatoknak? A népesség és a gazdaság térben egyenlőtlenül helyezkedik el, okai: – – – Eltérő természetföldrajzi adottságok Erőforrások szórtsága Eltérő történelmi fejlődésmenet 2

Területi különbség és területi egyenlőtlenség n Nem azonosság: 1. Különbség 2. Egyenlőtlenség 1. Területi különbség, differenciáltság („differentiation”) – – 2. Területi egyenlőtlenség („inequality”) – – n Pusztán térben különböző előfordulás Pl. természetföldrajzi eltérések, területi specializáció Különbségek mentén társadalmi értéktartalom is megjelenik Pl. jövedelmi, egészségügyi eltérések Differenciáltsághoz is kötődhet értéktartalom diverzitás, mint egyenlőtlenségi kategória – – – Ökológia: faji sokszínűség Közgazdaságtan: gazdasági tevékenységek sokszínűsége 3 Társadalomkutatás: multikulturalitás (XX. sz. : „diverzitás sz-a”)

Kiegyenlítettség ≠ kiegyenlítődés n Állapotjellemzők (statikus szemlélet): mekkora az egyenlőtlenség (nagy–kicsi)? – Differenciáltság–kiegyenlítettség n Változás iránya (dinamikus szemlélet): hogyan változik az egyenlőtlenség (növekszik– csökken)? – Differenciálódás–kiegyenlítődés (utóbbit soha nem éri el teljesen, helyette inkább közeledés, különbségek csökkenése) – Divergencia vagy konvergencia 4 – Polarizáció, tagolódás vagy nivelláció

Területi elemzések legvitatottabb kérdésköre n 1. Vizsgálati különbségek területi egyenlőtlenségek eltérő megítélése Tárgy – Település, járás, megye, régió, nagyrégió – Városok: székhelyek, városok, városias karakterű települések, nagy népességű települések 2. Mérték, mutatószám – Írni-olvasni tudók, diplomások, átlagosan elvégzett osztályszám 3. Térségi szint, aggregáltság – Település, városkörzet, megye 4. Egyenlőtlenségi mutató – Range-típusú mutatószámok vagy relatív szórás 5. Időtáv – Rövidebb vagy hosszabb 5
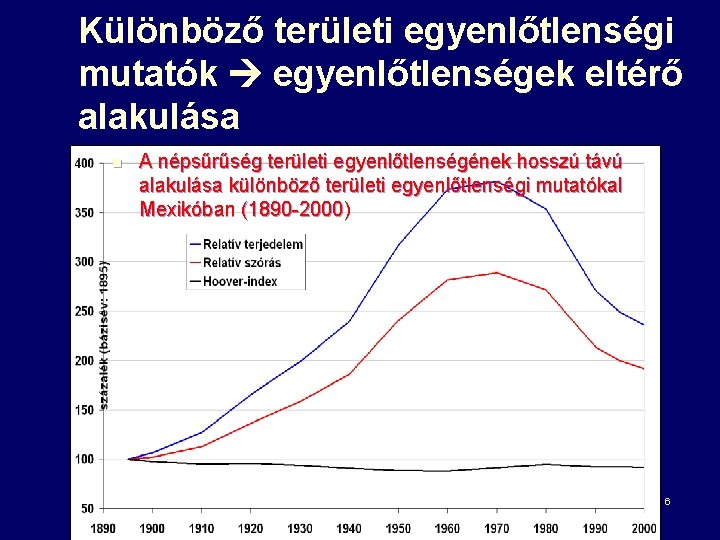
Különböző területi egyenlőtlenségi mutatók egyenlőtlenségek eltérő alakulása n A népsűrűség területi egyenlőtlenségének hosszú távú alakulása különböző területi egyenlőtlenségi mutatókal Mexikóban (1890 -2000) 6
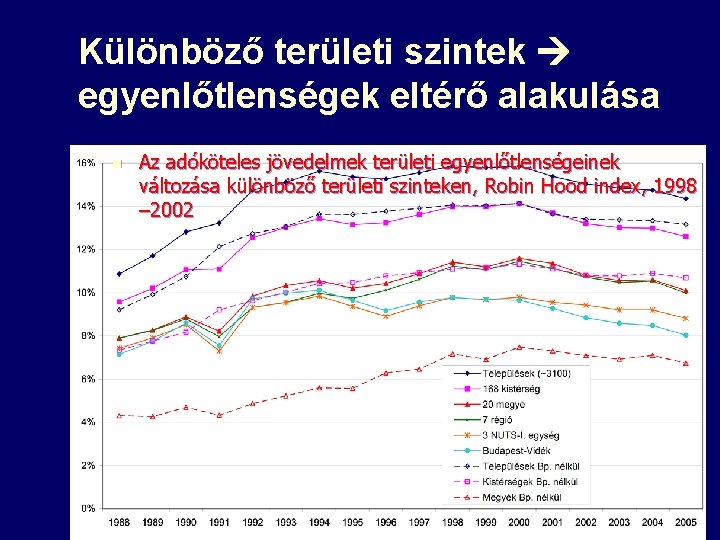
Különböző területi szintek egyenlőtlenségek eltérő alakulása n Az adóköteles jövedelmek területi egyenlőtlenségeinek változása különböző területi szinteken, Robin Hood index, 1998 – 2002 7

Megoldások a területi egyenlőtlenségi vizsgálatok eltérő eredményeire n Egyidejűleg van jelen a kiegyenlítődés és a differenciálódás – Egyes szférák, térségi szintek polarizálódnak, mások homogenizálódnak n Összetett közelítés, többfajta tesztelés – – – n Választott közelítés egyértelmű meghatározása – – n Többfajta mutatószám Többfajta egyenlőtlenségi index Többfajta térségi szint Milyen egyenlőtlenségi mutatót választunk? Milyen térségi szintre vonatkozik a mérés? Mi a vizsgált jelenség? Mi a vizsgálat időtávja? Nem minden közelítés azonos súlyú, fontosságú 8

Területi egyenlőtlenségi indexek n Sokféle egyenlőtlenségi index, mutatószám létezik – P. B. Coulter (1989): 50 különböző egyenlőtlenségi index n Jellemzőik – – – Folytonosság Nem-negativitás: ha nincs egyenlőtlenség indexérték=0 Monotonitás: nagyobb egyenlőtlenség nagyobb indexérték Identitás: azonos eloszlásnál azonos indexérték Szimmetria: „A” annyira különbözik „B”-től, mint „B” „A”-tól 9

Területi egyenlőtlenségek mérésére szolgáló statisztikai eszközök n Területi egyenlőtlenségi indexek, leggyakrabban használtak: – A területi polarizáltság mérőszámai n n Relatív terjedelem/Relatív range (Q) Duál mutató/Éltető–Frigyes index (D) – Szórás-típusú területi egyenlőtlenségi indexek n Súlyozott relatív szórás (V) – Területi eloszlást mérő egyenlőtlenségi indexek n n Hirschman–Herfindahl index (K) Hoover-index/Krugman-index (H) – Területi egyenlőtlenségek összetettebb mérési módszerei n n n Gini együttható (G) Távolságfüggvények Korrelációs mérőszámok 10

Melyik területi egyenlőtlenségi indexet használjuk? n Meghatározó: – Vizsgálati kérdés – Rendelkezésre álló adatbázis n n Sok esetben több index kiszámítása szükséges Jobb: – Korlátos (normalizált) index: véges értékkészlet (zárt intervallum: szélsőértékekhez viszonyíthatjuk) szórás típusú mutatók hátránya n Nem kötődik közvetlenül a térbeliséghez – Területi egyenlőtlenségi indexek többsége nem csak a területi egyenlőtlenségek mérésére használható (pl. társadalmi csoportok, ágazatok közötti egyenlőtlenségekre is) – Egyenlőtlenségi mutató azonos akár ellentétes térbeli 11 konfigurációnál is

σ konvergencia n A szórás értékeinek időrendbe állítása (általában relatív szórás és súlyozott relatív szórás értékeinek) – Tágabb értelemben: bármely területi egyenlőtlenségi mutató értékeinek időrendbe állítása – Csökkenő trend esetén: σ konvergencia n Nem tévesztendő össze a β konvergenciával – Adott mutató értékváltozása és értékeinek nagysága közötti összefüggés iránya alapján – Negatív β érték: β konvergencia 12
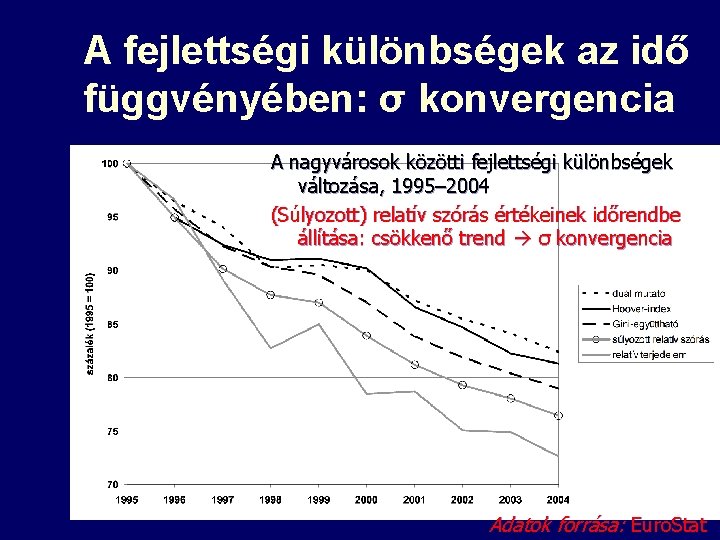
A fejlettségi különbségek az idő függvényében: σ konvergencia A nagyvárosok közötti fejlettségi különbségek változása, 1995– 2004 (Súlyozott) relatív szórás értékeinek időrendbe állítása: csökkenő trend σ konvergencia 13 Adatok forrása: Euro. Stat
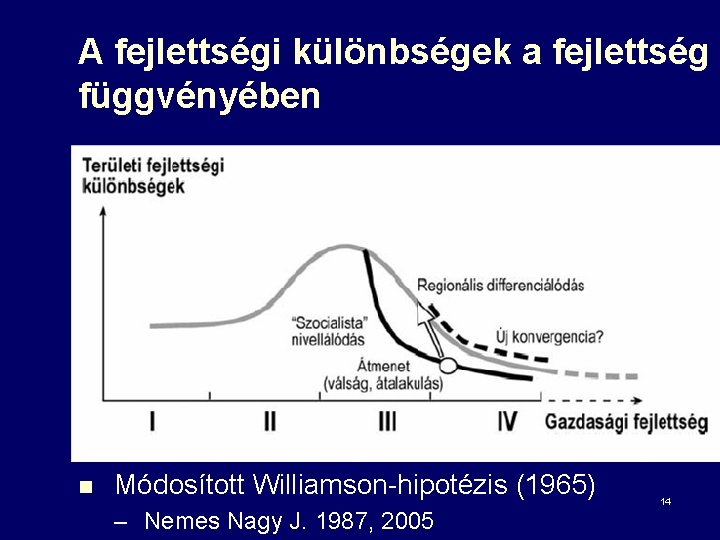
A fejlettségi különbségek a fejlettség függvényében n Módosított Williamson-hipotézis (1965) – Nemes Nagy J. 1987, 2005 14

A fejlődés a fejlettség függvényében: β konvergencia A nagyvárosok fejlettsége (1995) és fejlődése (1995– 2004) közötti összefüggés Adott mutató értékváltozása és értékeinek nagysága közötti összefüggés iránya alapján Negatív β érték β konvergencia 15 Adatok forrása: Euro. Stat

A területi koncentráció mérése: Hirschman–Herfindahl index

Hirschman–Herfindahl index n n n Egy jelenség földrajzi koncentrációjának mérésére használt mutatószám Csak összegezhető (nem fajlagos) mutatóra számítható Képlete – Xi = nem fajlagos mutató i régióban – Σxi = nem fajlagos mutató a teljes régióban n Értékkészlete: 1/n ≤ K ≤ 1 – Minél nagyobb az értéke, annál nagyobb az egyenlőtlenség – Előfordulhat, hogy alacsonyabb területi szinten csökken az értéke n Mértékegysége: nincs 17

Hirschman–Herfindahl index kiszámításának lépései 1. 2. 3. Összegezzük a vizsgált adatsort Minden térség esetében elosztom az adott térség értékét az előbb kiszámított összeggel (Excel $) Minden térség esetében a kapott hányadosokat négyzetre emelem (Excel jobb oldali Alt+3 együtt, majd 2 = ^2) – 2– 3. lépések egy oszlopban is megoldhatók 4. Az így kapott értékeket összegzem 18
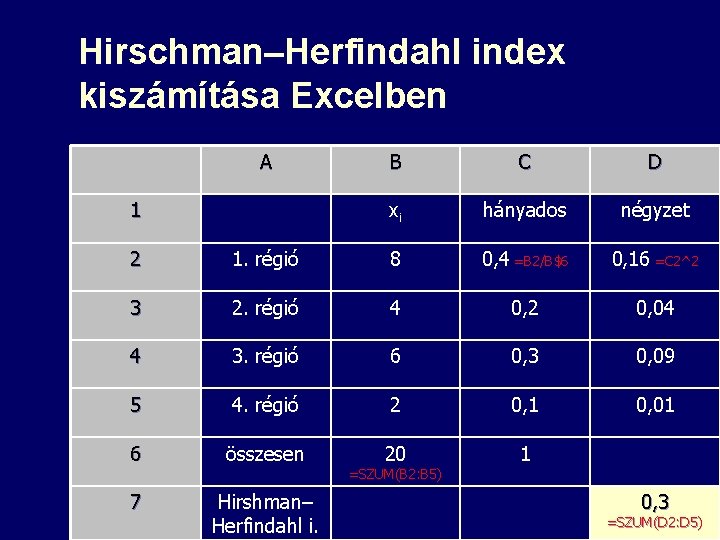
Hirschman–Herfindahl index kiszámítása Excelben A 1 B C D xi hányados négyzet 2 1. régió 8 0, 4 =B 2/B$6 0, 16 =C 2^2 3 2. régió 4 0, 2 0, 04 4 3. régió 6 0, 3 0, 09 5 4. régió 2 0, 1 0, 01 6 összesen 20 1 7 Hirshman– Herfindahl i. =SZUM(B 2: B 5) 0, 319 =SZUM(D 2: D 5)
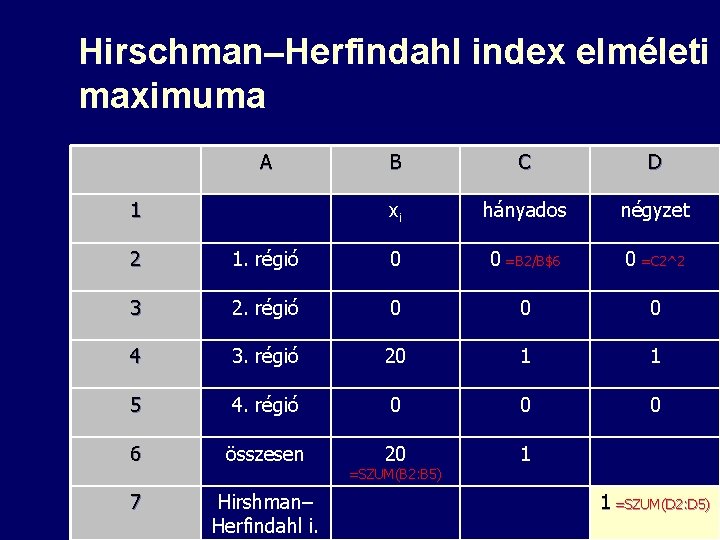
Hirschman–Herfindahl index elméleti maximuma A 1 B C D xi hányados négyzet 2 1. régió 0 0 =B 2/B$6 0 =C 2^2 3 2. régió 0 0 0 4 3. régió 20 1 1 5 4. régió 0 0 0 6 összesen 20 1 7 Hirshman– Herfindahl i. =SZUM(B 2: B 5) 20 1 =SZUM(D 2: D 5)
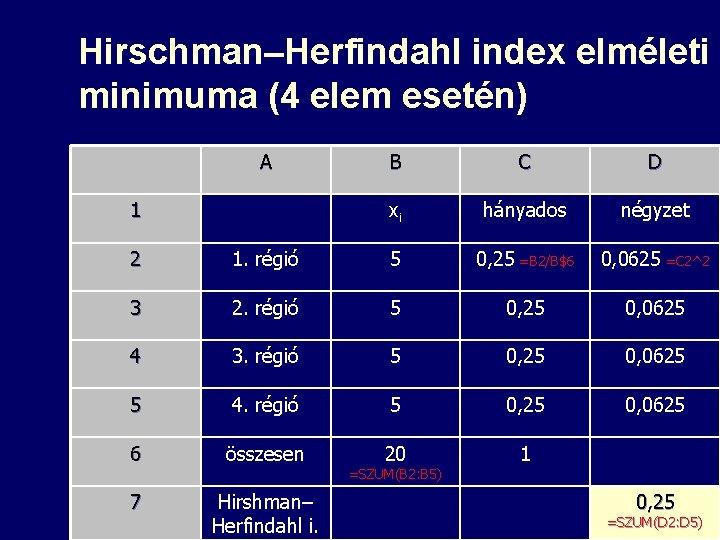
Hirschman–Herfindahl index elméleti minimuma (4 elem esetén) A 1 B C D xi hányados négyzet 2 1. régió 5 0, 25 =B 2/B$6 0, 0625 =C 2^2 3 2. régió 5 0, 25 0, 0625 4 3. régió 5 0, 25 0, 0625 5 4. régió 5 0, 25 0, 0625 6 összesen 20 1 7 Hirshman– Herfindahl i. =SZUM(B 2: B 5) 21 0, 25 =SZUM(D 2: D 5)

Területi eloszlások összevetése: Hoover index

Hoover index n n Egyik legelterjedtebb, legáltalánosabban használt területi egyenlőtlenségi index Két mennyiségi ismérv területi megoszlásának eltérését méri – Az egyik ismérv, társadalmi-gazdasági jelenség mennyiségének hány százalékát kell a területi egységek között átcsoportosítani ahhoz, hogy területi megoszlása a másik jellemzőével azonos legyen – Területi kutatásokban leggyakrabban a népesség területi eloszlásával vetjük össze más társadalmi-gazdasági ismérvével n n 1941: E. M. Hoover, amerikai agrárközgazdász Használja a földrajz, szociológia, közgazdaságtan, ökológia is 23

Hoover index n Két nem fajlagos mutató területi megoszlása közötti eltérést mérhetjük vele – Egy fajlagos mutató számlálója és nevezője között is lehet n Képlete: – xi = i régió részesedése x nem fajlagos mutatóból – yi = i régió részesedése y nem fajlagos mutatóból n xi és yi: két megoszlási viszonyszám, melyekre fennállnak az alábbi összefüggések – – n n Σxi = 100 Σyi = 100 A mutató szimmetrikus, a két összevetett megoszlás (xi és yi) szerepe, sorrendje felcserélhető Értékkészlete: 0 ≤ H ≤ 100 – Minél nagyobb az értéke, annál nagyobb az egyenlőtlenség 24 n Mértékegysége: %

Hoover index kiszámításának lépései 1. 2. 3. 4. Mindkét nem fajlagos mutató adatsorának értékeit összegezzük Minden térség esetében kiszámítjuk az adott térség százalékos részesedését az összes mennyiségből (mindkét mutató esetében) Minden térség esetében kivonjuk az egyik mutató szerinti százalékos részesedésből a másik mutató szerinti százalékos részesedést Minden térség esetében az így kapott különbségek abszolút értékét vesszük (ABS) – 2– 4. lépések egy oszlopban is megoldhatók 5. 6. Az abszolút értékeket összegzem A kapott összeg értékét megfelezem 25
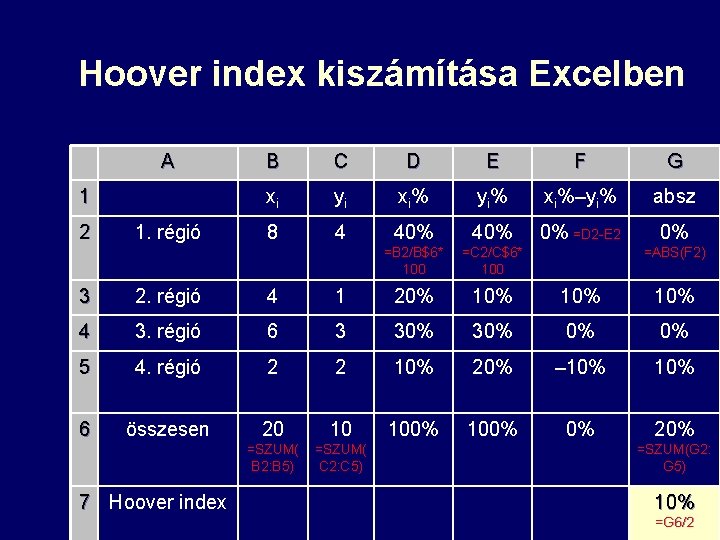
Hoover index kiszámítása Excelben A 1 2 1. régió B C D E F G xi yi xi% yi% xi%–yi% absz 8 4 40% 0% =D 2 -E 2 0% =B 2/B$6* 100 =C 2/C$6* 100 =ABS(F 2) 3 2. régió 4 1 20% 10% 10% 4 3. régió 6 3 30% 0% 0% 5 4. régió 2 2 10% 20% – 10% 6 összesen 20 10 100% 0% 20% =SZUM( B 2: B 5) =SZUM( C 2: C 5) 7 Hoover index =SZUM(G 2: G 5) 26 10% =G 6/2
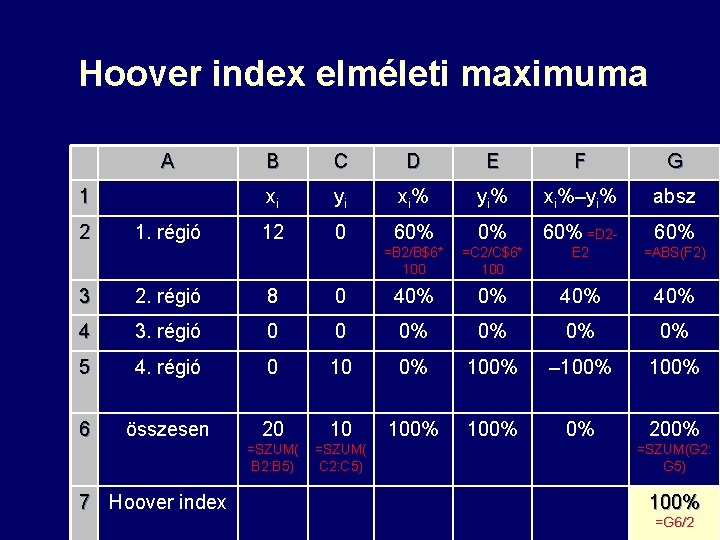
Hoover index elméleti maximuma A 1 2 1. régió B C D E F G xi yi xi% yi% xi%–yi% absz 12 0 60% 0% 60% =D 2 - 60% =B 2/B$6* 100 =C 2/C$6* 100 E 2 =ABS(F 2) 3 2. régió 8 0 40% 0% 40% 4 3. régió 0 0 0% 0% 5 4. régió 0 10 0% 100% – 100% 6 összesen 20 10 100% 0% 200% =SZUM( B 2: B 5) =SZUM( C 2: C 5) 7 Hoover index =SZUM(G 2: G 5) 27 100% =G 6/2
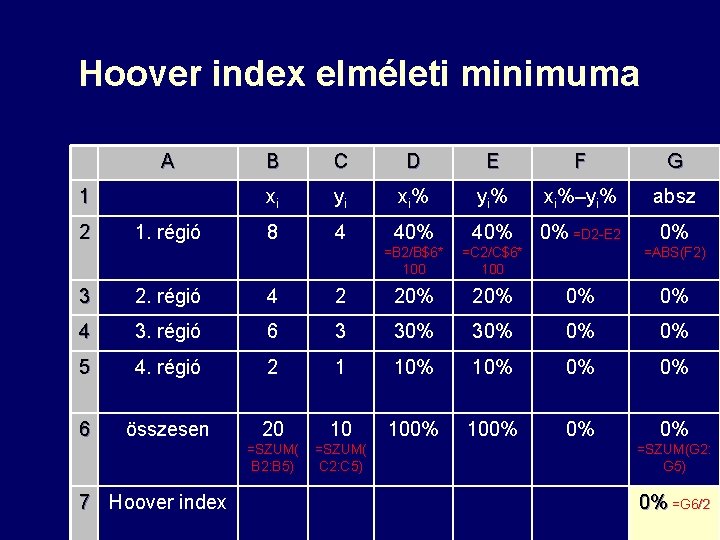
Hoover index elméleti minimuma A 1 2 1. régió B C D E F G xi yi xi% yi% xi%–yi% absz 8 4 40% 0% =D 2 -E 2 0% =B 2/B$6* 100 =C 2/C$6* 100 =ABS(F 2) 3 2. régió 4 2 20% 0% 0% 4 3. régió 6 3 30% 0% 0% 5 4. régió 2 1 10% 0% 0% 6 összesen 20 10 100% 0% 0% =SZUM( B 2: B 5) =SZUM( C 2: C 5) 7 Hoover index =SZUM(G 2: G 5) 0%28 =G 6/2

„Pszeudo-egymutatós” egyenlőtlenségi index n Két nem fajlagos mutató területi eloszlása közötti eltérés mérése – Pl. nép-jöv, kisebbség-egész társadalom stb. n Egy fajlagos mutató területi egyenlőtlenségének mérése – Pl. Jöv/fő, kisebbségek aránya 29

Hoover index használhatósága n Egyik legjobban interpretálható eredményt adja a területi egyenlőtlenségi indexek közül – Értékei 0– 100 között mozognak: a 100 magas, a 0 alacsony érték (szórás-típusú területi egyenlőtlenségi mutatóknak nincs maximuma) – H = 33% az egyik mutató 33 %-át kell a régiók között átcsoportosítani ahhoz, hogy a területi megoszlása megegyezzen a másikéval 30

Hoover index más neveken n Robin Hood index („Rózsa Sándor” index) – Népesség és jövedelem között n Dinamikus értelmezés (itt lehet az egy évre jutó változást is mérni, ha 2 helyett 2 t-vel osztunk) – Korábbi és későbbi állapotok között n (Településszociológiában Duncan&Duncan házaspár) – Disszimilaritási index: rész–rész viszonylatban – Szegregációs index: rész–egész viszonylatban, vagy rész–többi rész viszonylatban n n Egyes változatoknál nem százalékban fejezzük ki, ekkor értékkészlete: 0 ≤ H ≤ 1 Krugman index (Földrajz és kereskedelem c. könyv, 1993. ) – – Ha nem osztjuk el 2 -vel (nehezebben értelmezhető) 0 ≤ H ≤ 200 (vagy 0 ≤ H ≤ 2) 31

Hoover index vizsgálati lehetőségei n n Magyarország 2005 jöv-nép megyei szint Egy számítás önmagában általában kevés összehasonlítás kell: – Területek között: pl. Szlovákiára is – Időbeni állapotok között: pl. 1990 -re is – Mutatók között: pl. személygépkocsi és a népesség között is – Területi szinteken (Hoover-index specialitása): pl. települési szinten is 32
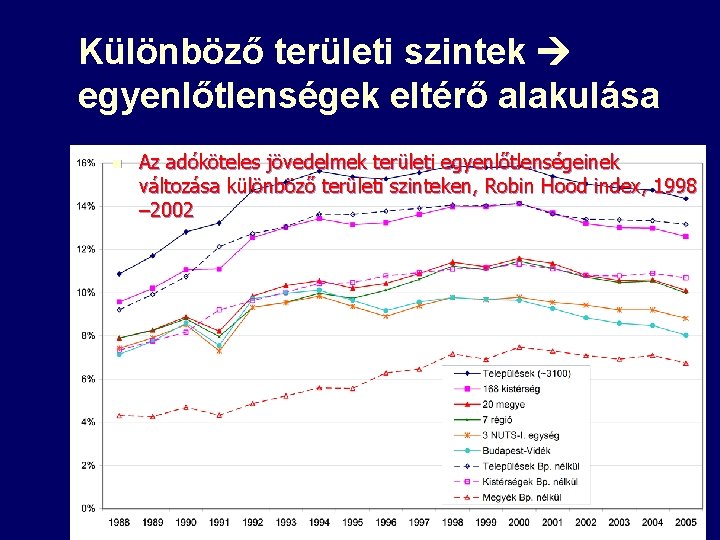
Különböző területi szintek egyenlőtlenségek eltérő alakulása n Az adóköteles jövedelmek területi egyenlőtlenségeinek változása különböző területi szinteken, Robin Hood index, 1998 – 2002 33
- Slides: 33