TeoriBahasadanOtomata Lecture 6 Non Deterministik FINITE STATE AUTOMATA

Teori-Bahasa-dan-Otomata Lecture #6 Non Deterministik FINITE STATE AUTOMATA

Reduksi Jumlah State Pada FSA • Reduksi dilakukan untuk mengurangi jumlah state tanpa mengurangi kemampuan untuk menerima suatu bahasa seperti semula (efisiensi) • State pada FSA dapat direduksi apabila terdapat useless state • Hasil dari FSA yang direduksi merupakan ekivalensi dari FSA semula

Reduksi Jumlah State Pada FSA Pasangan State dapat dikelompokkan berdasarkan: • Distinguishable State (dapat dibedakan) Dua state p dan q dari suatu DFA dikatakan indistinguishable apabila: δ(q, w) F dan δ(p, w) F atau δ(q, w) ∉ F dan δ(p, w) ∉ F untuk semua w S* • Indistinguishable State ( tidak dapat dibedakan) Dua state p dan q dari suatu DFA dikatakan distinguishable jika ada string w S* hingga: δ(q, w) F dan δ(p, w) ∉ F

Reduksi Jumlah State Pada FSA - Relasi Pasangan dua buah state memiliki salah satu kemungkinan : distinguishable atau indistinguishable tetapi tidak kedua-duanya. Dalam hal ini terdapat sebuah relasi : Jika dan maka p, r p dan q indistinguishable, q dan r indistinguishable dan p, q, r indistinguishable Dalam melakukan eveluasi state, didefinisikan suatu relasi : Untuk Q yg merupakan himpunan semua state – D adalah himpunan state-state distinguishable, dimana D Q – N adalah himpunan state-state indistinguishable, dimana N Q – maka x N jika x Q dan x D

Reduksi Jumlah State Pada FSA – Step Hapuslah semua state yg tidak dapat dicapai dari state awal (useless state) Buatlah semua pasangan state (p, q) yang distinguishable, dimana p F dan q F. Catat semua pasangan-pasangan state tersebut. • Cari state lain yang distinguishable dengan aturan: “Untuk semua (p, q) dan semua a ∑, hitunglah δ (p, a) = pa dan δ (q, a) = qa . Jika pasangan (pa, qa) adalah pasangan state yang distinguishable maka pasangan (p, q) juga termasuk pasangan yang distinguishable. • Semua pasangan state yang tidak termasuk sebagai state yang distinguishable merupakanstate-state indistinguishable. • Beberapa state yang indistinguishable dapat digabungkan menjadi satu state. • Sesuaikan transisi dari state-state gabungan tersebut. • •
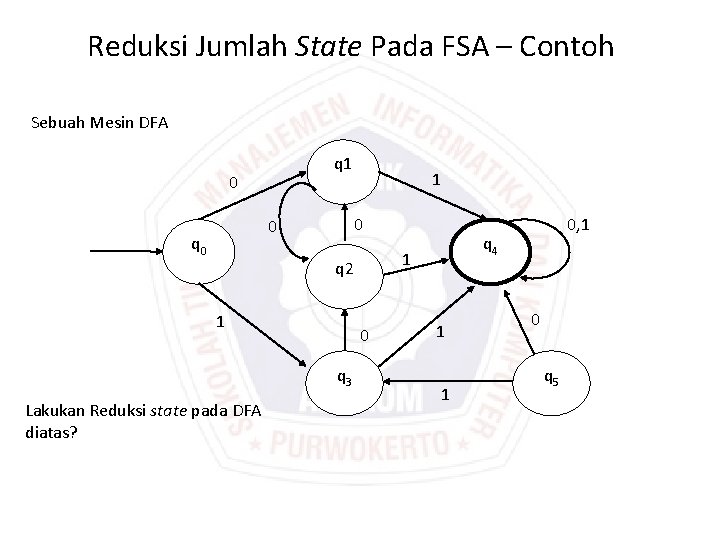
Reduksi Jumlah State Pada FSA – Contoh Sebuah Mesin DFA q 1 0 0 0 q 0 1 1 0 q 3 Lakukan Reduksi state pada DFA diatas? q 4 1 q 2 0, 1 1 1 0 q 5

Reduksi Jumlah State Pada FSA – Step • State q 5 tidak dapat dicapai dari state awal dengan jalan apapun (useless state). Hapus state q 5 • Catat state-state distinguishable, yaitu : q 4 F sedang q 0, q 1, q 2, q 3 F sehingga pasangan (q 0, q 4) (q 1, q 4) (q 2, q 4) dan (q 3, q 4) adalah distinguishable. • Pasangan-pasangan state lain yang distinguishable diturunkan berdasarkan pasangan dari langkah 2, yaitu : – Untuk pasangan (q 0, q 1) δ(q 0, 0) = q 1 dan δ(q 1, 0) = q 2 belum teridentifikasi δ(q 0, 1) = q 3 dan δ(q 1, 1) = q 4 (q 3, q 4) distinguishable maka (q 0, q 1) adalah distinguishable. – Untuk pasangan (q 0, q 2) δ(q 0, 0) = q 1 dan δ(q 2, 0) = q 1 belum teridentifikasi δ(q 0, 1) = q 3 dan δ(q 2, 1) = q 4 (q 3, q 4) distinguishable maka (q 0, q 2) adalah distinguishable.
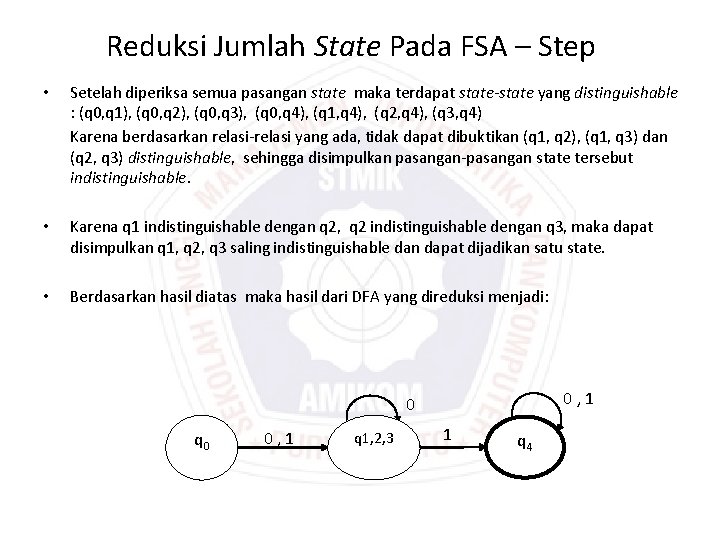
Reduksi Jumlah State Pada FSA – Step • Setelah diperiksa semua pasangan state maka terdapat state-state yang distinguishable : (q 0, q 1), (q 0, q 2), (q 0, q 3), (q 0, q 4), (q 1, q 4), (q 2, q 4), (q 3, q 4) Karena berdasarkan relasi-relasi yang ada, tidak dapat dibuktikan (q 1, q 2), (q 1, q 3) dan (q 2, q 3) distinguishable, sehingga disimpulkan pasangan-pasangan state tersebut indistinguishable. • Karena q 1 indistinguishable dengan q 2, q 2 indistinguishable dengan q 3, maka dapat disimpulkan q 1, q 2, q 3 saling indistinguishable dan dapat dijadikan satu state. • Berdasarkan hasil diatas maka hasil dari DFA yang direduksi menjadi: 0 , 1 0 q 0 0 , 1 q 1, 2, 3 1 q 4

Non Deterministic Finite Automata Non Deterministic finite automata (NFA) M = (Q, ∑, δ, S, F), dimana : Q : himpunan state/kedudukan ∑ : himpunan simbol input ∂ : fungsi transisi, dimana ∂ Q x (∑ ⋃ ) P(Q) : set of all subsets of Q S : State awal (initial state) F : himpunan state akhir (Final State) Language L(M) : (x| ∂(S, x) di dalam F)

Non Deterministic Finite Automata Berikut ini sebuah contoh NFA (Q, ∑, δ, S, F). dimana : Q = {q 0, q 1 , q 2 , q 3 , q 4 } δ diberikan dalam tabel berikut : δ a b c S = q 0 Q 0 {q 0 , q 1} {q 0 , q 2 } {q 0 , q 3 } F = {q 4} q 1 {q 1 , q 4 } {q 1} q 2 {q 2 } {q 2, q 4 } {q 2} q 3 {q 3 } {q 3, q 4 } q 4 ∑= {a, b, c}
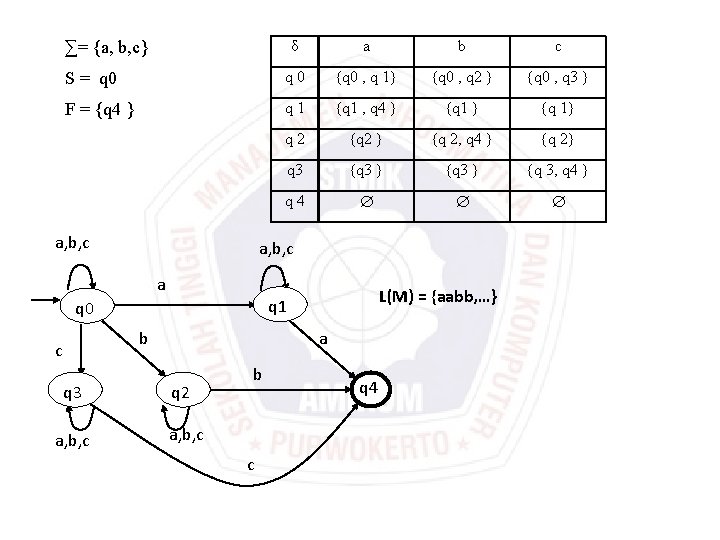
δ a b c S = q 0 {q 0 , q 1} {q 0 , q 2 } {q 0 , q 3 } F = {q 4 } q 1 {q 1 , q 4 } {q 1} q 2 {q 2 } {q 2, q 4 } {q 2} q 3 {q 3 } {q 3, q 4 } q 4 ∑= {a, b, c} a, b, c a b c q 3 a, b, c L(M) = {aabb, …} q 1 q 0 a q 2 b a, b, c c q 4

Sebuah kalimat di terima NFA jika : Salah satu tracing-nya berakhir di state AKHIR, atau himpunan state setelah membaca string tersebut mengandung state AKHIR Telusurilah, apakah kalimat-kalimat berikut diterima NFA di atas : ab, abc, aabb Jawab: δ(q 0 , ab) δ(q 0, b) δ(q 1 , b) {q 0, q 2} {q 1 } = {q 0 , q 1 , q 2} Himpunan state TIDAK mengandung state AKHIR kalimat ab tidak diterima δ(q 0 , abc) δ(q 0 , bc) δ(q 1 , bc) { δ(q 0 , c) δ(q 2 , c)} δ(q 1 , c) {{ q 0 , q 3 } { q 2 }} { q 1 } = {q 0 , q 1 , q 2 , q 3 } Himpunan state TIDAK mengandung state AKHIR kalimat abc tidak diterima
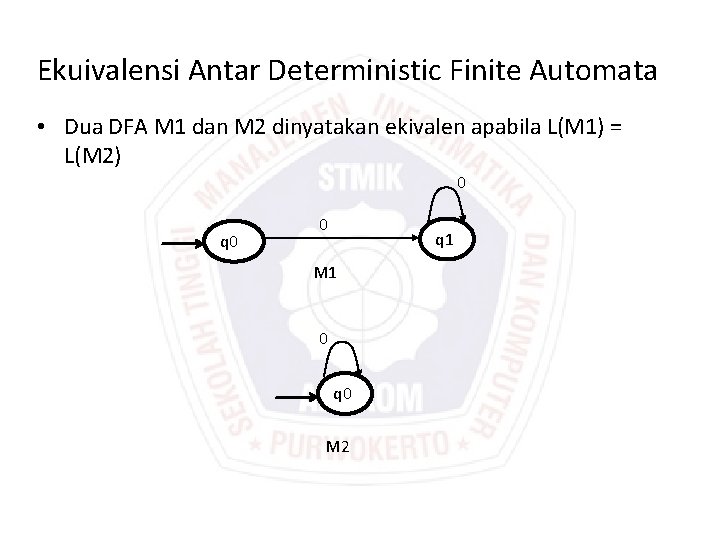
Ekuivalensi Antar Deterministic Finite Automata • Dua DFA M 1 dan M 2 dinyatakan ekivalen apabila L(M 1) = L(M 2) 0 q 0 0 q 1 M 1 0 q 0 M 2

Non Deterministic Finite Automata dengan ε-move • NFA dengan ε-move (transisi ε), diperbolehkan merubah state tanpa membaca input. • Disebut dengan ε-move karena tidak bergantung pada suatu input ketika melakukan transisi. • Kegunaan ε-move adalah untuk memudahkan mengkombinasikan finite state automata. • ε-closure (q 0)=himpunan state-state yang dapat dicapai dari state q 0 tanpa membaca input. • Pada suatu state yang tidak memiliki ε-move, maka ε-closure nya adalah state itu sendiri. • ε-closure adalah himpunan state-state yang dapat dicapai dari suatu state tanpa membaca input.
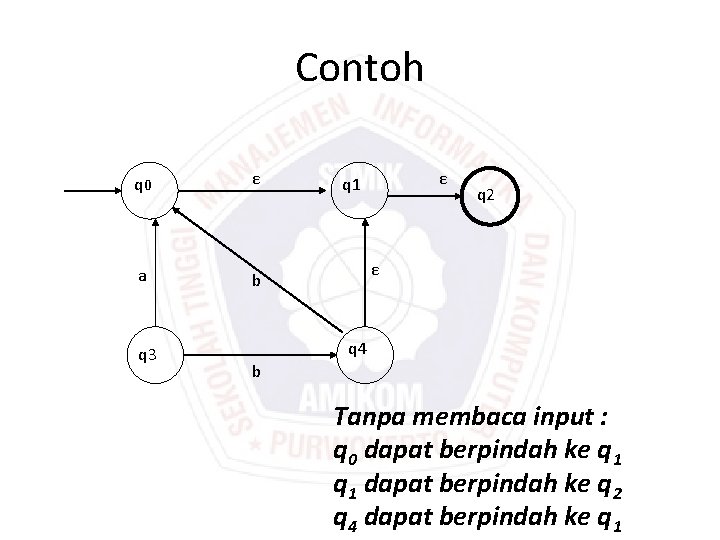
Contoh q 0 ε a b q 3 ε q 1 q 2 ε q 4 b Tanpa membaca input : q 0 dapat berpindah ke q 1 dapat berpindah ke q 2 q 4 dapat berpindah ke q 1

ε-closure(q 0) = {q 0, q 1, q 2 }, artinya dari state q 0 tanpa membaca input dapat mencapai state q 0, q 1 dan q 2. ε-closure untuk state lainnya : ε-closure(q 1) = {q 1, q 2 } ε-closure(q 2) = {q 2 } ε-closure(q 3) = {q 3 } ε-closure(q 4) = {q 4 }
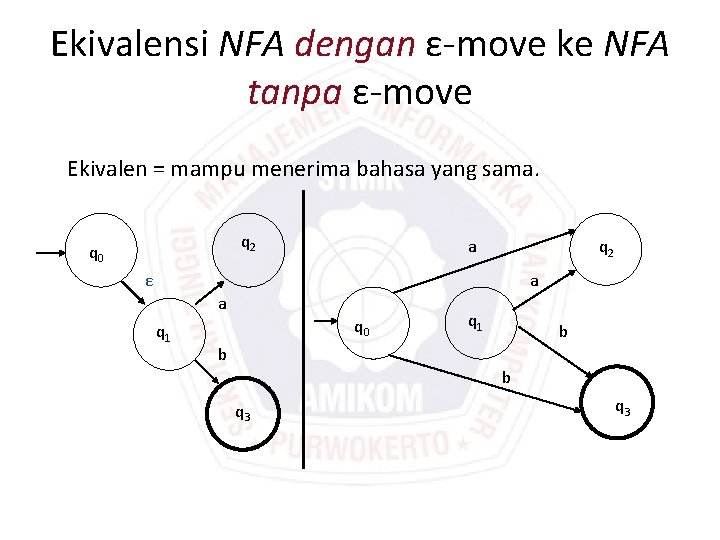
Ekivalensi NFA dengan ε-move ke NFA tanpa ε-move Ekivalen = mampu menerima bahasa yang sama. q 2 q 0 a q 2 ε a a q 1 q 0 q 1 b b b q 3

Merubah NFA dengan ε-move ke NFA tanpa ε-move. • Buat tabel transisi NFA ε-move dari diagram NFA atau sudah ditentukan semula. • Carilah ε-closure untuk setiap state NFA. • Cari setiap fungsi transisi hasil perubahan dari NFA ε-move ke NFA tanpa ε-move (δ) , rumus : ’(state, input)= -closure( ( -closure(state, input))

• Berdasarkan langkah sebelumnya, buatlah tabel transisi NFA yg baru tanpa ε-move • Tentukan state akhir. Jika State 2 x pada closure satu state merup final state maka state yg baru menjadi finel state. F’ = F {q | ( -closure(q) F }
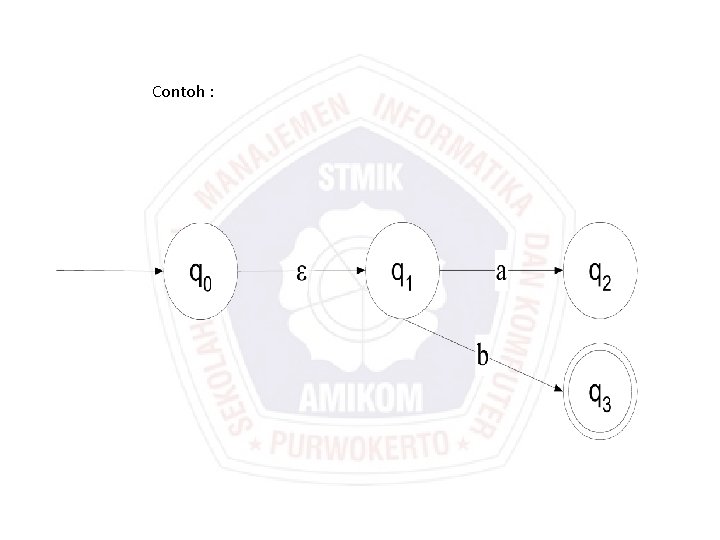
Contoh :
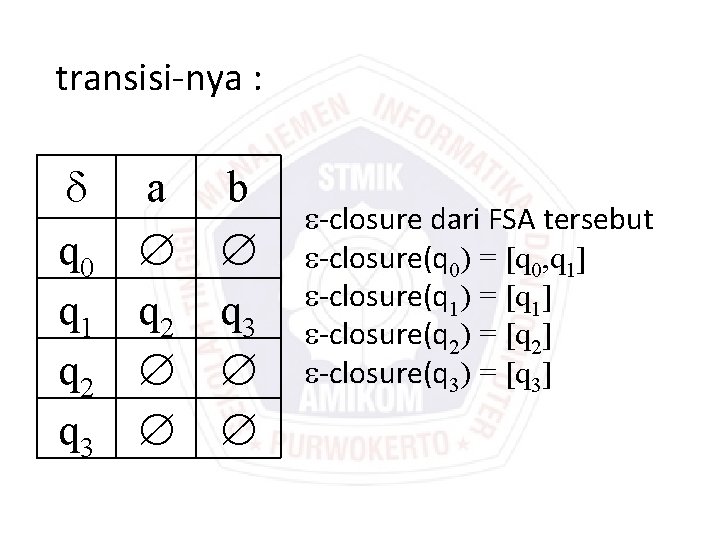
transisi-nya : q 0 q 1 q 2 q 3 a q 2 b q 3 -closure dari FSA tersebut -closure(q 0) = [q 0, q 1] -closure(q 1) = [q 1] -closure(q 2) = [q 2] -closure(q 3) = [q 3]
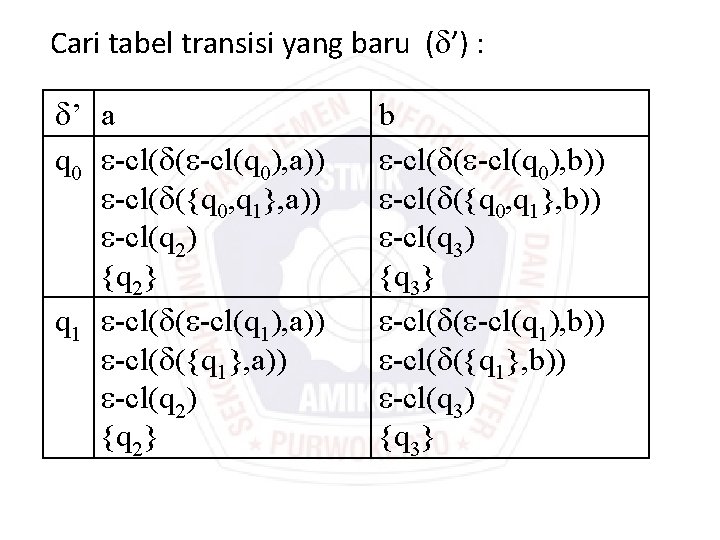
Cari tabel transisi yang baru ( ’) : ’ a q 0 -cl( ( -cl(q 0), a)) -cl( ({q 0, q 1}, a)) -cl(q 2) {q 2} q 1 -cl( ( -cl(q 1), a)) -cl( ({q 1}, a)) -cl(q 2) {q 2} b -cl( ( -cl(q 0), b)) -cl( ({q 0, q 1}, b)) -cl(q 3) {q 3} -cl( ( -cl(q 1), b)) -cl( ({q 1}, b)) -cl(q 3) {q 3}
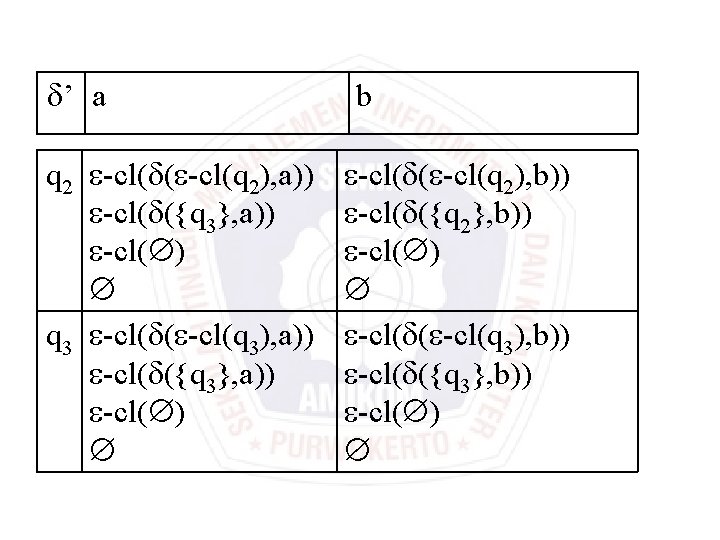
’ a q 2 -cl( ( -cl(q 2), a)) -cl( ({q 3}, a)) -cl( ) q 3 -cl( ( -cl(q 3), a)) -cl( ({q 3}, a)) -cl( ) b -cl( ( -cl(q 2), b)) -cl( ({q 2}, b)) -cl( ) -cl( ( -cl(q 3), b)) -cl( ({q 3}, b)) -cl( )
- Slides: 23