TEORI PROBABILITAS DISTRIBUSI PELUANG KONTINU UNIFORM GAMMA DAN

TEORI PROBABILITAS DISTRIBUSI PELUANG KONTINU (UNIFORM, GAMMA, DAN EKSPONENSIAL) DESTYANTO ANGGORO 1

DEFINISI Dalam ilmu statistika matematika, teori peluang (probability theory) merupakan dasar dan pengantar untuk penyusunan statistika lebih jauh, dimana dipakai pada penentuan selang untuk distribusi peluang yang terbagi atas distribusi peluang diskrit dan distribusi peluang kontinu (Bain 1991). 2

Macam Distribusi Probabilitas • Distribusi Probabilitas Variabel Diskrit: �Distribusi Binomial �Disribusi Hipergeometrik �Distribusi Poisson • Distribusi Probabilitas Variabel Kontinu: �Distribusi Uniform �Distribusi Gamma �Distribusi Eksponensial �Distribusi Weibull �Distribusi Normal �Distribusi Chi Square 3

Distribusi Uniform • Merupakan jenis distribusi variabel acak kontinyu • Pada distribusi ini setiap variabel acak yang muncul memiliki probabilitas yang sama, dimana: 1 f x | k ; untuk x 1, x 2, . . . , x k k • Jika nilai dari variabel acak tersebut tersebar pada sebuah interval (a, b), maka pdf dari distribusi uniform dinyatakan sebagai: f x | a, b 1 ; a x b b a 4

Distribusi Uniform • Mean dari distribusi uniform: E X a b 2 • Varians dari distribusi uniform: 2 b a 2 12 • Fungsi Distribusi Kumulatif (cdf) dari distribusi uniform dinyatakan sebagai: x a 0; x a F x ; a x b b a x b 1; 5

Contoh kasus: Jika waktu seseorang menunggu datangnya pesawat disebuah bandara antara jam 08. 00 -10. 00 berdistribusi uniform. Hitung berapa probabilitas seseorang harus menunggu a. Kurang atau sama dengan 30 menit dari jam 08. 00? b. Lebih dari 30 Menit Jawab: a. Waktu 08. 00 – 10. 00 adalah 120 menit, maka P X 30 b. . 120 1 120 0 dx 0, 25 0 P X 30 1 P X 30 = 1 0, 25 = 0, 75 6

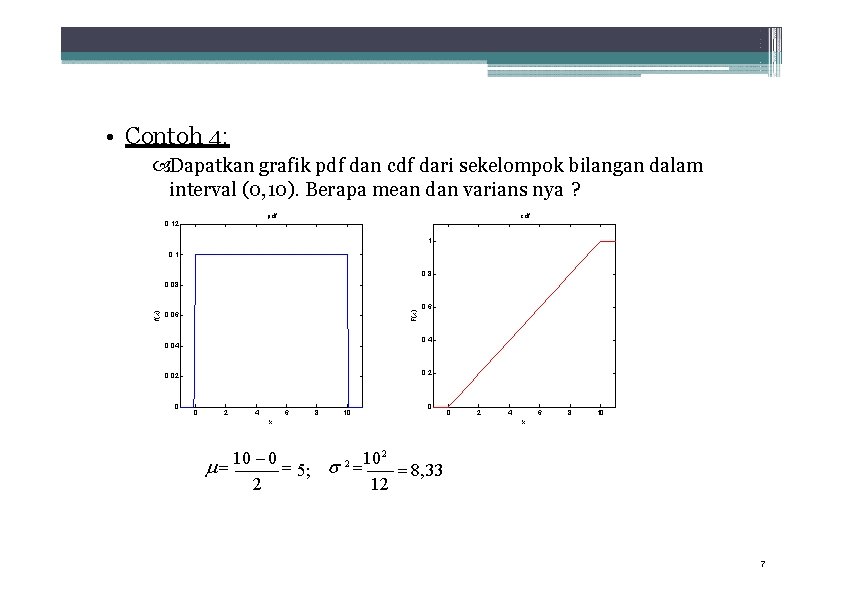
• Contoh 4: Dapatkan grafik pdf dan cdf dari sekelompok bilangan dalam interval (0, 10). Berapa mean dan varians nya ? pdf cdf 0. 12 1 0. 8 F(x) f(x) 0. 08 0. 06 0. 4 0. 04 0. 2 0. 02 0 0. 6 0 2 4 6 8 10 0 x 0 2 4 6 8 10 x 2 10 0 2 10 5; 8, 33 2 12 7

Distribusi Gamma dan Eksponensial • Digunakan untuk memodelkan jumlahan waktu hingga kemunculan sebuah event tertentu, atau memodelkan waktu di antara event-event yang saling independen • Beberapa aplikasi distribusi eksponensial contohnya pemodelan waktu hingga komputer log off, pemodelan waktu antara waktu kedatangan panggilan telepon, dan pemodelan waktu lainnya. 8

Distribusi Gamma dan Eksponensial • Fungsi kerapatan probabilitas (pdf) eksponensial, dinyatakan sebagai sbb: e x ; f x | 0; dari distribusi x 0; 0 x lainnya • Mean dari distribusi variabel acak eksponensial dinyatakan sebagai: E X 1 • variance sbb: V X 2 1 2 9

Distribusi Gamma dan Eksponensial • Fungsi Distribusi Kumulatif (cdf) dari distribusi eksponensial dinyatakan sebagai berikut: x 0 0; F x x 1 e ; x 0 • Jika distribusi eksponensial digunakan untuk merepresentasikan waktu antar kedatangan (inter arrival time), maka parameter adalah sebuah kecepatan dengan satuan kedatangan periode waktu. 10

• Contoh Kasus: Waktu kedatangan busway pada sebuah halte interseksi mengikuti distribusi eksponensial dengan mean 12 detik. Berapa probabilitas dimana waktu antar kedatangan adalah 10 detik atau kurang ? Gambarkan grafik pdf dan cdf –nya. Jawab: Rata-rata interarrival time (waktu kedatangan)=12, jadi 1 12 Sehingga: P X 10 1 e 1/12 10 0, 57 pdf distribusi eksponensial P(X<10) cdf distribusi eksponensial P(X<10) 12 1 =1/12 0. 9 10 0. 8 0. 7 8 6 F(x) f(x) 0. 6 0. 5 0. 4 4 0. 3 0. 2 2 0. 1 0 0 1 2 3 4 5 x 6 7 8 9 10 11

Distribusi Gamma • Mean dari distribusi probabilitas gamma: E X t • Variance dari distribusi probabilitas gamma: V X t 2 • Fungsi distribusi kumulatif (cdf) dari distribusi gamma: 0; x 0 F x; , t 1 x t 1 y t y e dy; 0 x 0 12

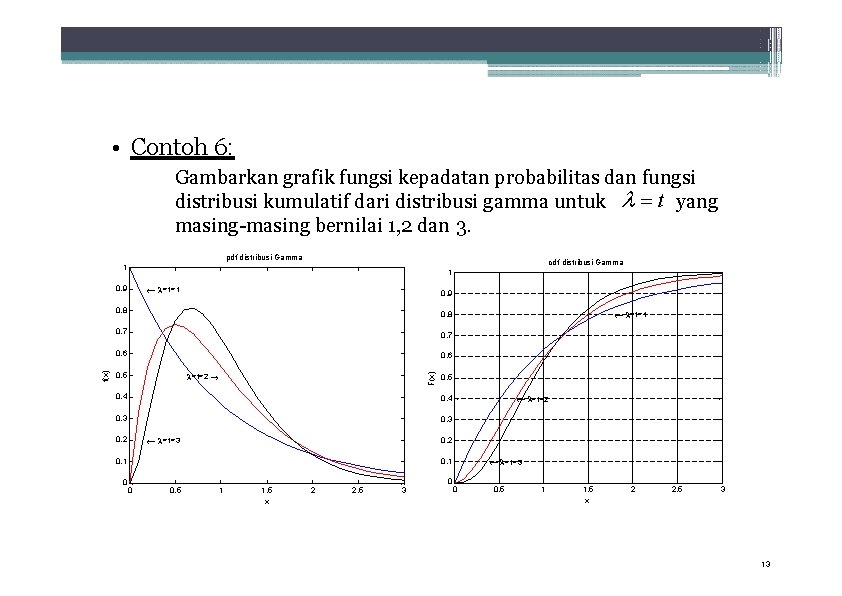
• Contoh 6: Gambarkan grafik fungsi kepadatan probabilitas dan fungsi distribusi kumulatif dari distribusi gamma untuk t yang masing-masing bernilai 1, 2 dan 3. pdf distribusi Gamma cdf distribusi Gamma 1 1 =t=1 0. 9 0. 8 0. 7 0. 6 0. 5 =t=2 F(x) f(x) 0. 9 0. 5 0. 4 0. 3 0. 2 =t=3 =t=2 0. 1 0 =t=1 0 0. 5 1 1. 5 x 2 2. 5 3 0 =t=3 0 0. 5 1 1. 5 x 2 2. 5 3 13

Contoh Kasus Proses poisson dapat diterapkan dengan menunggu 3 kejadian poisson terjadi mempunyai distibusi gamma dengan ẞ = 1/6 dan α = 3. Misalkan X adalah selang waktu sebelum 3 panggilan telepon datang. Probabilitasnya adalah : P ( X ≤ x) = = 14