TEORI PERMINTAAN PENDAHULUAN PENDEKATAN UTILITAS KARDINAL Utilitas Marginal

TEORI PERMINTAAN PENDAHULUAN PENDEKATAN UTILITAS KARDINAL - Utilitas - Marginal Utilitas - Kondisi Keseimbangan Konsumen konsumsi satu jenis barang menurunkan fungsi permintaan Konsumsi lebih dari satu barang PENDEKATAN UTILITAS ORDINAL - Kurva Indeveren - Marginal Rates Substitutions (MRS) - Budget Line - Keseimbangan Konsumen - Derivasi Teori Permintaan - Substitution effect dan Income Effect FUNGSI PERMINTAAN, FUNGSI REVENUE dan ELASTISITAS PERMINTAAN by L 2 A 164 1

PENDAHULUAN Teori Permintaan pada dasarnya membahas Teori Perilaku Konsumen dalam mengkonsumsi barang. D x = f (Px, I, Py)) Hukum Permintaan. Salah satu aspek dari Hukum atau Teori Permintaan adalah “hubungan antara Dx dan Px bersifat negatif. ” P P↓ X ↑ P↑ X ↓ X Hubungan semacam ini akan kita buktikan dengan beberapa pendekatan. by L 2 A 164 2

PENDEKATAN UTILITAS KARDINAL Utilitas (TU) - Utilitas (utility = Dayaguna atau kepuasan yang diperoleh konsumen dari penggunaan barang / jasa (misalnya X). - Asumsi : utilitas dapat diukur secara kardinal atau bahkan dapat dinilai dengan uang - X ↑ Utilitas TU ↑, dengan ∆TU ↓ sehingga TU max Marginal (MU) Kalau konsumen terus menambah konsumsi X, - ∆X TU ↓ ∆TU - Pertanyaan : Berapakah ∆TU jika ∆X hanya satu unit saja ? ∆TU dikarenakan ∆X satu unit inilah yang disebut sebagai “Marginal Utilitas” by L 2 A 164 3

Gambaran pengukuran TU dan MU dapat dicontohkan sebagai berikut : ΔX = 3 unit X = 2 TU = 10 ΔTU = 15 X = 5 TU =util 25 ΔX = 3 unit ΔTU = 15 ΔX = 1 unit ΔTU = 15 / 3 = 5 – X = U T 2 X 16 MU=1 6 – 2 X by L 2 A 164 4

X 0 2 4 6 8 10 TU 0 28 48 60 64 60 MU =ΔTU / ΔX 14 10 6 2 -2 MU = d. TU/d. X 16 12 8 4 0 -4 MU = f(X) MU = d. TU/d. X = 16 – TU = 16 X – 2 2 X adalah sejumlah brg yg - Yang. Xdimaksud permintaan akan dibeli kosumen sehingga kepuasannya maksimum Maximize kepuasan (TU) sebagai tujuan. - tujuan tsb tercapai harus memenuhi syarat / kond. Agar isi keseimbangan : MU = 0 16 – 2 X = 0 X = 8 (permintaan 5 TU = f(X)

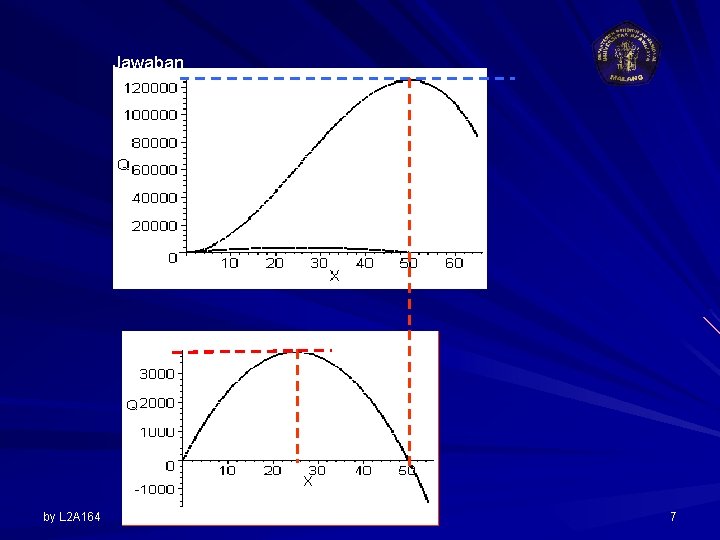
Contoh Kepuasan seorang konsumen atas suatu produk yang dikonsumsi adalah TU = 100 + 150 Q 2 – 2 Q 3 a) Tentukan ekspresi dari marginal utility b) Gambarkan fungsi TU dan MU c) Berapakah besarnya TU dan MU jika Q = 5 unit d) Berapa Q harus dikonsumsi sehingga TU max e) Berapa konsumsi Q pada MU mulai by L 2 A 164 6

Jawaban by L 2 A 164 7

MENURUNKAN FUNGSI / KURVA PERMINTAAN (Dx = f(Px) - Realitanya seorang konsumen dalam membeli barang (X) akan berhadapan dengan harganya (Px) Analisis hubungan antara harga dan permintaan barang. - Untuk memperoleh sejumlah barang diperlukan pengeluaran atau biaya (Z), yang dapat dihitung : -Z Dengan = Px. demikian, X ( Z sekarang = f(X) ) tujuan konsumen tidak semata-mata memaksisimumkan TU saja, tetapi harus memperhitungkan biayanya, yang berarti konsumen harus memaksimumkan selisih (S) antara TU dan Z (S = TU – Z), yaitu : by L 2 A 164 8

Maximize : S = TU - Z = f (X) Px. X Agar S maksimum , maka : Jika Px = 6, maka : X = 8 – 0, 5 Px X = 8 - 0, 5(6) = 5 TU = 16(5) – 52 = 55 Z = 6(X) = 30 S = TU – Z = 25 Dari contoh di atas, maka hukum permintaan terbukti : MUx = Px 16 – 2 X = Px X = 8 – 0, 5 Px ↓ X↑ by L 2 A 164 9

KONDISI KESEIMBANGAN KONSUMEN DENGAN KONSUMSI LEBIH DARI SATU BARANG - Untuk kondisi yang lebih nyata lagi, perilaku konsumen menghadapi berbagai pilihan barang dan terbatasnya dana yang dimiliki, TU = f (X 1, menghadapi X 2, . . Xn) harganya disamping C = Px 1 X 1 + Px 2 X 2. . + Pxn. Xn L = f (X 1, X 2, . . Xn) + ( ג C – Px 1 X 1 – Px 2 X 2. . – Pxn. Xn ) (Kondisi keseimbangan konsumen) by L 2 A 164

Contoh : Seorang konsumen diperkirakan mempunyai fungsi utilitas atas barang X dan Y seperti : TU = 10 X + 24 Y – 0, 5 X 2 – 0, 5 Y 2. Harga X (Px) = $2 dan harga Y (Py) = $6. Sedangkan dana yang dimilki sebesr $44. Pertanyaan : Berapa banyak barang X dan Y harus dibeli konsumen agar kepuasannya maksimum ? by L 2 A 164 11

Penyelesaian : Maksimumkan : TU = 10 X + 24 Y – 0, 5 X 2 – 0, 5 Y 2 Kendala : 44 = 2 X + 6 Y 44 = 2 X + 6(3 X 6) 44 = 20 X – 36 X = 4 Y = 3(4) – 6 = 6 by L 2 A 164 44 = 2 X + 6 Y 44 = 2(2 +⅓Y)+6 Y 44 = 4+⅔Y+6 Y 40 = 6⅔Y→Y=6 dan X=4 12

TU = 10(4) + 24(6) – 0, 5(42) – 0, 5(62) = 158 ( = ג 10 – 4)/2 = (24 – 6)/6 = 3 Jadi pembelian barang X = 4 unit dan Y = 6 unit, dan total kepuasannya sebanyak 158 utils. = ג 3 mengartikan pengaruh perubahan per $ terhadap fungsi TU (kepuasan), sebesar + 3 kali. Jadi kalau dana ditambah $10, maka TU akan bertambah sebesar +30 utils (3 x 10). Coba buktikan ! by L 2 A 164 13

Latihan : Tentukan kombinasi konsumsi barang X dan Y, sehingga kepuasan maksimum, jika : (a) TU = 12 X Y Px = $3, Py = $6 dan Dana = $60 (b) TU = 17 X + 20 Y – 2 X 2 – Y 2 Px = $3, Py = $6 dan Dana = $60 2 (c) TU = 18 X – X dan harga barang = Rp 8, -. Maka hitunglah : permintaan barang. by L 2 A 164 14

1. a) Apa yang dimaksud dengan permintaanabsulut dan permintaan efektive b) Jelaskan dengan singkat mengapa teor biaya dan teori renvenue bisa diturunkan dari teori produksi. 2. j. Ika diketahui TU = 18 X – X 2 dan harga barang = Rp 8, -. Maka hitunglah permintaan barang. 3. Tentukan kombinasi konsumsi barang X dan Y, sehingga kepuasan maksimum, jika : (a) TU = 12 X Y; Px = $3, Py = $6 dan Dana = $60 (b) TU = 17 X + 20 Y – 2 X 2 – Y 2 Px = $3, Py = $6 dan Dana = $60 by L 2 A 164 15