TEORI PERMINTAAN PENDAHULUAN PENDEKATAN UTILITAS KARDINAL Utilitas Marginal

TEORI PERMINTAAN PENDAHULUAN PENDEKATAN UTILITAS KARDINAL - Utilitas - Marginal Utilitas - Kondisi Keseimbangan Konsumen konsumsi satu jenis barang menurunkan fungsi permintaan Konsumsi lebih dari satu barang PENDEKATAN UTILITAS ORDINAL - Kurva Indeveren - Marginal Rates Substitutions (MRS) - Budget Line - Keseimbangan Konsumen - Derivasi Teori Permintaan - Substitution effect dan Income Effect FUNGSI PERMINTAAN, FUNGSI REVENUE dan ELASTISITAS PERMINTAAN by L 2 A 164 1

PENDAHULUAN Teori Permintaan pada dasarnya membahas Teori Perilaku Konsumen dalam mengkonsumsi barang. D x = f (Px, I, Py)) Hukum Permintaan. Salah satu aspek dari Hukum atau Teori Permintaan adalah “hubungan antara Dx dan Px bersifat negatif. ” P P↓ X ↑ P↑ X ↓ X Hubungan semacam ini akan kita buktikan dengan beberapa pendekatan. by L 2 A 164 2

PENDEKATAN UTILITAS KARDINAL Utilitas (TU) - Utilitas (utility = Dayaguna atau kepuasan yang diperoleh konsumen dari penggunaan barang / jasa (misalnya X). - Asumsi : utilitas dapat diukur secara kardinal atau bahkan dapat dinilai dengan uang - XMarginal ↑ TUUtilitas ↑, dengan ∆TU ↓ sehingga TU max (MU) Kalau konsumen terus menambah konsumsi X, - ∆X TU ↓ ∆TU - Pertanyaan : Berapakah ∆TU jika ∆X hanya satu unit saja ? ∆TU dikarenakan ∆X satu unit inilah yang disebut sebagai “Marginal Utilitas” by L 2 A 164 3

Gambaran pengukuran TU dan MU dapat dicontohkan sebagai berikut : ΔX = 3 unit X = 2 TU = 10 ΔTU = 15 X = 5 TU =util 25 ΔX = 3 unit ΔTU = 15 ΔX = 1 unit ΔTU = 15 / 3 = 5 – X 16 = U T 2 X MU=1 6 – 2 X by L 2 A 164 4

X 0 2 4 6 8 10 TU 0 28 48 60 64 60 MU =ΔTU / ΔX 14 10 6 2 -2 MU = d. TU/d. X 16 12 8 4 0 -4 TU = f(X) MU = f(X) TU = 16 X – MU = d. TU/d. X = 16 – 2 2 X adalah sejumlah brg yg - Yang. Xdimaksud permintaan akan dibeli kosumen sehingga kepuasannya maksimum Maximize kepuasan (TU) sebagai tujuan. - Agar tujuan tsb tercapai harus memenuhi syarat / kondisi keseimbangan : MU = 0 16 – 2 X = 0 X = 8 (permintaan 5

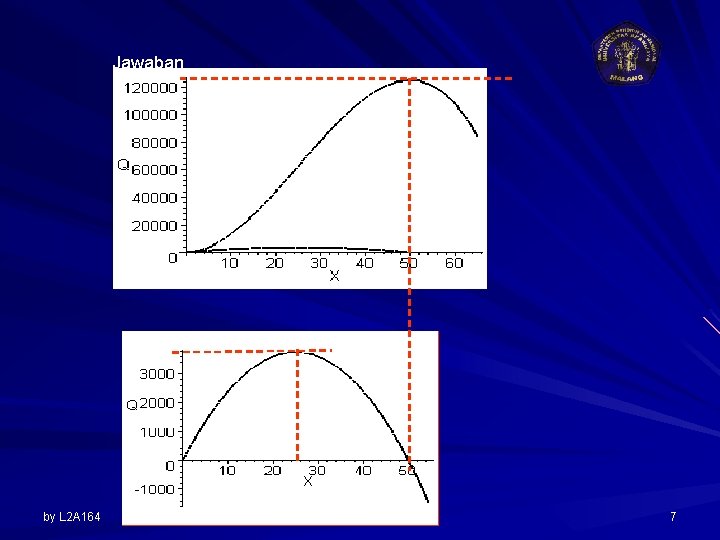
Contoh Kepuasan seorang konsumen atas suatu produk yang dikonsumsi adalah TU = 100 + 150 Q 2 – 2 Q 3 a) Tentukan ekspresi dari marginal utility b) Gambarkan fungsi TU dan MU c) Berapakah besarnya TU dan MU jika Q = 5 unit ? d) Berapa Q harus dikonsumsi sehingga TU max e) Berapa konsumsi Q pada MU mulai menurun. by L 2 A 164 6

Jawaban by L 2 A 164 7

MENURUNKAN FUNGSI / KURVA PERMINTAAN (Dx = f(Px) - Realitanya seorang konsumen dalam membeli barang (X) akan berhadapan dengan harganya (Px) Analisis hubungan antara harga dan permintaan barang. - Untuk memperoleh sejumlah barang diperlukan pengeluaran atau biaya (Z), yang dapat dihitung : -Z Dengan = Px. demikian, X ( Z sekarang = f(X) ) tujuan konsumen tidak semata-mata memaksisimumkan TU saja, tetapi harus memperhitungkan biayanya, yang berarti konsumen harus memaksimumkan selisih (S) antara TU dan Z (S = TU – Z), yaitu : by L 2 A 164 8

Maximize : S = TU - Z = f (X) Px. X Agar S maksimum , maka : Jika Px = 6, maka : X = 8 – 0, 5 Px X = 8 - 0, 5(6) = 5 TU = 16(5) – 52 = 55 Z = 6(X) = 30 S = TU – Z = 25 Dari contoh di atas, maka hukum permintaan terbukti : MUx = Px 16 – 2 X = Px X = 8 – 0, 5 Px ↓ X↑ by L 2 A 164 9

KONDISI KESEIMBANGAN KONSUMEN DENGAN KONSUMSI LEBIH DARI SATU BARANG - Untuk kondisi yang lebih nyata lagi, perilaku konsumen menghadapi berbagai pilihan barang dan terbatasnya dana yang dimiliki, TU = f (X 1, menghadapi X 2, . . Xn) harganya disamping C = Px 1 X 1 + Px 2 X 2. . + Pxn. Xn L = f (X 1, X 2, . . Xn) + ( ג C – Px 1 X 1 – Px 2 X 2. . – Pxn. Xn ) (Kondisi keseimbangan konsumen) by L 2 A 164

Contoh : Seorang konsumen diperkirakan mempunyai fungsi utilitas atas barang X dan Y seperti : TU = 10 X + 24 Y – 0, 5 X 2 – 0, 5 Y 2. Harga X (Px) = $2 dan harga Y (Py) = $6. Sedangkan dana yang dimilki sebesr $44. Pertanyaan : Berapa banyak barang X dan Y harus dibeli konsumen agar kepuasannya maksimum ? by L 2 A 164 11

Penyelesaian : Maksimumkan : TU = 10 X + 24 Y – 0, 5 X 2 – 0, 5 Y 2 Kendala : 44 = 2 X + 6 Y 44 = 2 X + 6(3 X 6) 44 = 20 X – 36 X = 4 Y = 3(4) – 6 = 6 by L 2 A 164 12

TU = 10(4) + 24(6) – 0, 5(42) – 0, 5(62) = 158 ( = ג 10 – 4)/2 = (24 – 6)/6 = 3 Jadi pembelian barang X = 4 unit dan Y = 6 unit, dan total kepuasannya sebanyak 158 utils. = ג 3 mengartikan pengaruh perubahan per $ terhadap fungsi TU (kepuasan), sebesar + 3 kali. Jadi kalau dana ditambah $10, maka TU akan bertambah sebesar +30 utils (3 x 10). Coba buktikan ! by L 2 A 164 13

Latihan : Tentukan kombinasi konsumsi barang X dan Y, sehingga kepuasan maksimum, jika : (a) TU = 12 X Y Px = $3, Py = $6 dan Dana = $60 (b) TU = 17 X + 20 Y – 2 X 2 – Y 2 Px = $3, Py = $6 dan Dana = $60 2 (c) TU = 18 X – X dan harga barang = Rp 8, -. Maka hitunglah : permintaan barang. by L 2 A 164 14