Teori Permainan q Teori Permainan game theory banyak

Teori Permainan q Teori Permainan [ game theory] banyak digunakan dalam analisis pemasaran atau perencanaan strategi perusahaan Konsep dasar teori permainan antara lain: 1. Ada pemain dengan sejumlah strateginya 2. Kemenangan bagi seorang pemain berarti kekalahan bagi pemain lainnya [ Zero-sum game] 3. Adanya kelangkaan sumber daya [ scarcity] 4. Pembacaan tabel permainan adalah dari baris ke kolom, nilai positif berarti kemenangan bagi pemain I, sekaligus kekalahan bagi pemain II. Sebaliknya, nilai negatif berarti kekalahan bagi pemain I, sekaligus kemenangan bagi pemain II. 5. Dimungkinkan adanya prinsip dominasi 6. Pemain I cenderung kepada strategi Maximin, sedangkan pemain II cenderung kepada strategi Minimax. 7. Bila nilai Maximin=minimax, berarti ada sadle point [permainan sudah pasti mengarah pad salah satu pilihan strategi saja, tidak perlu ada perhitungan lanjut] 8. Bila nilai maximin ≠ minimax, berarti ada mix strategi [ kedua pemain harus bertimbang dalam bentuk probabilitas untuk memainkan salah satu strateginya, harus dilakukkan perhitungan lanjut] By : Ary Prasetyo, ST

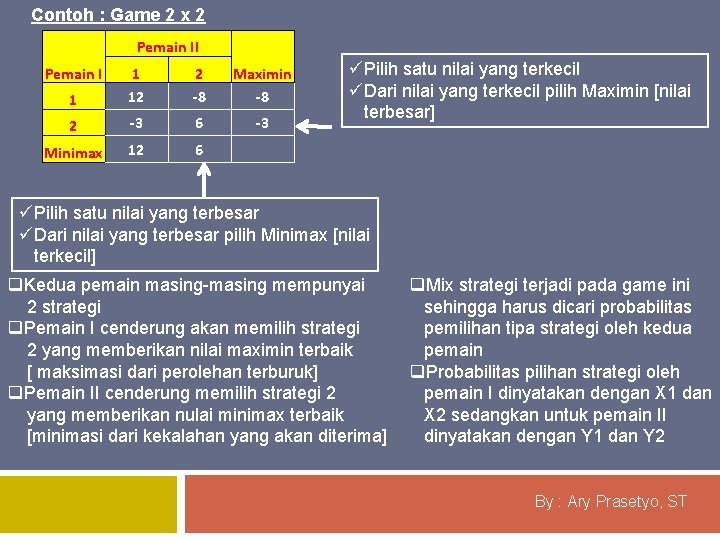
Contoh : Game 2 x 2 Pemain II 1 1 12 2 -8 Maximin -8 2 -3 6 -3 Minimax 12 6 Pemain I üPilih satu nilai yang terkecil üDari nilai yang terkecil pilih Maximin [nilai terbesar] üPilih satu nilai yang terbesar üDari nilai yang terbesar pilih Minimax [nilai terkecil] q. Kedua pemain masing-masing mempunyai 2 strategi q. Pemain I cenderung akan memilih strategi 2 yang memberikan nilai maximin terbaik [ maksimasi dari perolehan terburuk] q. Pemain II cenderung memilih strategi 2 yang memberikan nulai minimax terbaik [minimasi dari kekalahan yang akan diterima] q. Mix strategi terjadi pada game ini sehingga harus dicari probabilitas pemilihan tipa strategi oleh kedua pemain q. Probabilitas pilihan strategi oleh pemain I dinyatakan dengan X 1 dan X 2 sedangkan untuk pemain II dinyatakan dengan Y 1 dan Y 2 By : Ary Prasetyo, ST

Untuk menentukan X 1 dan X 2 serta Y 1 dan Y 2 digunakan Formula sbb: Pemain II Pemain I 1 [X 1] 1 [Y 1] 2 [Y 2] Maximin g[1, 1] 12 g[1, 2] -8 -8 g[2, 1] -3 -3 Untuk menentukan Y 1 dan Y 2 digunakan formula sbb: Y 2 = 1 –Y 1 g[1, 1] Y 1 + g[1, 2] Y 2 = g[2, 1] Y 1 + g[2, 2] Y 2 2 [X 2] 12 Y 1 – 8 [1 – Y 1] = - 3 Y 1 + 6 [1 – Y 1] 12 6 Minimax 12 Y 1 – 8 + 8 Y 1 = - 3 Y 1 + 6 – 6 Y 1] X 2 = 1 – X 1 20 Y 1 – 8 = - 9 Y 1 + 6 29 Y 1 = 14 g[1, 1] X 1 + g[2, 1] X 2 = g[1, 2] X 1 + g[2, 2] X 2 v. Y 1 = 14 / 29 12 X 1 - 3[1 – X 1] = -8 X 1 + 6[1 – X 1] v. Y 2 = 1 - 14/ 29 12 X 1 - 3 + 3 X 1 = -8 X 1 + 6 – 6 X 1 = 15 / 29 15 X 1 - 3 = -14 X 1 + 6 Probabilitas bagi pemain II untuk menggunakan 29 X 1 = 9 strategi 1 dan 2 berturut –turut Y 1 = 14/29 dan Y 2 = v. X 1 = 9 / 29 15/29 v. X 2 = 1 - 9 / 29 Probabilitas bagi pemain I untuk menggunakan strategi 1 dan 2 = 20 / 29 berturut –turut X 1 = 9/29 dan X 2 = 20/29 g[2, 2] 6 By : Ary Prasetyo, ST

Nilai Permainan [ game value] Dapat pula dihitung dengan: G* = 20 Y 1 – 8 = 20 [ 14/29] – 8 = 280/29 – 232/29 = 48/29 G* = 15 X 1 – 3 = 15 [ 9/29] – 3 = 135/29 – 87/29 = 48/29 Contoh : Game 2 x 4 dan ada dominasi Pemain II Pemain I 1 [X 1] 2 [X 2] Minimax 1 [Y 1] 2 [Y 2] 3 [Y 3] 4 [Y 4] Maximin 12 -5 12 -9 6 6 10 -8 10 -6 3 3 -9 -8 Bagaimana penyelesaiannya? q Game tersebut adalah mix strategi [karena nilai maximin berbeda dengan minimax] q Pada pembahasan kali ini semua strategi tetap dianalisis q Pemain I punya 2 alternatif strategi yang harus dihadapkan pada keempat strategi pemain II By : Ary Prasetyo, ST

q Hitunglah ekspektasi bagi pemain I, jika pemain II menggunakan keempat strategi Pemain II Pemain I 1 [X 1] 2 [X 2] Minimax Strategi Pemain II 1 2 3 4 1 [Y 1] 2 [Y 2] 3 [Y 3] 4 [Y 4] Maximin 12 -5 12 -9 6 6 10 -8 10 -6 3 3 -9 -8 Ekspektasi Nilai Bagi Pemain I 12 X 1 - 5 X 2 = 17 X 1 - 5 -9 X 1 + 6 X 2 = -15 X 1 + 6 10 X 1 - 8 X 2 = 18 X 1 - 8 -6 X 1 + 3 X 2= -9 X 1 + 3 [1] [2] [3] [4] q Gambar keempat garis pada grafik 2 dimensi untuk ekpektasi nilai bagi pemain I q Tentukkan Probabilitas pemilihan Strategi bagi pemain I [kriterianya adalah Maximin] sbb: By : Ary Prasetyo, ST

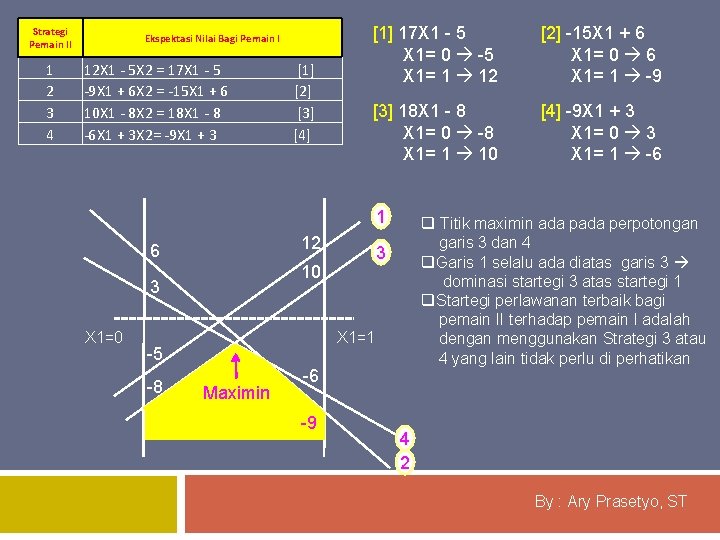
Strategi Pemain II 1 2 3 4 Ekspektasi Nilai Bagi Pemain I 12 X 1 - 5 X 2 = 17 X 1 - 5 -9 X 1 + 6 X 2 = -15 X 1 + 6 10 X 1 - 8 X 2 = 18 X 1 - 8 -6 X 1 + 3 X 2= -9 X 1 + 3 [1] [2] [3] [4] [1] 17 X 1 - 5 X 1= 0 -5 X 1= 1 12 [2] -15 X 1 + 6 X 1= 0 6 X 1= 1 -9 [3] 18 X 1 - 8 X 1= 0 -8 X 1= 1 10 [4] -9 X 1 + 3 X 1= 0 3 X 1= 1 -6 1 12 6 X 1=0 X 1=1 -5 -8 3 10 3 q Titik maximin ada perpotongan garis 3 dan 4 q. Garis 1 selalu ada diatas garis 3 dominasi startegi 3 atas startegi 1 q. Startegi perlawanan terbaik bagi pemain II terhadap pemain I adalah dengan menggunakan Strategi 3 atau 4 yang lain tidak perlu di perhatikan Maximin -6 -9 4 2 By : Ary Prasetyo, ST

q Probabilitas pemilihan strategi bagi pemain I 18 X 1 – 8 = -9 X 1 + 3 27 X 1 = 11/27 X 2 = 1 – 11/27 = 16/27 q Probabilitas pemilihan strategi bagi pemain II Pemain I 1 [X 1] 2 [X 2] Minimax 1 [Y 1] 2 [Y 2] 3 [Y 3] 4 [Y 4] Maximin 12 -5 12 -9 6 6 10 -8 10 -6 3 3 -9 -8 16 Y 3 - 6 = -11 Y 3 + 3 27 Y 3 = 9/27 Y 4 = 1 – 9/27 = 18/27 Y 1 =Y 2 =0 10 Y 3 – 6 Y 4 = 16 Y 3 - 6 -8 Y 3 + 3 Y 4 = -11 Y 3 + 3 q Nilai Permainan : G* = 18 X 1 – 8 = 18 [11/27] -8 = 198/27 – 216/27 = -18/27 Berarti Kemenangan untuk pemain II By : Ary Prasetyo, ST

Contoh : Game 4 x 2 dan ada dominasi Pemain I 1 [X 1] 2 [X 2] 3 [X 3] 4 [X 4] Minimax Pemain II 1 [Y 1] 2 [Y 2] -8 6 8 -3 5 -5 4 -2 8 6 q Game tersebut adalah mix strategi [karena nilai maximin berbeda dengan minimax] q Pada pembahasan kali ini semua strategi tetap dianalisis q Pemain I punya 4 alternatif strategi yang harus dihadapkan pada kedua strategi pemain II Maximin -8 -3 -5 -2 Bagaimana penyelesaiannya? q Hitunglah ekspektasi bagi pemain II, jika pemain I menggunakan keempat strategi Strategi Pemain I 1 2 3 4 Ekspektasi Nilai Bagi Pemain II -8 Y 1 + 6 Y 2 = -14 Y 1 + 6 8 Y 1 – 3 Y 2 = 11 Y 1 – 3 5 Y 1 – 5 Y 2 = 10 Y 1 - 5 4 Y 1 – 2 Y 2 = 6 Y 1 - 2 [1] [2] [3] [4] q Gambar keempat garis pada grafik 2 dimensi untuk ekpektasi nilai bagi pemain II q Tentukkan Probabilitas pemilihan Strategi bagi pemain II [kriterianya adalah Minimax] sbb: By : Ary Prasetyo, ST

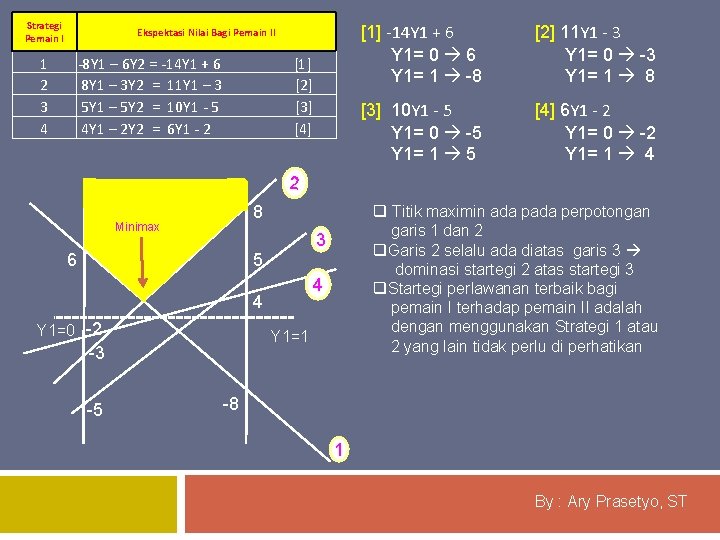
Strategi Pemain I Ekspektasi Nilai Bagi Pemain II 1 2 3 4 -8 Y 1 – 6 Y 2 = -14 Y 1 + 6 8 Y 1 – 3 Y 2 = 11 Y 1 – 3 5 Y 1 – 5 Y 2 = 10 Y 1 - 5 4 Y 1 – 2 Y 2 = 6 Y 1 - 2 [1] [2] [3] [4] [1] -14 Y 1 + 6 Y 1= 0 6 Y 1= 1 -8 [2] 11 Y 1 - 3 Y 1= 0 -3 Y 1= 1 8 [3] 10 Y 1 - 5 Y 1= 0 -5 Y 1= 1 5 [4] 6 Y 1 - 2 Y 1= 0 -2 Y 1= 1 4 2 8 Minimax q Titik maximin ada perpotongan garis 1 dan 2 q. Garis 2 selalu ada diatas garis 3 dominasi startegi 2 atas startegi 3 q. Startegi perlawanan terbaik bagi pemain I terhadap pemain II adalah dengan menggunakan Strategi 1 atau 2 yang lain tidak perlu di perhatikan 3 6 5 4 4 Y 1=0 -2 Y 1=1 -3 -5 -8 1 By : Ary Prasetyo, ST

q Probabilitas pemilihan strategi bagi pemain II -14 Y 1 + 6 = 11 Y 1 - 3 25 Y 1 = 9/25 Y 2 = 1 – 9/25 = 16/25 q Probabilitas pemilihan strategi bagi pemain I [antara strategi 1 dan 2] -16 X 1 + 8 = 9 X 1 – 3 Pemain II 25 X 1 = 11 Pemain I Maximin 1 [Y 1] 2 [Y 2] X 1 = 11/25 -8 6 -8 1 [X 1] X 2 = 1 – 11/25 8 -3 -3 2 [X 2] = 14/25 5 -5 -5 3 [X 3] 4 [X 4] Minimax 4 8 -2 6 -2 X 3 = X 4 =0 Nilai Permainan G* = 9 X 1 – 3 = 9 [11/25] - 3 = 24/25 Berarti Kemenangan untuk pemain I By : Ary Prasetyo, ST

Sekian dan Terimakasih By : Ary Prasetyo, ST