TEORI PERMAINAN PENGANTAR v Teori tentang permainan muncul

TEORI PERMAINAN

PENGANTAR v Teori tentang permainan muncul akibat adanya persaingan. v Persaingan terjadi antara dua individu atau dua kelompok. v Tetapi tidak semua persaingan dapat dikatakan sebagai sebuah permainan. v Hanya persaingan yang memenuhi beberapa kriteria yang dapat dikategorikan sebagai permainan Metode Stokastik Teori Permainan

Kriteria Permainan 1. Terdapat persaingan diantara pemain. 2. Setiap pemain mempunyai beberapa pilihan rencana yang dinamakan “strategi” 3. Aturan yang mengatur pilihan tersebut disebutkan satu persatu dan diketahui oleh para pemain. 4. Hasil permainan dipengaruhi oleh pilihan para pemain. Metode Stokastik Teori Permainan

Definisi permainan v Teori permainan adalah teori yang mengatur tentang persaingan antar dua individu atau kelompok dengan menggunakan aturan-aturan yang telah diketahui oleh kedua belah pihak. Metode Stokastik Teori Permainan

Aturan - Aturan v Terdapat sejumlah langkah atau strategi yang dapat dipilih oleh para pemain untuk dapat memenangkan permainan. v Terdapat informasi tentang strategi yang dipilih oleh pemain. v Pembayaran yang harus dipenuhi oleh setiap pemain di akhir permainan Metode Stokastik Teori Permainan

Jenis pembayaran v Pembayaran dalam bilangan positif berarti kemenangan untuk pihak pertama. v Pembayaran dalam bilangan negatif berarti kemenangan untuk pihak kedua. v Pembayaran dalam nilai nol berarti tidak ada pihak yang menang (permainan seri) Metode Stokastik Teori Permainan

Klasifikasi permainan (1) 1. Permainan berjumlah nol (Zero Sum Game), merupakan tipe permainan dengan karakteristik sbb : § Jumlah kemenangan kedua belah pihak sama dengan nol. § Jumlah pembayaran yang diterima oleh pemain yang menang sama dengan jumlah yang dibayarkan oleh pemain yang kalah. Metode Stokastik Teori Permainan

Klasifikasi permainan (2) § Kemenangan pihak yang satu merupakan kekalahan bagi pihak yang lainnya § Bila permainan dilakukan oleh dua orang, dinamakan Two Zero Sum Game. Metode Stokastik Teori Permainan

Klasifikasi permainan (3) 2. Permainan tidak berjumlah nol (Non Zero Sum Game), merupakan tipe permainan total pembayaran tidak sama dengan nol. Metode Stokastik Teori Permainan

Matriks Pembayaran v Matriks pembayaran (pay off matrix) merupakan matriks pembayaran yang dilakukan oleh strategi yang dimiliki oleh para pemain. v Pemain pertama memaksimumkan pemain kedua (baris) bertujuan pemasukkan (kolom) untuk sedangkan berusaha untuk meminimumkan pengeluaran Metode Stokastik Teori Permainan

Nilai permainan v Dari matriks pembayaran, dapat terlihat kedua belah pihak menentukan strategi yang optimal dan nilai permainannnya. v Strategi optimal adalah strategi yang menempatkan pemain dalam kondisi yg terbaik tanpa memperhitungkan kondisi pesaingnya. v Nilai permainan adalah nilai rata – rata pembayaran permainan jika kedua pihak telah menggunakan strategi optimalnya Metode Stokastik Teori Permainan

STRATEGI MURNI Penyelesaian dilakukan dengan menggunakan konsep maksimin untuk pemain baris dan minimaks untuk pemain kolom. Dalam strategi ini pemain akan menggunakan satu strategi tunggal untuk mendapat hasil optimal saddle point yang sama STRATEGI CAMPURAN Strategi ini dilakukan bila strategi murni belum memberi penyelesaian optimal. Sehingga perlu dilakukan tindak lanjut untuk mendapat titik optimal, dengan usaha mendapatkan saddle point yang sama. Metode Stokastik Teori Permainan

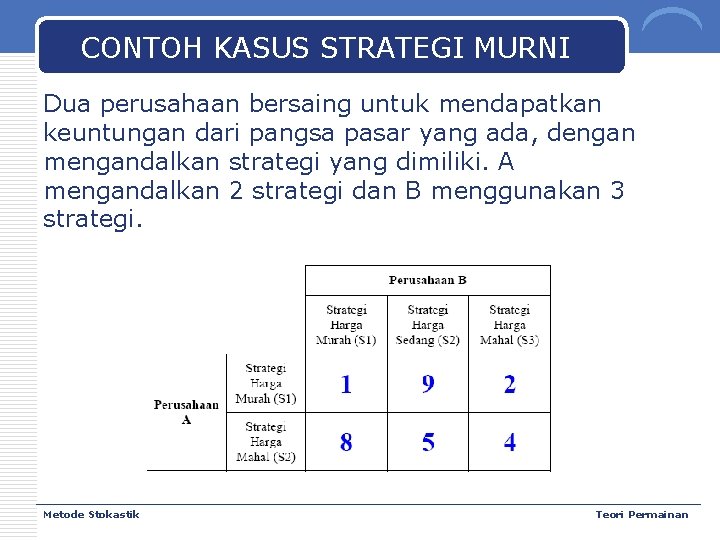
CONTOH KASUS STRATEGI MURNI Dua perusahaan bersaing untuk mendapatkan keuntungan dari pangsa pasar yang ada, dengan mengandalkan strategi yang dimiliki. A mengandalkan 2 strategi dan B menggunakan 3 strategi. Metode Stokastik Teori Permainan

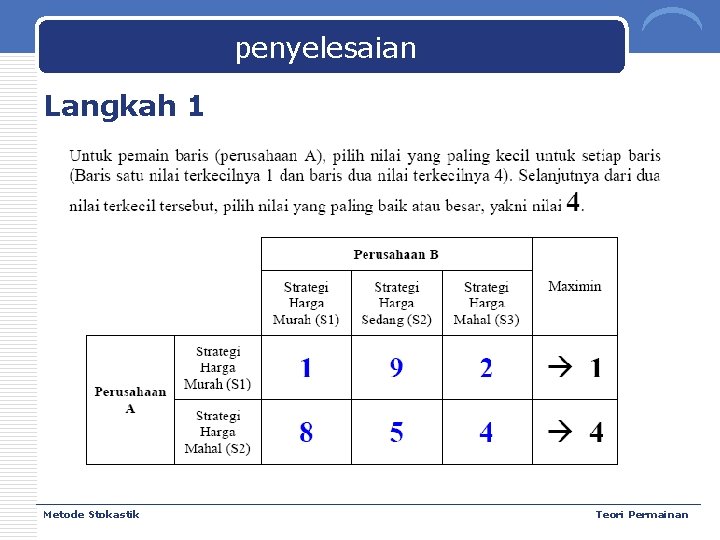
penyelesaian Langkah 1 Metode Stokastik Teori Permainan

penyelesaian Langkah 2 Metode Stokastik Teori Permainan

penyelesaian Langkah 3 Kesimpulan: v Pemain baris dan pemain kolom sudah memiliki pilihan strategi yang sama yaitu nilai 4 optimal v Pilihan tersebut berarti bahwa meskipun A menginginkan keuntungan yang lebih besar, tapi tetap hanya akan memperoleh keuntungan maksimal 4 dengan strategi harga mahal (S 2), demikian juga dengan B, kerugian yang paling minimal adalah 4, dengan merespon strategi A, dengan strategi harga mahal (S 3) v Penggunaan strategi lain berdampak menurunnya keuntungan A dan meningkatnya kerugian B Metode Stokastik Teori Permainan

CONTOH KASUS STRATEGI CAMPURAN Metode Stokastik Teori Permainan

penyelesaian Langkah 1 Cari maksimin dan minimaks terlebih dahulu seperti strategi murni Diperoleh angka penyelesaian berbeda, A 2, B 5 Metode Stokastik Teori Permainan

penyelesaian Langkah 2 v Masing-masing pemain menghilangkan strategi yang menghasilkan keuntungan dan kerugian terburuk v Bagi A, S 2 adalah strategi terburuk, karena dapat menimbulkan kerugian (ada nilai minus) v Bagi B, S 3 adalah paling buruk karena bisa menimbulkan kerugian terbesar Metode Stokastik Teori Permainan

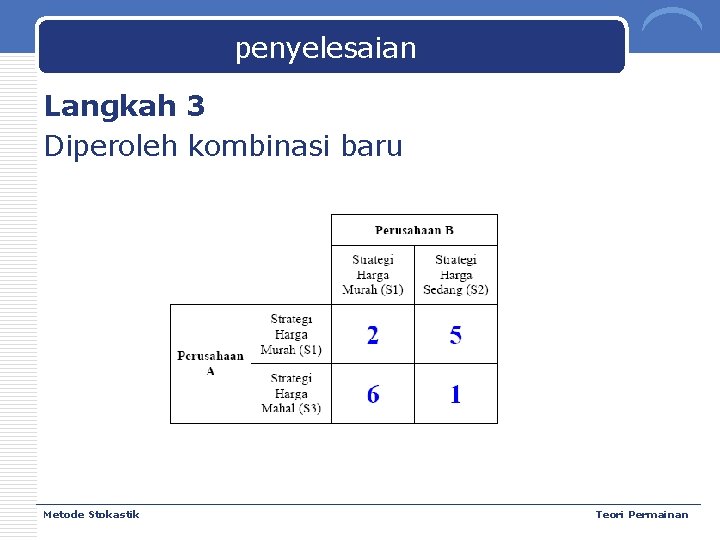
penyelesaian Langkah 3 Diperoleh kombinasi baru Metode Stokastik Teori Permainan

penyelesaian Langkah 4 Metode Stokastik Teori Permainan

penyelesaian Langkah 5 Mencari besaran probabilitas setiap strategi untuk menghitung saddle point yang optimal. Untuk perusahaan A Bila strategi A direspon B dengan S 1: 2 p + 6(1 -p) = 2 p + 6 – 6 p = 6 – 4 p Bila strategi A direspon B dengan S 2: 5 p + 1(1 -p) = 5 p + 1 – p = 1 + 4 p Bila digabung: 6 – 4 p = 1 + 4 p 5 = 8 p Metode Stokastik P = 5/8 = 0, 625 Teori Permainan

penyelesaian Apabila p = 0, 625, maka 1 – p = 0, 375 Masukkan nilai tersebut pada kedua persamaan Keuntungan yang diharapkan adalah sama = 3, 5, yang berarti memberikan peningkatan 1, 5 mengingat keuntungan A hanya 2 (langkah 1) Metode Stokastik Teori Permainan

penyelesaian Untuk perusahaan B Bila strategi B direspon A dengan S 1: 2 q + 5(1 – q) = 2 q + 5 – 5 q = 5 – 3 q Bila strategi B direspon A dengan S 2: 6 q + 1(1 – q) = 6 q + 1 – 1 q = 1 + 5 q Bila digabung: 5 – 3 q = 1 + 5 q 4 = 8 q q = 4/8 = 0, 5, maka 1 -q = 0, 5 Masukkan ke persamaan Metode Stokastik Teori Permainan

penyelesaian Kerugian minimal yang diharapkan sama, yaitu 3, 5. Pada langkah pertama kerugian minimal adalah 5, dengan demikian dengan strategi ini B bisa menurunkan kerugian sebesar 1, 5. Kesimpulan: Strategi campuran memberikan saddle point 3, 5. Nilai tersebut memberi peningkatan keuntungan bagi A dan penurunan kerugian B masing-masing sebesar 1, 5. Metode Stokastik Teori Permainan

Contoh kasus : A akan menebak uang pecahan Rp. 500 dan Rp. 1000 yang masing-masing ada di genggaman tangan sebelah kiri dan kanan B. Jika A menebak uang yang ada di tangan kiri B dengan Rp. 500 maka B akan membayar Rp. 500, tapi jika A menebak dengan Rp. 1000, maka A akan membayar Rp. 500. Inti dari permainan ini adalah : Jika A menebak secara benar, maka B membayar seharga dalam genggaman, tapi jika A salah maka A yang membayar seharga tersebut. Tentukan strategi buat A dan B Metode Stokastik Teori Permainan

Solusi : Strategi A Strategi 1 : Menebak Rp 500 di tangan kiri Strategi 2 : Menebak Rp 1000 di tangan kiri Strategi B Strategi 1 : Rp 500 di tangan kiri Strategi 2 : Rp 1000 di tangan kanan Metode Stokastik Teori Permainan

Pay of Matriks B A 1 2 1 500 -1000 2 -500 1000 Kesimpulan : v Strategi A menghasilkan nilai -500 (S 2) v Strategi B menghasilkan nilai 500 (S 1) v Strategi optimal diperoleh dengan strategi campuran Metode Stokastik Teori Permainan

Solusi A 1 (q) 1 (p) 500 2 (1 -p) -500 B 2 (1 -q) -1000 -500 1000 Pemain A Jika strategi A direspon oleh B dengan S 1 500 p + (-500(1 -p)) 500 p-500+500 p = 1000 p-500……. (1) Jika strategi A direspon oleh B dengan S 2 -1000 p + 1000(1 -p) -1000 p+1000 -1000 p = 1000 -2000 p……. (2) Metode Stokastik Teori Permainan

Solusi Persamaan 1 & 2 1000 p-500 = 1000 -2000 p 3000 p = 1500 p = 0. 5 Substitusikan nilai p ke persamaan 1 1000(0. 5)-500 = 0 Substitusikan nilai p ke persamaan 2 1000 -2000(0. 5) = 0 Kedua strategi menghasilkan nilai 0, artinya ada kenaikan keuntungan sebesar 500 dibandingkan strategi awal A Metode Stokastik Teori Permainan

Solusi A 1 (q) 1 (p) 500 2 (1 -p) -500 B 2 (1 -q) -1000 -500 1000 Pemain B Jika strategi B direspon oleh A dengan S 1 500 q + (-1000(1 -q)) 500 q-1000+1000 q = 1500 q-1000……. (1) Jika strategi B direspon oleh A dengan S 2 -500 q + 1000(1 -q) -500 q+1000 -1000 q = 1000 -1500 q……. (2) Metode Stokastik Teori Permainan

Solusi Persamaan 1 & 2 1500 q-1000 = 1000 -1500 q 3000 q = 2000 q = 0. 67 Substitusikan nilai p ke persamaan 1 1500(0. 67)-1000 = 0 Substitusikan nilai p ke persamaan 2 1000 -1500(0, 67) = 0 Kedua strategi menghasilkan nilai 0, artinya ada kenaikan keuntungan sebesar 500 dibandingkan strategi awal B Metode Stokastik Teori Permainan

Strategi Optimal Pemain A Peluang menggunakan strategi 1 = 0. 5 Peluang menggunakan strategi 2 = 0. 5 Pemain B Peluang menggunakan strategi 1 = 0. 67 Peluang menggunakan strategi 2 = 0. 33 Strategi optimal : Pemain A : Strategi 1 atau 2 Pemain B : Strategi 1 Metode Stokastik Teori Permainan

Pengembangan Model (1) Strategi A Strategi 1 : Menebak Rp 500 di tangan kiri Strategi 2 : Menebak Rp 1000 di tangan kiri Strategi B Strategi 1 : Rp 500 di tangan kiri dan Rp 1000 di tangan kanan Metode Stokastik Teori Permainan

Pay of Matriks B 1 A 1 1500 2 -1500 Kesimpulan : v Sadle point di titik 1500 v Strategi optimal A adalah strategi 1 dengan maksimal keuntungan Rp 1500 v Strategi optimal B adalah strategi 1 dengan minimal kerugian Rp 1500 Metode Stokastik Teori Permainan

Pengembangan Model (2) Strategi A Strategi 1 : Menebak Rp 500 di tangan kiri Strategi 2 : Menebak Rp 1000 di tangan kiri Strategi B Strategi 1 : Rp 500 di tangan kiri dan Rp 1000 di tangan kanan Strategi 2 : Rp 1000 di tangan kiri dan Rp 500 di tangan kanan Metode Stokastik Teori Permainan

Pay of Matriks B 1 A 2 1 1500 -1500 2 -1500 1500 Kesimpulan : v Strategi A menghasilkan nilai -1500 v Strategi B menghasilkan nilai 1500 v Strategi optimal diperoleh dengan strategi campuran 8 Metode Stokastik Teori Permainan

Solusi A B 1 (q) 2 (1 -q) 1 (p) 1500 -1500 2 (1 -p) -1500 1500 Pemain A Jika strategi A direspon oleh B dengan S 1 1500 p + (-1500(1 -p)) 1500 p-1500+1500 p = 3000 p-1500……. (1) Jika strategi A direspon oleh B dengan S 2 -1500 p + 1500(1 -p) -1500 p+1500 -1500 p = 1500 -3000 p……. (2) Metode Stokastik Teori Permainan

Solusi Persamaan 1 & 2 3000 p-1500 = 1500 -3000 p 6000 p = 3000 p = 0. 5 Substitusikan nilai p ke persamaan 1 3000(0. 5)-1500 = 0 Substitusikan nilai p ke persamaan 2 1500 -3000(0. 5) = 0 Kedua strategi menghasilkan nilai 0, artinya ada kenaikan keuntungan sebesar 1500 dibandingkan strategi awal A Metode Stokastik Teori Permainan

Solusi A B 1 (q) 2 (1 -q) 1 (p) 1500 -1500 2 (1 -p) -1500 1500 Pemain B Jika strategi B direspon oleh A dengan S 1 1500 q + (-1500(1 -q)) 1500 q-1500+1500 q = 3000 q-1500……. (1) Jika strategi B direspon oleh A dengan S 2 -1500 q + 1500(1 -q) -1500 q+1500 -1500 q = 1500 -3000 q……(2) Metode Stokastik Teori Permainan

Solusi Persamaan 1 & 2 3000 q-1500 = 1500 -3000 q 6000 q = 3000 q = 0. 5 Substitusikan nilai q ke persamaan 1 3000(0. 5)-1500 = 0 Substitusikan nilai q ke persamaan 2 1500 -3000(0. 5) = 0 Kedua strategi menghasilkan nilai 0, artinya ada penurunan kerugian sebesar 1500 dibandingkan strategi awal B Metode Stokastik Teori Permainan

Strategi Optimal Pemain A Peluang menggunakan strategi 1 = 0. 5 Peluang menggunakan strategi 2 = 0. 5 Pemain B Peluang menggunakan strategi 1 = 0. 5 Peluang menggunakan strategi 2 = 0. 5 Strategi optimal : Pemain A : Strategi 1 atau 2 Pemain B : Strategi 1 atau 2 Metode Stokastik Teori Permainan