TEORI PELUANG Pengantar Peluang muncul dikarenakan kesenangan orang

TEORI PELUANG

Pengantar • Peluang muncul dikarenakan kesenangan orang untuk mengadu peruntungan di atas meja judi. • Banyak teori yang muncul dari kegiatan judi tersebut yang sedikit banyak berpengaruh pada perkembangan ilmu statistik. • Peluang sendiri dalam dunia bisnis banyak berperan dalam proses pengambilan keputusan bisnis.

• “Probabilitas atau peluang diartikan sebagai suatu ukuran yang menyatakan tentang kemungkinan atau kesempatan terjadinya suatu peristiwa. ” • Peluang atau probabilitas dapat dinyatakan secara kualitatif (dalam bentuk pernyataan) atau secara kuantitatif ( dalam bentuk angka baik desimal maupun pecahan) • Probabilitas dinyatakan dalam bentuk pecahan antara 0 sampai 1 (selalu positif). 0 berarti peristiwa tidak terjadi sedangkan 1 menunjukan peristiwa pasti terjadi

• Terdapat 3 hal yang penting dalam probabilitas 1. Percobaan pengamatan terhadap beberapa peristiwa atau proses yang memungkinkan timbulnya paling sedikit 2 peristiwa tanpa memperhatikan peristiwa mana yang akan terjadi ( ex : percobaan melempar uang) 2. Hasil / Outcome hasil dari sebuah percobaan ( ex: muncul gambar / angka) 3. Peristiwa kumpulan satu atau lebih hasil yang terjadi pada suatu percobaan atau pengamatan ( ex : kalau tidak gambar berarti angka)

Pendekatan Probabilitas / Peluang • PENDEKATAN KLASIK sebuah peristiwa memiliki kesempatan yang sama untuk terjadi PROBABILITAS PERISTIWA = JUMLAH KEMUNGKINAN HASIL JUMLAH TOTAL KEMUNGKINAN HASIL

Percobaan Hasil Probabilitas Kegiatan melempar uang 1. Muncul gambar 2. Muncul angka 2 ½ Kegiatan perdagangan saham 1. Menjual saham 2. Membeli saham 2 ½ Perubahan harga 1. Inflasi (harga naik) 2. Deflasi (harga turun) 2 ½ Mahasiswa belajar 1. Lulus memuaskan 2. Lulus sangat memuaskan 3. Lulus terpuji 3 1/3

• Peristiwa saling lepas : “terjadinya suatu peristiwa sehingga peristiwa yang lain tidak terjadi pada waktu yg bersamaan (mutually exclusive)” Misal : dalam satu percobaan akan muncul peristiwa A dan B, , , jika A terjadi maka B tidak terjadi, begitu juga sebaliknya. Dalam suatu percobaan setidaknya semua hasil memiliki probabilitas yang sama, dan paling tidak akan ada 1 peristiwa yang terjadi (“lengkap terbatas kolektif”)

• PENDEKATAN RELATIF dalam pendekatan ini, besarnya probabilitas suatu peristiwa tidak dianggap sama tetapi tergantung pada berapa banyak suatu peristiwa terjadi dari keseluruhan percobaan atau kegiatan yang dilakukan. Probabilitas suatu peristiwa = Jumlah peristiwa yang terjadi Jumlah total percobaan Contoh : Dari 700 wisudawan UDINUS periode Maret 2020, 100 anak menyandang predikat terpuji, 200 anak dengan predikat sangat memuaskan, dan 400 anak berpredikat memuaskan. Maka probabilitas anak dengan predikat terpuji adalah 100/700 = 0, 143 ; lulus dengan sangat memuaskan 200/700 = 0, 286, dan predikat memuaskan 400/700 = 0, 571

• PENDEKATAN SUBJEKTIF menyatakan probabilitas berdasarkan pada penilaian pribadi berdasar derajat kepercayaan

Konsep Dasar dan Hukum Probabilitas • Probabilitas dilambangkan dengan P, misal apabila kejadian menjual saham dilambangkan dengan A, maka probabilitas jual saham dinyatakan dengan P(A), sedangkan probabilitas beli saham dinyatakan dengan P(B)

1. Hukum Penjumlahan • Menyatakan bahwa “ probabilitas suatu kejadian atau probabilitas kejadian lain sama dengan penjumlahan probabilitas masing kejadian. • P(A ATAU B) = P(A) + P(B) • Contoh : P(A) = 0, 35, P(B) 0, 40 DAN P (C) 0, 25 Maka P(A ATAU C ) = 0, 35 + 0, 25 = 0, 60

2. Peristiwa atau Kejadian Bersama A AB B P(A ATAU B) = P(A) + P(B) – P (AB) Contoh : Diketahui probabilitas terjadinya A = 0, 6, probabilitas B = 0. 35 dan probabilitas AB secara bersamaan = 0, 15. Maka ; P(A atau B) = P(A) + P(B) – P(AB) P(A atau B) = 0, 6 + 0, 35 – 0, 15 = 0, 8

3. Kejadian Saling Lepas ( Mutually Exclusive ) A B • Dari diagram venn diatas menunjukkan bahwa peristiwa A dan peristiwa B saling lepas, artinya bahwa tidak ada bagian A yang menjadi bagian B, begitu juga sebaliknya sehingga P(AB) = 0 • P(A atau B) = P(A) + P(B) – P(AB) P(A) + P(B) -0 P(A) + P(B)

4. Hukum Perkalian • “Menghendaki bahwa semua peristiwa adalah independen ( suatu peristiwa atau kejadian tidak mempengaruhi probabilitas terjadinya peristiwa yang lain)”. • P (A dan B) = P(A) x P(B) • Contoh : Apabila kita melakukan pelemparan uang logam 2 kali ke udara, ditanyakan probabilitas kedua lemparan menghasilkan gambar? Probabilitas gambar = ½ dan probabilitas angka = ½. Pada lemparan 1 probabilitas gambar =1/2, pada lemparan kedua juga ½. Sehingga probabilitas P(A) dan P(B) adalah P(A dan B) = P(A) x P(B) =½x½ =¼

5. PROBABILITAS BERSYARAT • “ Probabilitas suatu peristiwa akan terjadi dengan ketentuan peristiwa yang lain telah terjadi” P (A|B) • Persamaan tersebut menunjukkan bahwa peristiwa A akan terjadi dengan syarat peristiwa B telah terjadi, artinya bahwa peristiwa B berpengaruh terhadap terjadinya peristiwa A, dalam persamaan dinyatakan sbb : P(A|B) = , dimana P(B) > 0 P(B|A) = , dimana P(A) > 0

• Untuk peristiwa bersyarat, P ( A dan B) = P(A) x P(B|A) P (B dan A) = P(B) x P(A|B)

Contoh • Sebuah perusahaan membuka lowongan kerja untuk mengisi pekerjaan sebagai sekretaris perusahaan. Ada 100 orang pelamar yang terdiri atas berpengalaman > 3 th dan <3 th dengan status menikah dan tidak menikah. Secara rinci jumlahnya adl sbb : • Menikah Tdk menikah Jumlah Pengalaman >3 th 12 24 36 Pengalaman <3 th 18 46 64 30 70 100 JUMLAH • Misal : E = peristiwa pelamar yang memiliki pengalaman >3 th M = peristiwa pelamar yang dipilih statusnya menikah

Jumlah titik dalam ruang sampel adalah S = 100 P(E) = 36 / 100 = 0, 36 P(M) = 30/100 = 0, 3 P(E∩M) = 12/100 = 0, 12 Selanjutnya dikarenakan sesuatu hal, pelamar hanya dibatasi pada pendaftar yang berstatus menikah. Selanjutnya perusahaan ingin mengetahui peluang terpilihnya pelamar dengan pengalaman lebih dari 3 tahun, , , notasinya adalah P(E|M). Dari tabel diketahui bahwa titik sampel menjadi 30, dan dengan menganggap bahwa peluang setiap pelamar adalah sama, maka : P(E|M) = 12/30 = 0, 4

6. PERISTIWA PELENGKAP • Menunjukkan bahwa apabila ada 2 peristiwa A dan B yang saling melengkapi, sehingga peristiwa A tidak terjadi, maka peristiwa B pasti terjadi. • Probabilitasnya P(A) + P(B) = 1 atau P(A) = 1 – P(B)

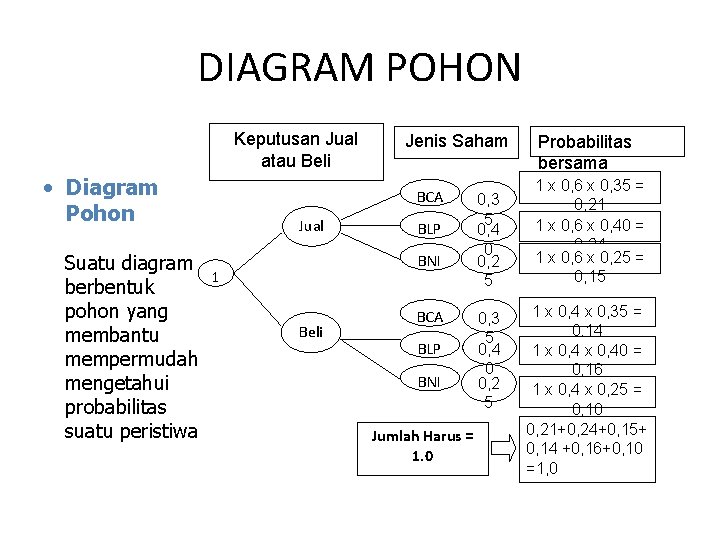
DIAGRAM POHON Keputusan Jual atau Beli • Diagram Pohon Suatu diagram berbentuk pohon yang membantu mempermudah mengetahui probabilitas suatu peristiwa Jenis Saham BCA Jual BLP BNI 1 Beli BCA BLP BNI Jumlah Harus = 1. 0 0, 3 5 0, 4 0 0, 2 5 Probabilitas bersama 1 x 0, 6 x 0, 35 = 0, 21 1 x 0, 6 x 0, 40 = 0, 24 1 x 0, 6 x 0, 25 = 0, 15 1 x 0, 4 x 0, 35 = 0, 14 1 x 0, 40 = 0, 16 1 x 0, 4 x 0, 25 = 0, 10 0, 21+0, 24+0, 15+ 0, 14 +0, 16+0, 10 =1, 0

Theorema Bayes • Merupakan probabilitas bersyarat, kejadian yang terjadi setelah kejadian lain ada P(Ai|B) = P(Ai) X P (B|Ai) P(A 1) X P(B|A 1)+P(A 2) X P(B|A 2) + … + P(Ai) X P(B|AI)

Prinsip Menghitung 1. Faktorial digunakan untuk mengetahui berapa banyak cara yang mungkin digunakan dalam mengatur sesuatu dalam kelompok. - Dilambangkan dengan (!) - n! = n x (n-1) x (n-2) x. . . X 2 x 1

2. Permutasi Digunakan untuk mengetahui sejumlah kemungkinan susunan jika terdapat satu kelompok objek

3. Kombinasi dipergunakan apabila kita tertarik pada berapa cara sesuatu diambil dari keseluruhan objek tanpa memperhatikan urutannya.