TEORI KEGAGALAN FAILURE THEORIES v TEORI TEGANGAN NORMAL































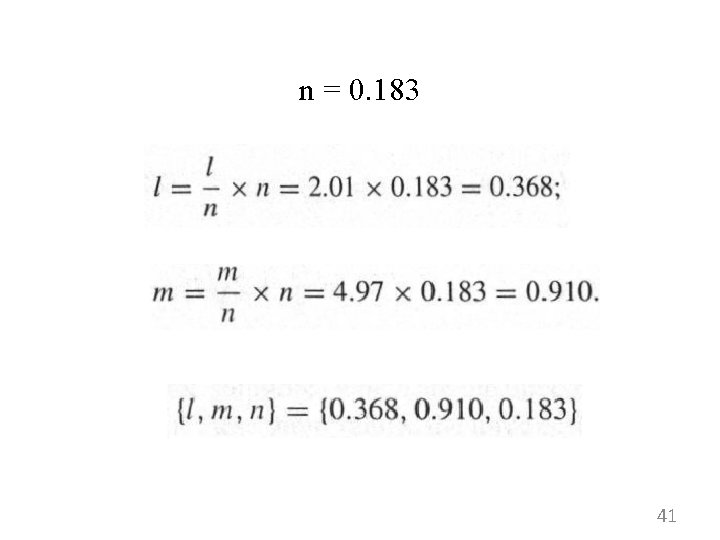


- Slides: 44

TEORI KEGAGALAN (FAILURE THEORIES) v TEORI TEGANGAN NORMAL MAKSIMUM (RANKINE) v TEORI TEGANGAN GESER MAKSIMUM (TRESCA) v TEORI ENERGI DISTORI (VON MISES) v TEORI REGANGAN NORMAL MAKSIMUM (ST. VENANT) v DLL. 1

TEORI TEGANGAN NORMAL MAKSIMUM (RANKINE) • Berdasarkan hasil eksperimen insinyur Inggris W. J. M. Rankine Teory Tegangan Normal Maksimum (Maximum Normal Stress Theory) • Kegagalan suatu material terjadi bila tegangan normal maksimum mencapai suatu harga tegangan luluh atau tegangan patahnya, tanpa memperhatikan tegangan utama (principal stress) lainnya. • Kriteria ini cocok untuk material getas ( brittle materials) 2

Tegangan 2 Dimensi (Biaxial Stress) : 3

TEORI TEGANGAN GESER MAKSIMUM (TRESCA) • Kriteria ini didahului pertama kali oleh C. A. Coulomb (1773) dan kemudian oleh H. Tresca (1864) Kriteria Tresca (Tresca Criterion) • Suatu material yang mendapat beban tegangan biaxial atau tegangan triaxial dinyatakan gagal bila tegangan geser maksimum yang terjadi pada setiap titik mencapai tegangan luluh geser dari material tersebut • Tegangan luluh geser = ½ tegangan luluh tarik typ = ½ syp • Kriteria ini cocok untuk material ulet (ductile materials) 4

Tegangan 2 dan 3 Dimensi : Kondisi tegangan biaxial Kondisi tegangan multiaxial 5

TEORI ENERGI DISTORI (HUBER-VON MISES-HENCKY) • Teori ini didahului oleh M. T. Huber di Polandia (1904) dan secara bebas dikembangkan oleh R. Von Mises di Jerman (1913) dan Hencky (1925) • Kegagalan diprediksi muncul dalam kondisi beban tegangan multiaxial bila energi distorsi per satuan volume menjadi sama atau melebihi energi distorsi per satuan volume pada saat gagalnya material uji. • Kriteria ini cocok untuk material ulet yang mendapat beban tegangan biaxial atau triaxial 6

Tegangan 3 Dimensi (Multiaxial Stress) : Atau : Bila : 7

TEORI REGANGAN NORMAL MAKSIMUM (ST. VENANT) • Teori ini dipropose oleh St. Venant khususnya berlaku untuk material getas (brittle material) • Kegagalan diprediksi muncul dalam kondisi tegangan multiaxial bila regangan normal utama maksimum (maximum principal normal strain) sama atau melebihi regangan normal maksimum pada saat material uji gagal. 8

Tegangan 3 Dimensi (Multiaxial Stress) e 1, e 2, e 3 = regangan normal ef utama = regangan patah 9

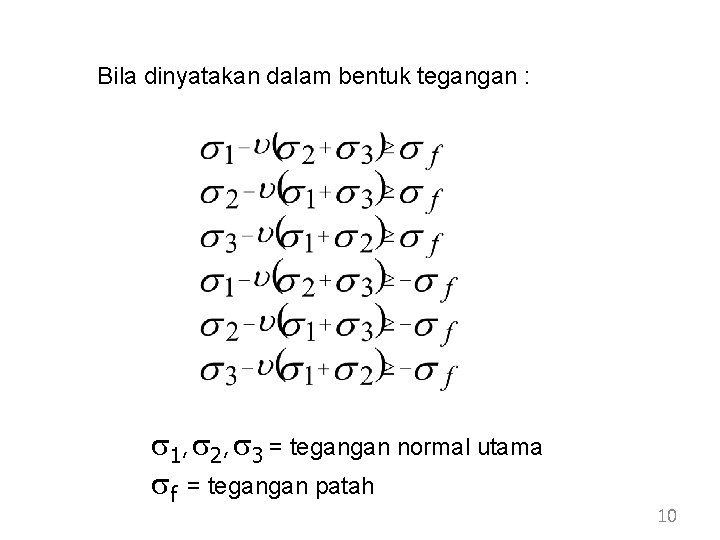
Bila dinyatakan dalam bentuk tegangan : s 1, s 2, s 3 = tegangan normal utama sf = tegangan patah 10

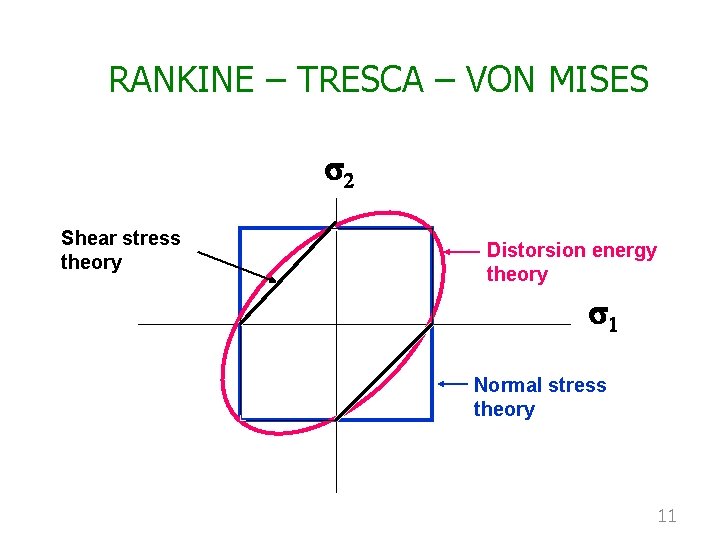
RANKINE – TRESCA – VON MISES s 2 Shear stress theory Distorsion energy theory s 1 Normal stress theory 11

CONTOH SOAL 1 : Sebuah poros berdiameter 50 mm mendapat beban tekan aksial sebesar 200 k. N dan momen puntir sebesar 2 k. Nm secara simultan. Ditanyakan: a) Gambar kondisi tegangan pada elemen kubus dari poros b) Matriks tegangan pada elemen kubus c) Tegangan utama yang bekerja pada silinder tersebut d) Tegangan geser maksimum yang terjadi pada silinder tersebut 12

Penyelesaian : Gaya tekan aksial akan menimbulkan tegangan tekan aksial sebesar : Tegangan geser yang terjadi pada bagian terluar dari poros adalah terbesar , dihitung dengan menggunakan rumus : T = momen puntir r = jari-jari silinder J = momen kelembaman polar luasan silinder 13

Tegangan geser yang terjadi pada bagian terluar dari poros : Sebuah elemen pada permukaan terluar dari poros akan mempunyai tegangan geser paling besar seperti ditunjukkan pada gambar di bawah ini. 14

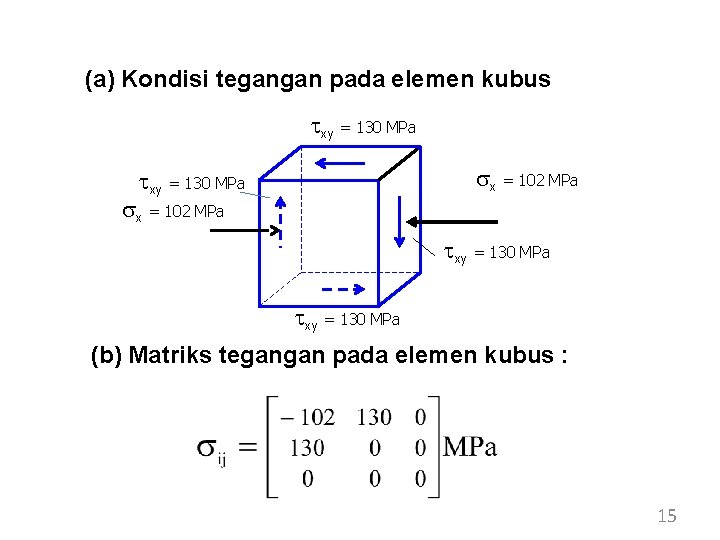
(a) Kondisi tegangan pada elemen kubus txy = 130 MPa sx = 102 MPa txy = 130 MPa (b) Matriks tegangan pada elemen kubus : 15

(c) Tegangan utama : (d) Tegangan geser maksimum : 16

SOAL 2 : Suatu silinder berdinding tipis mendapat beban kombinasi kearah tarik dan puntir secara bersamaan. Silinder tersebut mempunyai diameter = 400 mm dan tebal dinding = 2 mm. Silinder menerima beban tarik sebesar 200 k. N dan beban puntir sebesar 50 k. Nm secara simultan. Ditanyakan : a) Gambar kondisi tegangan pada elemen kubus dari dinding silinder b) Matriks tegangan pada elemen kubus tersebut c) Tegangan utama yang bekerja pada silinder tersebut d) Tegangan geser maksimum yang terjadi pada silinder tersebut e) Menurut kriteria luluh Rankine, Tresca, Von Mises bagaimana kondisi material tersebut bila material mempunyai tegangan luluh sebesar 350 MPa? 17

Penyelesaian : (a) (b) Tegangan tarik aksial sebesar 200 MPa menghasilkan distribusi tegangan yg uniform sepanjang silinder sebesar : Tegangan tarik tersebut bekerja pada setiap penampang seperti pd gbr (a) 18

Tegangan geser akibat beban puntir dihitung dengan menggunakan rumus : T = momen puntir r = jari-jari silinder J = momen kelembaman polar luasan silinder Silinder dinding tipis harga J adalah : 19

Tegangan geser pada silinder dinding tipis : Tegangan geser txy terlihat pada gambar (b) diatas. Dari hasil perhitungan diatas diperoleh tegangan yang bekerja pada silinder dinding tipis adalah : sx = 79, 6 MPa txy = 100 MPa 20

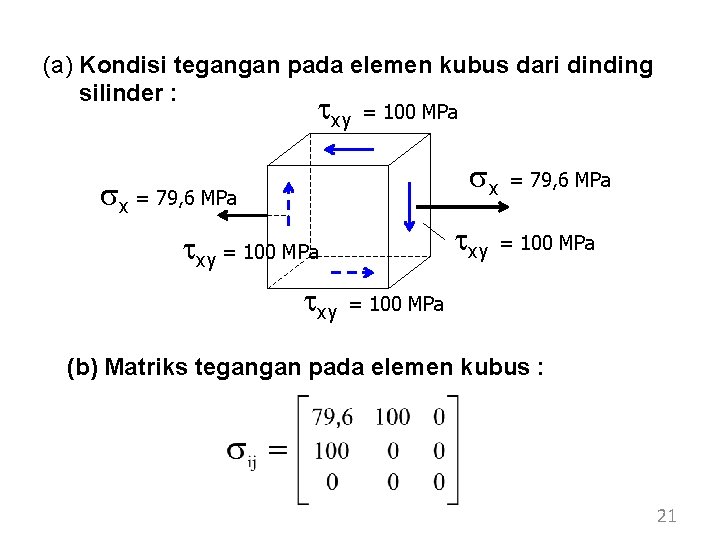
(a) Kondisi tegangan pada elemen kubus dari dinding silinder : txy = 100 MPa sx sx = 79, 6 MPa txy = 100 MPa txy = 79, 6 MPa = 100 MPa (b) Matriks tegangan pada elemen kubus : 21

Tegangan tarik simultan : sx dan tegangan geser txy bekerja secara sx = 79, 6 MPa , txy = 100 MPa (c) Tegangan utama : 22

(d) Tegangan geser maksimum : 23

(e) Kondisi material menurut Kriteria Luluh Rankine, Tresca dan Von Mises : Kriteria Tegangan Normal Maksimum (Rankine) : smaks = 147, 4 MPa < 350 MPa material belum luluh Kriteria Tegangan Geser Maksimum (Tresca) : Tegangan luluh geser = 0, 5 tegangan luluh tarik = 0, 5 x 350 MPa = 175 MPa tmaks = 107, 7 MPa < 175 MPa material belum luluh 24

Kriteria Von Mises : material belum luluh 25

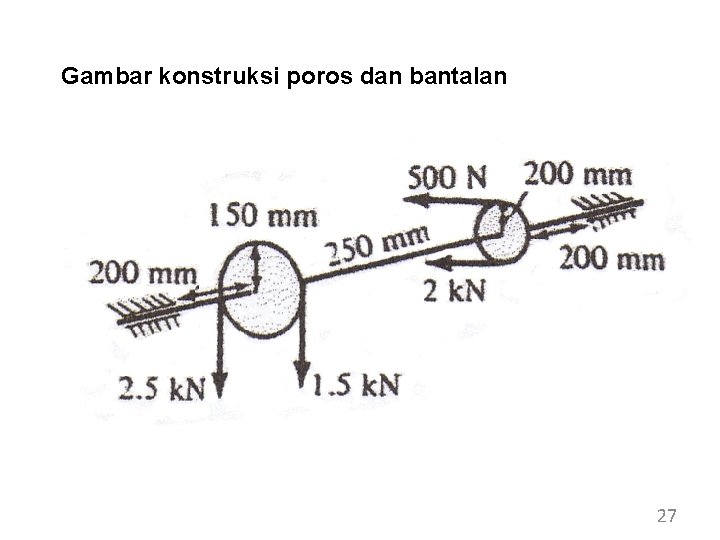
SOAL 3 : Sebuah poros berdiameter 30 mm berputar dengan kecepatan sudut konstan (seperti terlihat pada gambar dibawah ini). Sabuk (belt) pada pulley memberi beban kombinasi bending dan torsi pada poros. Berat poros dan pulley diabaikan, asumsikan bahwa bantalan pada poros hanya memberikan gaya reaksi arah melintang. Ditanyakan: a) Gambar diagram benda bebas pada konstruksi poros dan bantalan b) Gambar diagram bidang momen pada poros akibat beban bending dan torsi c) Tegangan utama yang bekerja pada poros tersebut 26

Gambar konstruksi poros dan bantalan 27

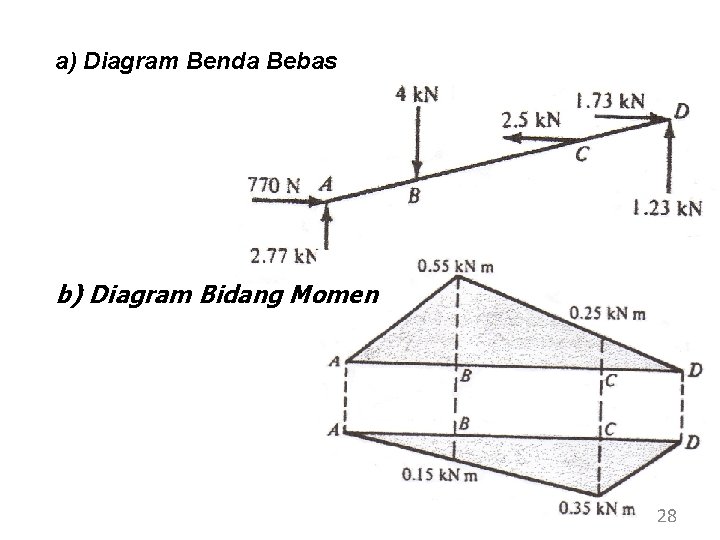
a) Diagram Benda Bebas b) Diagram Bidang Momen 28

Resultan momen bending di B dan C : Momen puntir (torsi) antara 2 pulley adalah konstan : 29

Momen puntir (torsi) di B dan C adalah sama elemen kritis pada poros terdapat pada titik B Tegangan bending maksimum di B : Tegangan geser maksimum di B : 30

c) Tegangan utama (principal stress) : 31

SOAL 4 : Sebuah konstruksi poros pejal berbentuk bulat yang ditumpu oleh dua buah bantalan. Pada kedua ujungnya mendapat beban tarik oleh dua buah sabuk yang bekerja pada pulley seperti terlihat pada gambar (a) dibawah ini. Bila poros tersebut terbuat dari material yang mempunyai tegangan luluh 250 MPa, maka dengan menggunakan teori tegangan normal maksimum dan angka keamanan 3 hitung diameter poros supaya tahan terhadap beban diatas. 32

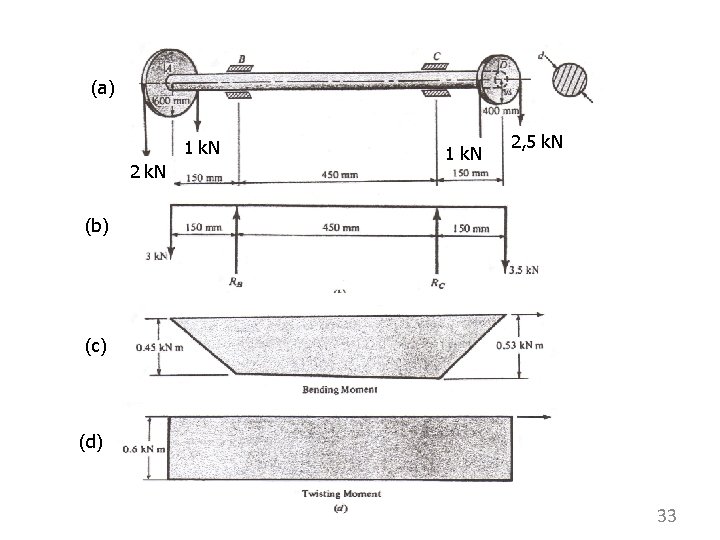
(a) 1 k. N 2 k. N 1 k. N 2, 5 k. N (b) (c) (d) 33

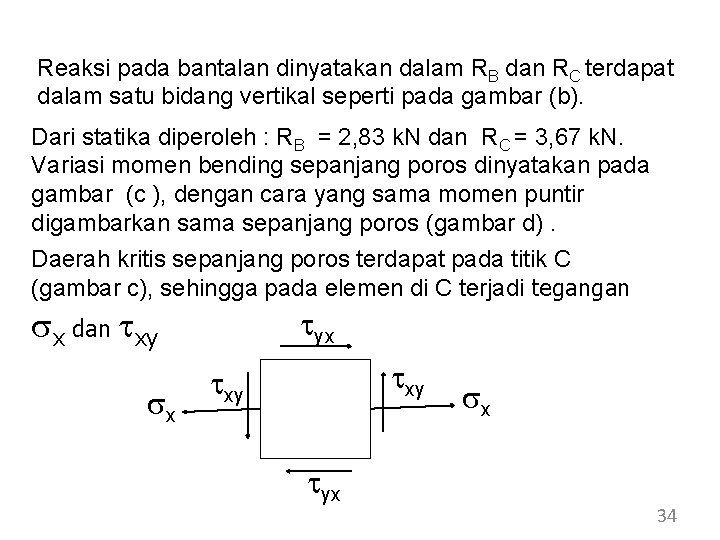
Reaksi pada bantalan dinyatakan dalam RB dan RC terdapat dalam satu bidang vertikal seperti pada gambar (b). Dari statika diperoleh : RB = 2, 83 k. N dan RC = 3, 67 k. N. Variasi momen bending sepanjang poros dinyatakan pada gambar (c ), dengan cara yang sama momen puntir digambarkan sama sepanjang poros (gambar d). Daerah kritis sepanjang poros terdapat pada titik C (gambar c), sehingga pada elemen di C terjadi tegangan sx dan txy sx tyx txy tyx sx 34

Tegangan normal akibat bending : (1) Tegangan normal yang lain : sy dan sz = 0 Tegangan geser txy muncul akibat beban puntir dari tarikan sabuk pulley : (2) 35

Tegangan normal maksimum diperoleh dari tegangan utama maksimum dengan rumus : (3) Substitusi pers (1), (2), dan (3), dengan menggunakan angka keamanan 3, maka : Dari persamaan diatas diperoleh d = 43 mm 36

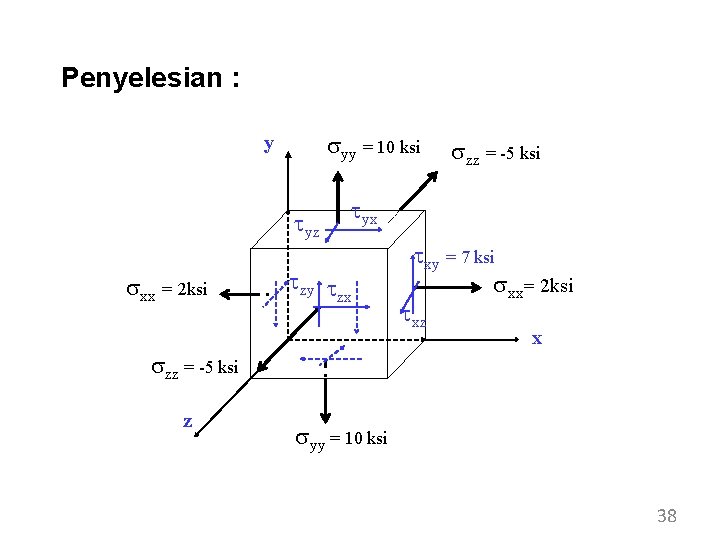
SOAL 5 Sebuah elemen kecil pada suatu komponen mendapat beban multiaxial sebagai berikut : Ditanyakan : a) Gambar kondisi tegangan multiaxial pada elemen kubus tersebut b) Besar tegangan utama yg terjadi akibat pembebanan multiaxial tsb. c) Cos arah (l, m, n) dari tegangan utama 37

Penyelesian : syy = 10 ksi y tyz sxx = 2 ksi szz = -5 ksi tyx tzy t zx txy = 7 ksi sxx= 2 ksi txz x szz = -5 ksi z syy = 10 ksi 38

sxx = 2 ksi , syy = 10 ksi, szz = -5 ksi, txy = 7 ksi, tyz = 5 ksi, tzx = -3 ksi dimana koefisien invarian I 1, 2, 3 adalah : I 1 = (sxx + I 2 syy + szz) = 3 ksi = (sxxsyy + syyszz+ sxxszz – txy 2 – tyz 2–txz 2) = - 143 (ksi)2 I 3 = (sxxsyyszz + 2 txytyztxz – sxxtyz 2 – syytxz 2 - szztxy 2) = 95 (ksi)3 Sehingga : 39

Arah tegangan utama 40
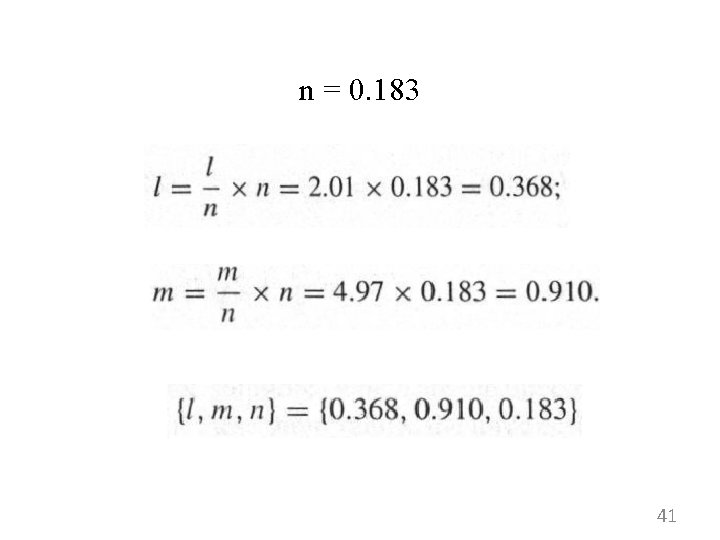
n = 0. 183 41

SOAL LATIHAN SOAL 1 : Sebuah komponen dibuat dari bahan baja St 60 mendapat beban multiaksial sbb : tegangan tarik ke arah sb x dan sb y sebesar 50 kg/mm 2 dan 10 kg/mm 2, tegangan tekan ke arah sb Z sebesar 20 kg/mm 2, tegangan geser pada bid x ke arah sb z sebesar 30 kg/mm 2 Bila material tersebut mempunyai tegangan luluh = 55 kg/mm 2, maka ditanyakan : a) Gambar kondisi tegangan pada suatu titik (elemen kubus) b) Matriks tegangan yang bekerja pada elemen kubus tersebut c) Menurut kriteria luluh Rankine, Tresca dan Von Mises, bagaimana kondisi material tersebut pada saat menerima beban tegangan? 42

SOAL 2 : Sebuah silinder berdinding tipis mempunyai diameter 250 mm dan tebal dinding 2, 5 mm. Di dalam silinder tersebut mendapat tekanan yang seragam (uniform) sebesar 1 MPa. Berapa gaya tarik axial yang bekerja pada dinding silinder tersebut secara simultan tanpa tegangan tarik maksimum melebihi 150 MPa? SOAL 3 : Sebuah silinder berdinding tipis mendapat gaya tekan axial 200 k. N dan momen torsi 3 k. Nm secara simultan. Diameter silinder adalah 300 mm dan tebal dinding silinder 3 mm. Tentukan tegangan utama yang terjadi pada elemen dinding silinder dan tegangan geser maksimumnya. Abaikan kemungkinan terjadi buckling pada silinder. 43

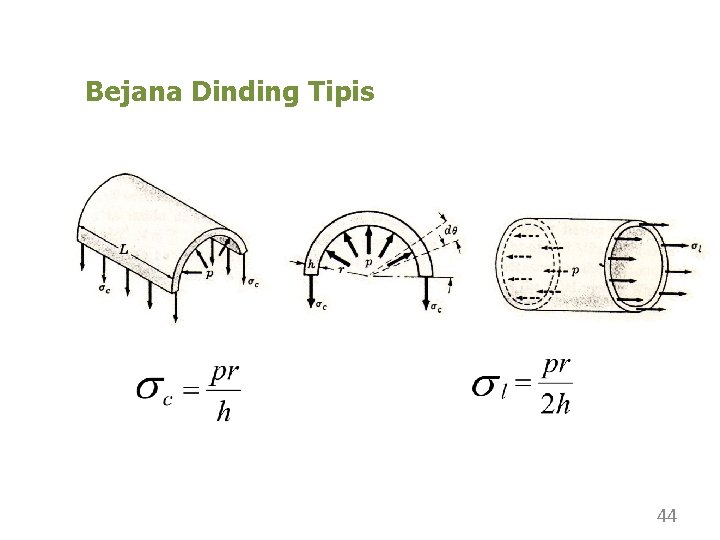
Bejana Dinding Tipis 44