TEORI DUALITAS Pengertian Dualitas Konsep dualitas menjelaskan sebuah

TEORI DUALITAS

Pengertian Dualitas • Konsep dualitas menjelaskan sebuah kasus PL berhubungan dengan kasus PL lainnya. • Setiap PL terdiri dari 2 bentuk: - Primal : bentuk pertama PL - Dual : bentuk kedua PL yang berkaitan dengan bentuk pertama PL (primal) • Menyelesaikan masalah primal sekaligus akan menyelesaikan kasus dual dan sebaliknya

Contoh Berikut ini diberikan tabel jumlah mineral dan vitamin yang terdapat pada dua jenis makanan tiruan yaitu daging dan sayuran perunit, serta harganya. Kandungan Makanan Tiruan Daging Sayuran Kebutuhan minimum per hari Mineral 2 4 40 Vitamin 3 2 50 Harga Per Unit 3 2, 5 Masalah adalah menentukan biaya pembelian sejumlah daging dan sayuran sehingga kebutuhan minimum akan mineral dan vitamin BUATLAH MODELNYA ! terpenuhi

Misalkan banyaknya daging yang dibeli x 1 unit banyaknya sayuran yang dibeli x 2 unit Minimumkan z = 3 x 1+2, 5 x 2 Dengan kendala: 2 x 1+4 x 2 ≥ 40 3 x 1+2 x 2 ≥ 50 x 1, x 2 ≥ 0

• Pemasok harus menetapkan harga jual vitamin/unit sebesar y 1 dan harga jual mineral/unit sebesar y 2 agar menghasilkan harga jual daging dan sayuran tiruan yang tidak melebihi harga pasar. Maka model dualnya adalah Maksimumkan w = 40 y 1+50 y 2 Dengan kendala : 2 y 1+3 y 2 ≤ 3 4 y 1+2 y 2 ≤ 2, 5 y 1, y 2 ≥ 0

Minimumkan z = 3 x 1+2, 5 x 2 kendala: 2 x 1+4 x 2 ≥ 40 y 1 3 x 1+2 x 2 ≥ 50 y 2 x 1, x 2 ≥ 0 Dalam Maksimumkan w =40 y 1+50 y 2 kendala : 2 y 1+3 y 2 ≤ 3 4 y 1+2 y 2 ≤ 2, 5 y 1, y 2 ≥ 0 t Primal Dual Kendala i Variabel i Fungsi Tujuan Nilai Kanan

Kasus PL yang Normal Primal Dual Maksimumkan z=c 1 x 1+c 2 x 2+. . . +cnxn Kendala a 11 x 1 + a 12 x 2 +. . . + a 1 nxn ≤ b 1 a 21 x 1 + a 22 x 2 +. . . + a 2 nxn ≤ b 2 ⁞ am 1 x 1 + am 2 x 2 +. . . + amnxn ≤ bm x 1, x 2 , . . . , xn ≥ 0 Minimumkan w=b 1 y 1+b 2 y 2+. . . +bmym Kendala a 11 y 1 + a 21 y 2 +. . . + am 1 ym ≥ c 1 a 12 y 1 + a 22 y 2 +. . . + am 2 ym ≥ c 2 ⁞ a 1 ny 1 + a 2 ny 2 +. . . + amnym ≥ cn y 1, y 2 , . . . , ym ≥ 0 Minimumkan z=c 1 x 1+c 2 x 2+. . . +cnxn Kendala a 11 x 1 + a 12 x 2 +. . . + a 1 nxn ≥ b 1 a 21 x 1 + a 22 x 2 +. . . + a 2 nxn≥b 2 ⁞ am 1 x 1 + am 2 x 2 +. . . + amnxn ≥ bm x 1, x 2 , . . . , xn ≥ 0 Maksimumkan w=b 1 y 1+b 2 y 2+. . . +bmym Kendala a 11 y 1 + a 21 y 2 +. . . + am 1 ym ≤c 1 a 12 y 1 + a 22 y 2 +. . . + am 2 ym≤c 2 ⁞ a 1 ny 1 + a 2 ny 2 +. . . + amnym ≤ cn y 1, y 2 , . . . , ym ≥ 0

Hubungan Primal dan Dual • Koefisien fungsi tujuan di masalah primal menjadi konstanta ruas kanan dari fungsi kendala pada masalah dual • Tanda pertidaksamaan kendala dibalik • Tujuan minimasi di primal diubah menjadi maksimasi di dual dan sebaliknya • Setiap kolom koefisien di primal adalah satu koefisien kendala di dual • Bentuk dual dari dual adalah primal

Buatlah Dual dari permasalahan Primal berikut ini Maksimumkan z = 2 x 1 + 3 x 2 + 4 x 3 Kendala x 1 + 2 x 2 + 5 x 3 ≤ 20 3 x 1 + x 2 + 4 x 3 ≤ 12 x 1, x 2 , x 3 ≥ 0 Minimumkan z = x 1 + 2 x 2 + 2 x 3 Kendala 2 x 1 + x 2 + 5 x 3 ≥ 40 x 1 + 4 x 2+ 2 x 3 ≥ 32 x 1, x 2 , x 3 ≥ 0

Persamaan PL yang Tidak Normal • Jika kasus minimasi ada kendala dengan tanda ‘=‘ dan ‘≤’ • Jika kasus maksimasi ada kendala dengan tanda ‘=‘ dan ‘≥’

Langkah mengubah persoalan maksimasi/minimasi menjadi persoalan normal • Kalikan setiap kendala ‘≥’ (untuk maksimasi) atau ‘≤’ (untuk minimasi) dengan bilangan -1. • Ganti setiap kendala ‘=‘ dengan dua ketidaksamaan (‘≥’ dan ‘≤’). • Ganti setiap variabel xj tak terbatas menjadi xj = xj‘-xj’’ dimana xj‘ ≥ 0, xj’’ ≥ 0.

Hal yang Harus diperhatikan dalam Membangun Dual Persamaan PL yang Tidak Normal 1. Persoalan : – Maksimasi : Jika kendala primal ke-i bertanda ‘≥’, maka variabel dual yang berkorespondensi dengan kendala tersebut akan memenuhi yi ≤ 0. – Minimasi : Jika kendala primal ke-i bertanda ‘≤’, maka variabel dual yang berkorespondensi dengan kendala tersebut akan memenuhi yi ≤ 0.

Hal yang Harus diperhatikan dalam Membangun Dual Persamaan PL yang Tidak Normal 2. Jika kendala primal ke-i bertanda ‘=‘, maka variabel dual yang berkorespondensi dengan kendala tersebut akan tidak terbatas dalam tanda. 3. Jika variabel primal ke-i tidak terbatas dalam tanda, maka kendala dual ke-i akan bertanda ‘=‘.

Contoh Primal : Maksimumkan z = x 1 + 2 x 2 – 3 x 3 + 4 x 4 Kendala x 1 + 2 x 2 + 2 x 3 – 3 x 4 2 x 1 + x 2 – 3 x 3 + 2 x 4 x 1 , x 2 , x 3 , x 4 ≥ 0 ≤ 25 = 15 Standar Primal : Maksimumkan z = x 1 + 2 x 2 – 3 x 3 + 4 x 4 + 0 S 1 – MR 2 Kendala x 1 + 2 x 2 + 2 x 3 – 3 x 4 + S 1 = 25 y 1 y 2 2 x 1 + x 2 – 3 x 3 + 2 x 4 + R 2 = 15 x 1 , x 2 , x 3 , x 4 , S 1 , R 2 ≥ 0

Dual : Minimumkan w = 25 y 1 + 15 y 2 Kendala y 1 + 2 y 2 ≥ 1 2 y 1 + y 2 ≥ 2 2 y 1 – 3 y 2 ≥ – 3 y 1 + 2 y 2 ≥ 4 y 1 + 0 y 2 ≥ 0 y 2 = 0 y 1 ≥ 0 y 2 tidak terbatas dalam tanda • Catatan : – Karena y 2 tidak terbatas dalam tanda, maka y 2 memiliki dua harga yaitu y 2 = (y 2’ –y 2’’)

Standar Dual : Minimumkan w = 25 y 1+15(y 2’ –y 2’’)+MR 1+MR 2+MR 3+MR 4 Kendala y 1 + 2(y 2’ –y 2’’) – S 1 +R 1 = 1 2 y 1 + (y 2’ –y 2’’) – S 2 +R 2 = 2 2 y 1 – 3(y 2’ –y 2’’) – S 3 +R 3 = – 3 y 1 + 2(y 2’ –y 2’’) – S 4 +R 4 = 4 y 1 , y 2’’, S 1 , S 2 , S 3 , S 4 , R 1 , R 2 , R 3 , R 4 ≥ 0

Buatlah bentuk standar dari persoalan primal berikut ini, tentukan bentuk dual dan dual standarnya Maksimumkan z = 5 x 1 + 12 x 2 + 4 x 3 Kendala x 1 + 2 x 2 + x 3 ≤ 10 2 x 1 - x 2 +3 x 3 = 8 x 1 , x 2 , x 3 ≥ 0 Bentuk Primal Standar Maksimumkan z = 5 x 1 +12 x 2 + 4 x 3 + 0 S 1 - MR 3 Kendala x 1 + 2 x 2 + x 3 + S 1 = 10 2 x 1 x 2+3 x 3 +R 3 = 8 x 1 , x 2 , x 3, S 1, R 3 ≥ 0

1 Primal iterasi 0 1 2 3 4 basis x 1 x 2 x 3 S 1 R 1 Solusi z -2 M-5 M-12 -3 M-4 0 0 -8 M S 1 1 2 1 1 0 10 R 1 2 -1 3 0 1 8 z -7/3 -40/3 0 0 4/3+M 32/3 S 1 1/3 7/3 0 1 -1/3 22/3 x 3 2/3 -1/3 1 0 1/3 8/3 z -3/7 0 0 40/7 M-4/7 368/7 x 2 1/7 1 0 3/7 -1/7 22/7 x 3 5/7 0 1 1/7 26/7 z 0 0 3/5 29/5 -2/5+M 544/5 x 2 0 1 1/5 2/5 -1/5 12/5 x 1 1 0 7/5 1/5 26/5

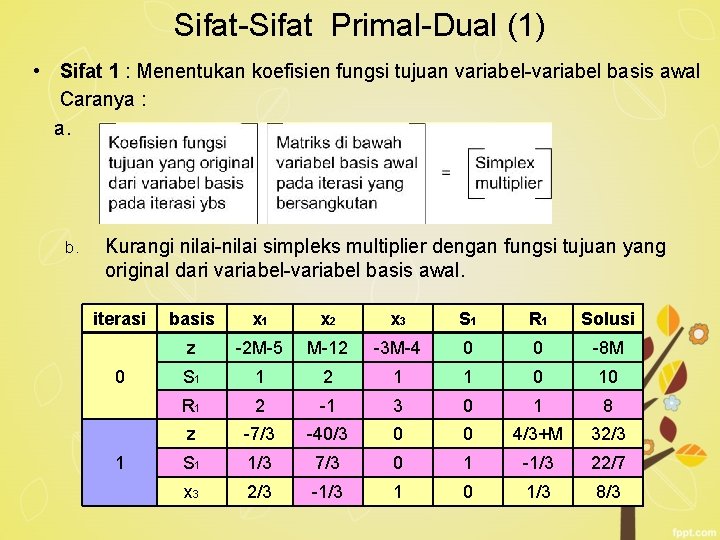
Sifat-Sifat Primal-Dual (1) • Sifat 1 : Menentukan koefisien fungsi tujuan variabel-variabel basis awal Caranya : a. b. Kurangi nilai-nilai simpleks multiplier dengan fungsi tujuan yang original dari variabel-variabel basis awal. iterasi 0 1 basis x 1 x 2 x 3 S 1 R 1 Solusi z -2 M-5 M-12 -3 M-4 0 0 -8 M S 1 1 2 1 1 0 10 R 1 2 -1 3 0 1 8 z -7/3 -40/3 0 0 4/3+M 32/3 S 1 1/3 7/3 0 1 -1/3 22/7 x 3 2/3 -1/3 1 0 1/3 8/3

• Yang menjadi basis pada iterasi 1 adalah S 1 dan x 3, koefisien fungsi tujuan pada iterasi awal adalah 0 dan 4. S 1 dan R 1 adalah basis pada iterasi awal maka matriks dibawah variabel S 1 dan R 1 pada iterasi 1 adalah Cek untuk iterasi 2 dan 3 • Sehingga simplex multipliers-nya Tabel • Kurangi simpleks multipliers dengan koefisien fungsi tujuan dari basis – basis iterasi awal yaitu S 1 dan R 1 , nilainya 0 dan –M sehingga diperoleh Adalah koefisien fungsi tujuan S 1 dan R 1 pada iterasi 1.

Sifat-Sifat Primal-Dual (2) � Sifat 2 : Menentukan koefisien fungsi tujuan variabel- variabel non basis awal Cek untuk iterasi 2 dan 3 Caranya : Kalikan vektor baris simpleks multiplier pada iterasi yang bersangkutan dengan matriks koefisien kendala pada iterasi awal lalu dikurangkan dengan vektor baris koefisien fungsi tujuan variabel nonbasis pada iterasi awal. Dari contoh diiterasi pertama diperoleh koefisien x 1 , x 2 , x 3 Tabel

Sifat-Sifat Primal-Dual (3) • Sifat 3 : Menentukan nilai ruas kanan (solusi) dari variabel-variabel basis Caranya : � Sifat 4 : Menentukan koefisien kendala/pembatas Caranya :

Dari contoh sifat 3 dapat digunakan misalkan untuk iterasi 1 awal maka iterasi 1 Cek untuk iterasi 2 dan 3 Tabel

Dari contoh sifat 4 dapat dihitung koefisien kendala pada iterasi 1, matriks dibawah basis awal pada iterasi 1 adalah Tabel Dan matriks koefisien kendala pada iterasi awal adalah sehingga Cek untuk iterasi 2 dan 3

Latihan Primal : F. Tujuan : Maks Z = 4 x 1 + 6 x 2 + 2 x 3 F. Pembatas : 4 x 1 – 4 x 2 ≤ 5 – x 1 + 6 x 2 ≤ 5 – x 1 + x 2 + x 3 ≤ 5 x 1 , x 2 , x 3 ≥ 0 Salah satu iterasi dari persoalan diatas adalah Basis x 1 x 2 x 3 S 1 S 2 S 3 Solusi z d e f a b c t x 1 j m p 6/20 4/20 0 g x 2 k n q 1/20 4/20 0 h S 3 l o r 5/20 0 1 i Tentukan nilai a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t