Teori Bahasa dan Automata BAHASA REGULAR Ekspresi Regular

Teori Bahasa dan Automata BAHASA REGULAR & Ekspresi Regular By Kustanto Materi ke 4 B otomata 10/27/2021 1

PENDAHULUAN Bahasa regular adalah penyusun ekspresi reguler (ER) Ekspresi reguler terdiri dari kombinasi simbol-simbol atomik menggunakan 3 operasi yaitu : – katenasi, – alternasi, dan – repetisi /closure Pada kasus scanner, simbol-simbol atomik adalah karakter-karakter di dalam program sumber. Dua buah ekspresi regular adalah ekuivalen jika keduanya menyatakan bahasa yang sama Materi ke 4 B otomata 10/27/2021 2

Operasi Regular - alternasi Alternasi membolehkan pilihan dari beberapa pilihan dan biasanya disajikan dengan operator ‘|’ – E. g. <digit> : : = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 » contoh yang menggunakan juga operator persamaan (equivalency) Bentuk tulisan cepat tertentu juga biasanya digunakan dengan alternasi (khususnya ellips) – E. g. <letter> : : = a | b | … | z | A | B | … | Z » Can use the ellipses (“…”) when a sequence is well defined Materi ke 4 B otomata 10/27/2021 3

Operasi Regular - repetisi Terakhir, repetisi membolehkan ekspresi dari kontruksi yang diulang beberapa kali Terdapat 2 operator yang digunakan yaitu superscript ‘+’ dan superscript ‘*’ – E. g. <word> : : = <letter>+ » this implies a word consists of one or more letters (* would imply zero or more letters and a word must have at least one letter so we use +) Materi ke 4 B otomata 10/27/2021 4

• Ekspresi Regular Ekuivalensi Non Deterministic Finite Automata ke Deterministic Finite Automata • Materi ke 4 B otomata 10/27/2021 5

Ekspresi Regular – Introduction Sebuah bahasa dinyatakan regular jika terdapat finite state automata yang dapat menerimanya Bahasa-bahasa yang diterima oleh suatu finite state automata bisa dinyatakan secara sederhana dengan ekspresi regular (regular expression) ER. Memberikan suatu pola (pattern) atau template untuk string dari suatu bahasa String yang menyusun suatu bahasa regular akan cocok (match) dengan pola bahasa itu Penerapan ekspresi regular yang tampak misalnya string search pada suatu file, biasanya fasilitas ini ada pada text editor. Materi ke 4 B otomata 10/27/2021 6
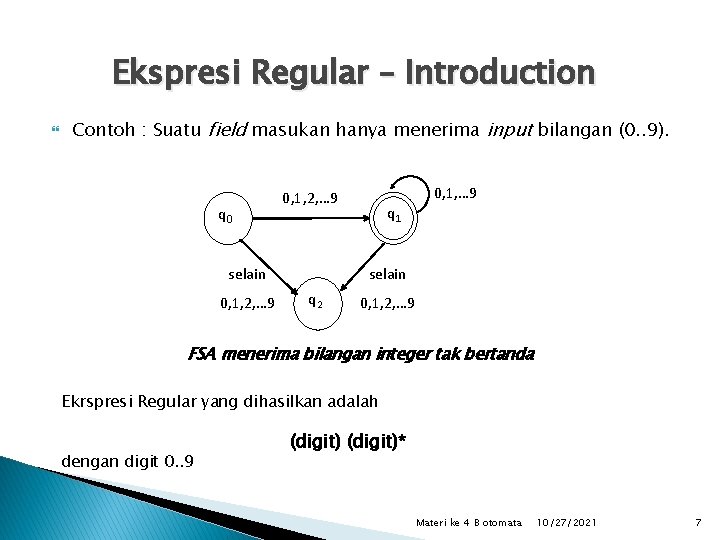
Ekspresi Regular – Introduction Contoh : Suatu field masukan hanya menerima input bilangan (0. . 9). q 0 selain 0, 1, 2, … 9 q 1 selain q 2 0, 1, 2, … 9 FSA menerima bilangan integer tak bertanda Ekrspresi Regular yang dihasilkan adalah dengan digit 0. . 9 (digit)* Materi ke 4 B otomata 10/27/2021 7

Ekspresi Regular – Introduction ER juga dapat diaplikasikan untuk melakukan analisis leksikal dalam sebuah kompilator. Yaitu mengidentifikasikan unit-unit leksikal (token) yang dikenal dalam program. Token-token pada suatu bahasa pemrograman kebanyakan tanpa kecuali dinyatakan sebagai sebuah ER. Contoh: Suatu identifier baik huruf besar atau huruf kecil yang kemudian diikuti huruf atau digit, dengan tanpa pembatasan jumlah panjang bisa dinyatakan sebagai: (huruf)(huruf+digit)* q 0 huruf q 1 huruf atau digit Materi ke 4 B otomata 10/27/2021 8

Notasi ER Terdapat 5 notasi dalam ER yaitu: ‘*’ , ‘+’ , ‘. ’ * (karakter asterisk), berarti bisa tidak muncul, bisa juga muncul berhingga kali (0 -n) + (pada posisi superscript/ diatas) berarti minimal muncul satu kali (1 -n) + atau berarti union . (titik) berarti konkatensi, biasanya titik bisa dihilangkan, misal ab bermakna seperti a. b Materi ke 4 B otomata 10/27/2021 9

Notasi ER - Contoh ER: ab*cc Contoh string: abcc, abbbcc, abbbbcc, acc, (b bisa tidak muncul atau muncul sejumlah berhingga kali) ER: 010* Contoh string : 01, 0100, 01000 (jumlah 0 diujung bisa tidak muncul, bisa muncul berhingga kali) ER: a*d Contoh string : d, aad, aaad ER: a+d Contoh string: ad, aaad --- (a minimal muncul sekali) Materi ke 4 B otomata 10/27/2021 10

Notasi ER -Contoh ER: a* b* (ingat ‘ ’ berarti atau) Contoh string : a, b, aa, bb, aaa, bbb, aaaa, bbbb ER: (a b) --- Contoh string: a, b ER: (a b)* Contoh string : a, b, ab, ba, abb, bba, aaaa, bbbb (string yang memuat a atau b) ---- * perhatikan : notasi ‘ ’ kadang dituliskan juga sebagai ‘+’ -- ER: 01*+0 Contoh string: 0, 011, 01111, (string yang berawalan dengan 0, dan selanjutnya boleh diikuti deretan 1) Materi ke 4 B otomata 10/27/2021 11
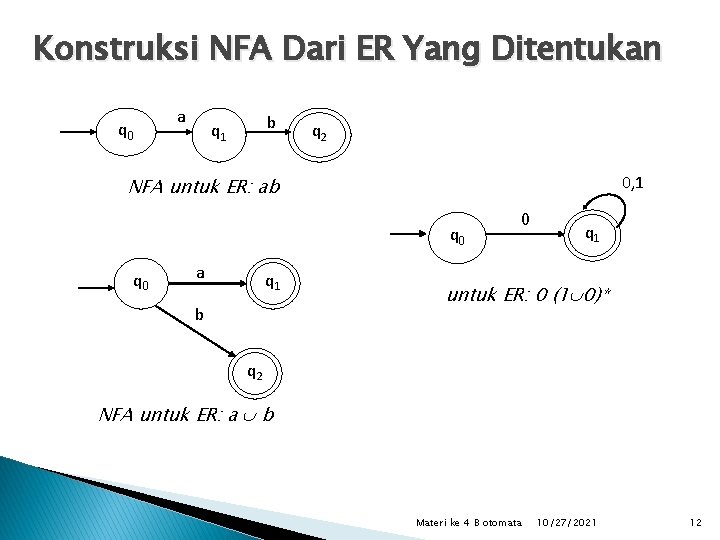
Konstruksi NFA Dari ER Yang Ditentukan q 0 a b q 1 q 2 0, 1 NFA untuk ER: ab q 0 a q 1 b 0 q 1 untuk ER: 0 (1 0)* q 2 NFA untuk ER: a b Materi ke 4 B otomata 10/27/2021 12

Ekuivalensi NFA ke DFA � � Dari sebuah mesin Non-deterministic Finite Automata dapat dibuat mesin Deterministic Finite Automata-nya yang ekivalen (bersesuaian) Ekivalen disini artinya mampu menerima bahasa yang sama L(M 1) = L(M 2) 0, 1 0 q 0 0, 1 q 1 0 0, 1 1 q 0 q 1 q 2 Materi ke 4 B otomata 10/27/2021 13

Ekuivalensi NFA ke DFA – Steps Membuat tabel transisi Mulai dari state awal Ikuti transisinya untuk membentuk state-state baru Untuk setiap state yang terbentuk diikuti lagi transisinya sampai ter’cover’ semua Materi ke 4 B otomata 10/27/2021 14
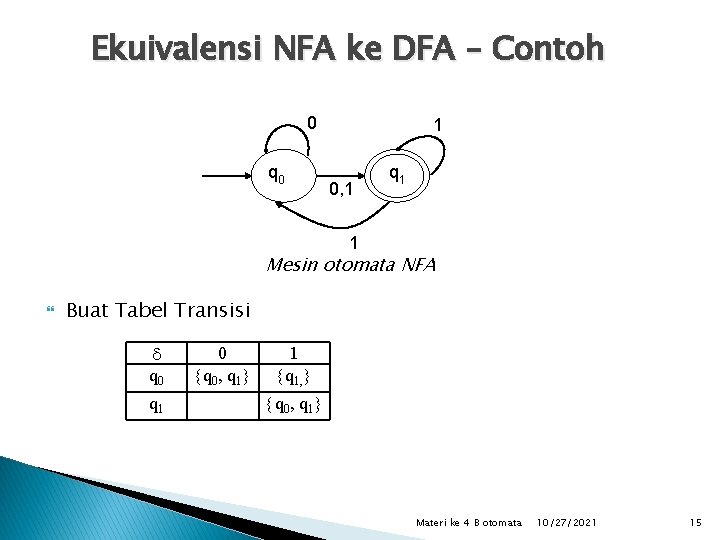
Ekuivalensi NFA ke DFA – Contoh 0 q 0 1 0, 1 q 1 1 Mesin otomata NFA Buat Tabel Transisi q 0 q 1 0 q 0, q 1 1 q 1, q 0, q 1 Materi ke 4 B otomata 10/27/2021 15
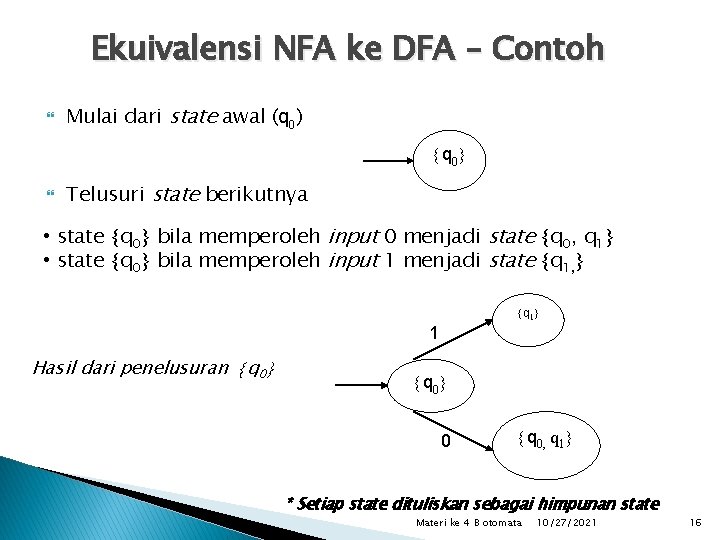
Ekuivalensi NFA ke DFA – Contoh Mulai dari state awal (q 0) q 0 Telusuri state berikutnya • state q 0 bila memperoleh input 0 menjadi state q 0, q 1 • state q 0 bila memperoleh input 1 menjadi state q 1, q 1 1 Hasil dari penelusuran q 0 0 q 0, q 1 * Setiap state dituliskan sebagai himpunan state Materi ke 4 B otomata 10/27/2021 16

Ekuivalensi NFA ke DFA – Contoh Ikuti transisinya untuk membentuk state-state baru • state q 1 bila memperoleh input 0 menjadi state • state q 1 bila memperoleh input 1 menjadi state q 0, q 1 • state q 0, q 1 bila memperoleh input 0 menjadi state q 0, q 1 , ini di peroleh dari (q 0, 0)= q 0, q 1 di gabung dengan (q 1, 0) = , maka hasilnya ( q 0, q 1 , 0) = q 0, q 1 • state q 0, q 1 bila memperoleh input 1 menjadi state q 0, q 1 , ini di peroleh dari (q 0, 1)= q 1 di gabung dengan (q 1, 1) = q 0, q 1 , maka hasilnya ( q 0, q 1 , 1) = q 0, q 1 * Setiap state dituliskan sebagai himpunan state Materi ke 4 B otomata 10/27/2021 17
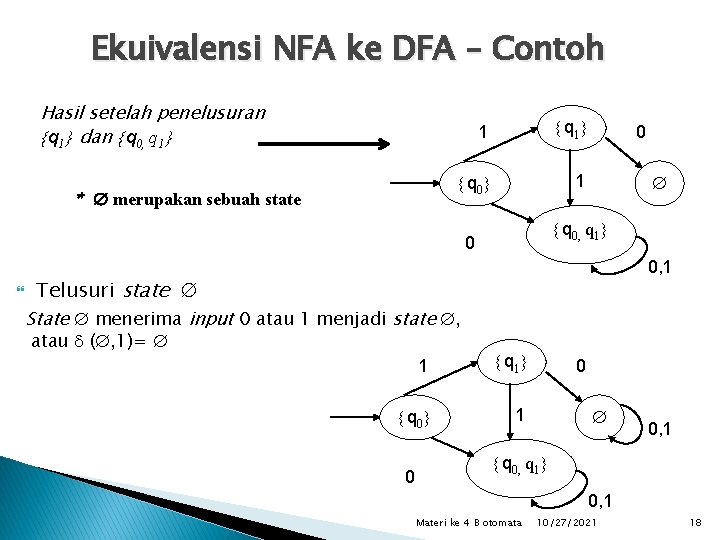
Ekuivalensi NFA ke DFA – Contoh Hasil setelah penelusuran q 1 dan q 0, q 1 * merupakan sebuah state 1 q 0 1 q 0, q 1 0 0 0, 1 Telusuri state State menerima input 0 atau 1 menjadi state , atau ( , 1)= 1 q 0 1 0 0 0, 1 q 0, q 1 0, 1 Materi ke 4 B otomata 10/27/2021 18
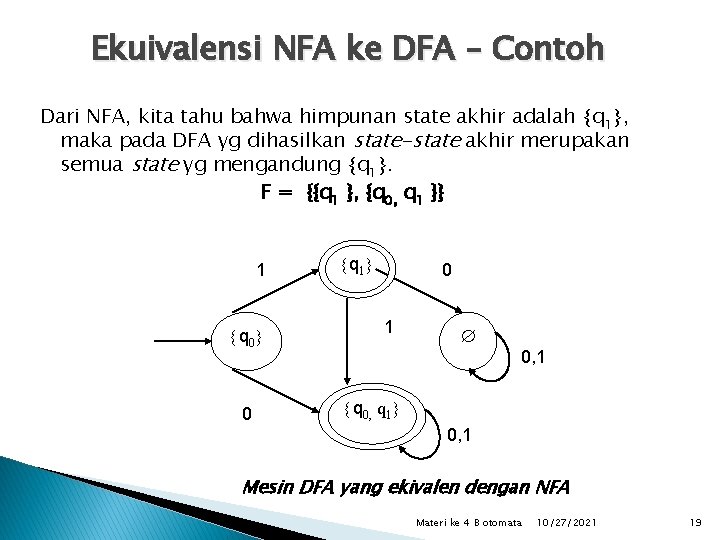
Ekuivalensi NFA ke DFA – Contoh Dari NFA, kita tahu bahwa himpunan state akhir adalah q 1 , maka pada DFA yg dihasilkan state-state akhir merupakan semua state yg mengandung q 1. F = {{q 1 }, {q 0, q 1 }} 1 q 0 0 q 1 0, 1 q 0, q 1 0, 1 Mesin DFA yang ekivalen dengan NFA Materi ke 4 B otomata 10/27/2021 19

Ekuivalensi NFA ke DFA – Contoh Pembuktian : String ‘ 001’ Dari diagram NFA kita bisa lihat bahwa ∂(q 0, 001) dapat diterima oleh NFA tsb. Untuk DFA kita lihat: ∂(q 0, 001) = ∂( q 0, q 1 , 01)= ∂ ( q 0, q 1 , 1)= q 0, q 1 Karena state q 0, q 1 termasuk state akhir, maka berarti string tersebut diterima. Materi ke 4 B otomata 10/27/2021 20

Bahasa Reguler & Ekspresi Reguler End of Session 21 10/27/2021 Ma ter i ke 4 B ot o m ata
- Slides: 21