TEOREMA PYTHAGORAS Standar Kompetensi Dasar Tujuan Pembelajaran Segitiga

TEOREMA PYTHAGORAS Standar Kompetensi Dasar Tujuan Pembelajaran Segitiga Sikusiku Persegi Menemukan Teorema Piythagoras Evaluasi Pembelajaran

Standar kompetensi Menggunakan Teorema Pythagoras dalam pemecahan masalah BALIK LANJUT

Kompetensi Dasar 3. 1 Menggunakan Teorema Pythagoras untuk menentukan panjang sisi-sisi segitiga siku-siku 3. 2 Memecahkan masalah pada bangun datar yang berkaitan dengan Teorema Pythagoras BALIK LANJUT

Tujuan Pembelajaran Setelah mempelajari materi ini, diharapkan siswa mampu: 1. Menemukan teorema pythagoras 2. Menghitung panjang sisi segitiga siku-siku, jika dua sisi lain diketahui 3. Menemukan kebalikan teorema pythagoras LANJUT BALIK

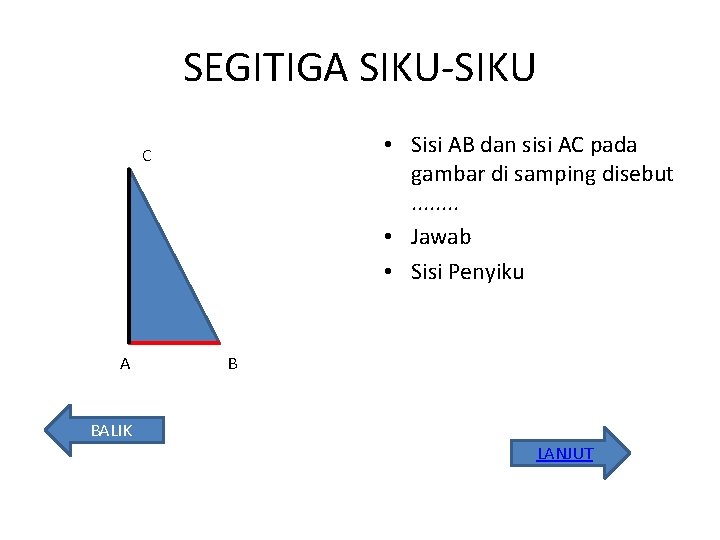
SEGITIGA SIKU-SIKU • Sisi AB dan sisi AC pada gambar di samping disebut. . . . • Jawab • Sisi Penyiku C A B BALIK LANJUT

SEGITIGA SIKU-SIKU • Sisi BC pada gambar di samping disebut. . . . • Jawab • Sisi Miring atau Hipotenusa C A B BALIK LANJUT

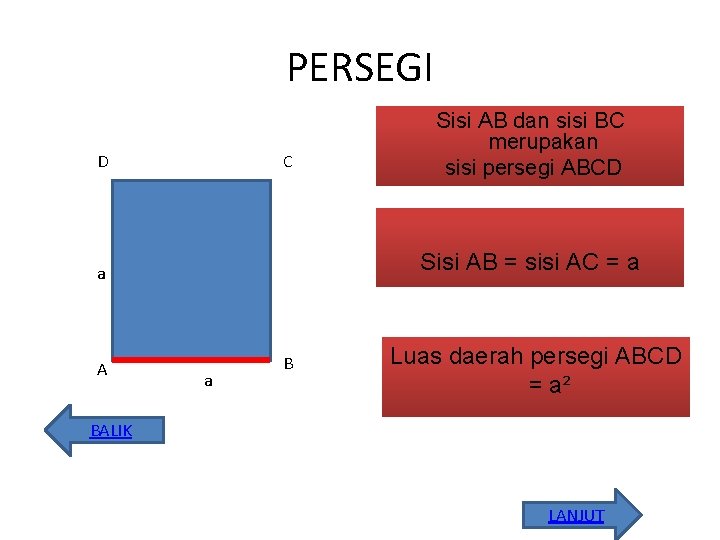
PERSEGI D C Sisi AB = sisi AC = a a A Sisi AB dan sisi BC merupakan sisi persegi ABCD a B Luas daerah persegi ABCD = a² BALIK LANJUT

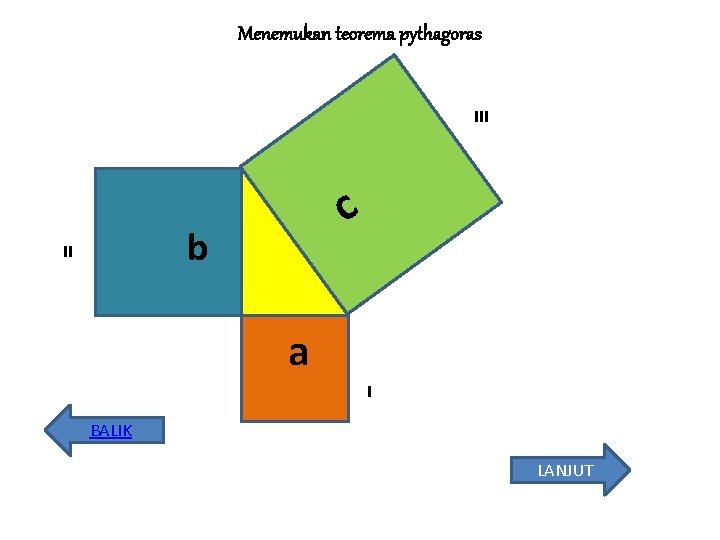
Menemukan teorema pythagoras III c b II a I BALIK LANJUT

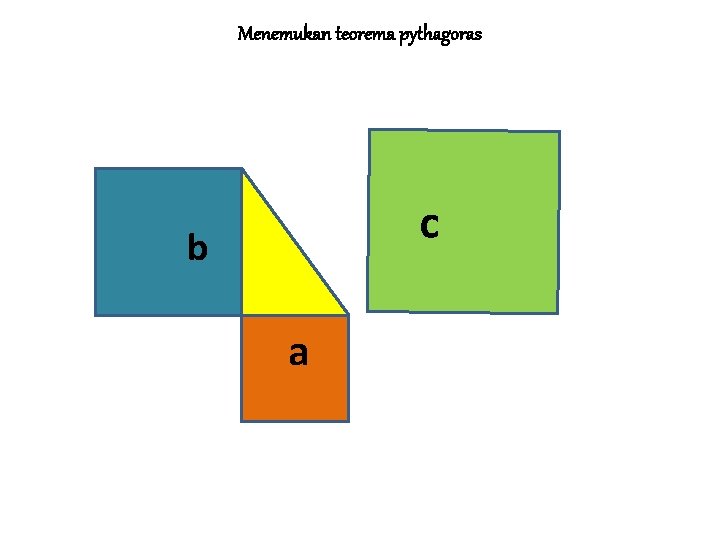
Menemukan teorema pythagoras c b a

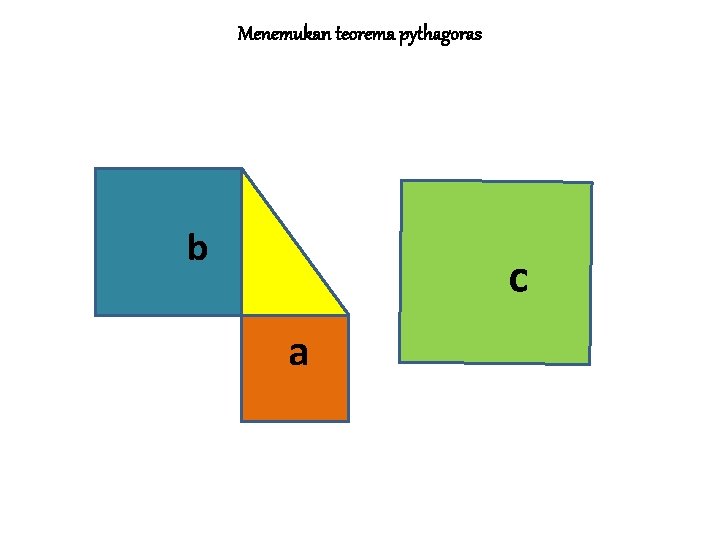
Menemukan teorema pythagoras b c a

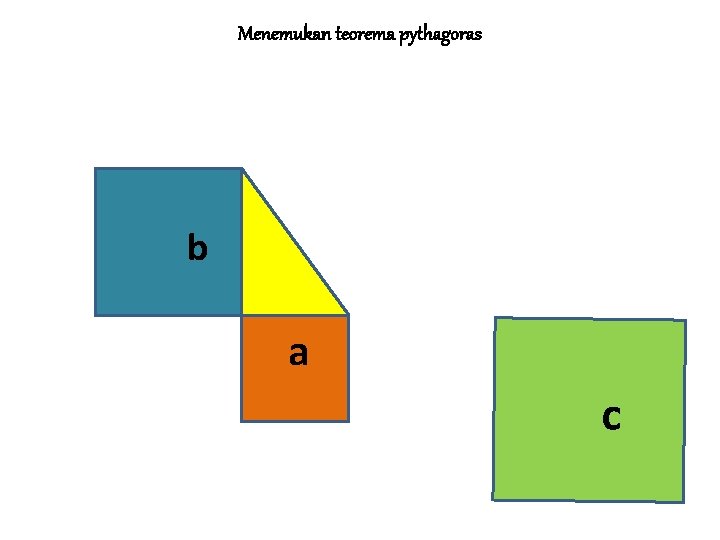
Menemukan teorema pythagoras b a c

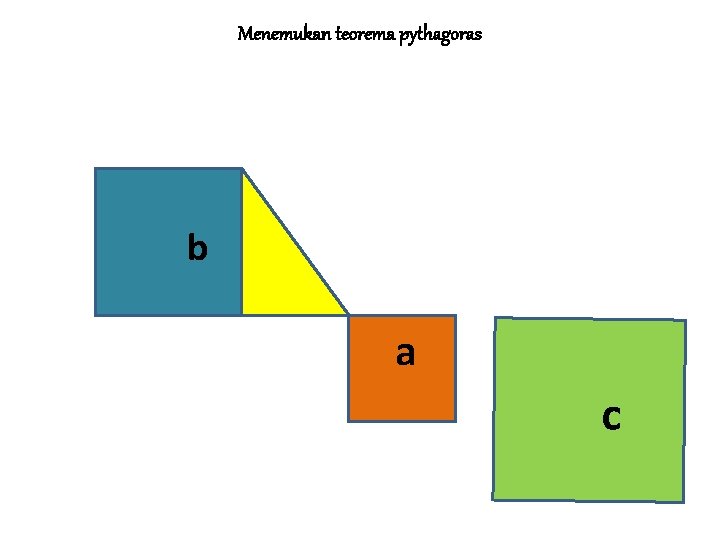
Menemukan teorema pythagoras b a c

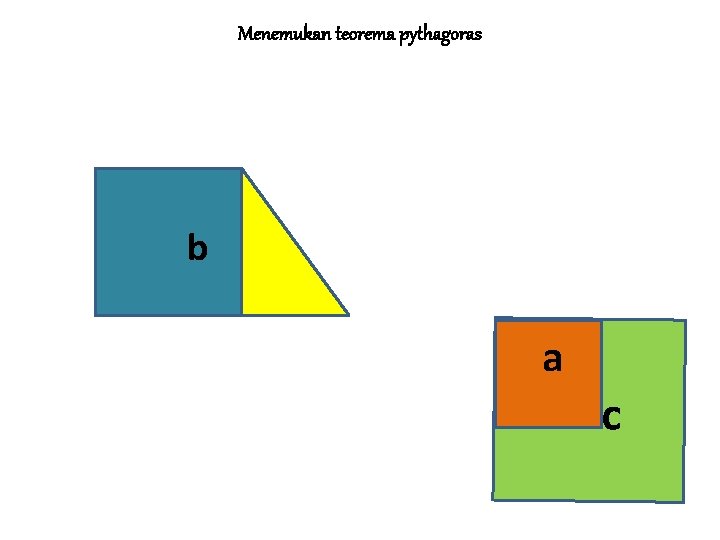
Menemukan teorema pythagoras b a c

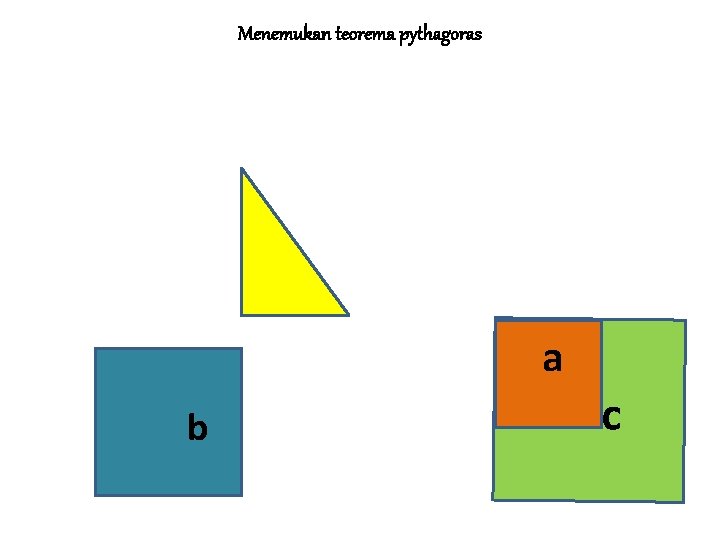
Menemukan teorema pythagoras a b c

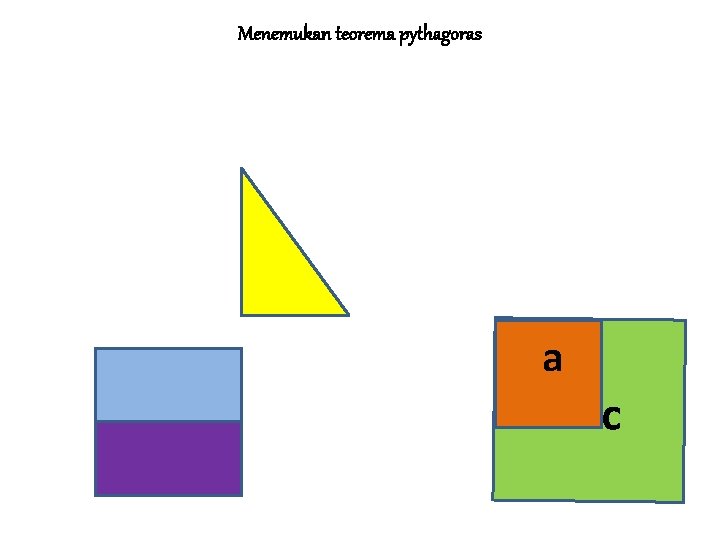
Menemukan teorema pythagoras a b c

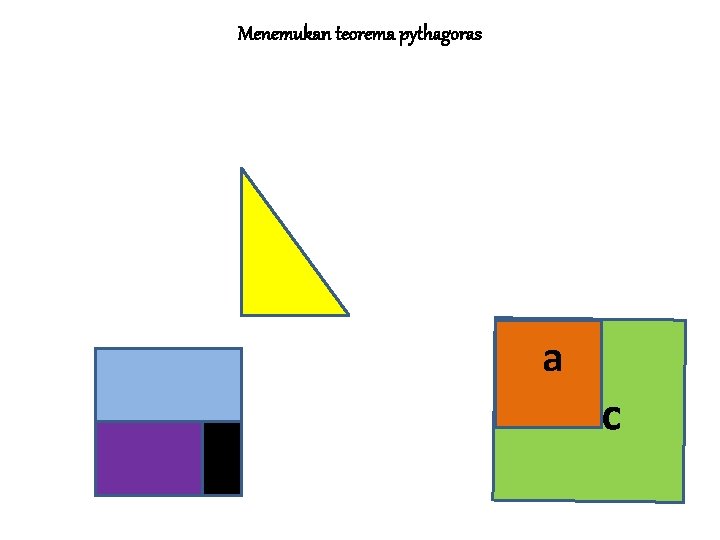
Menemukan teorema pythagoras a b c

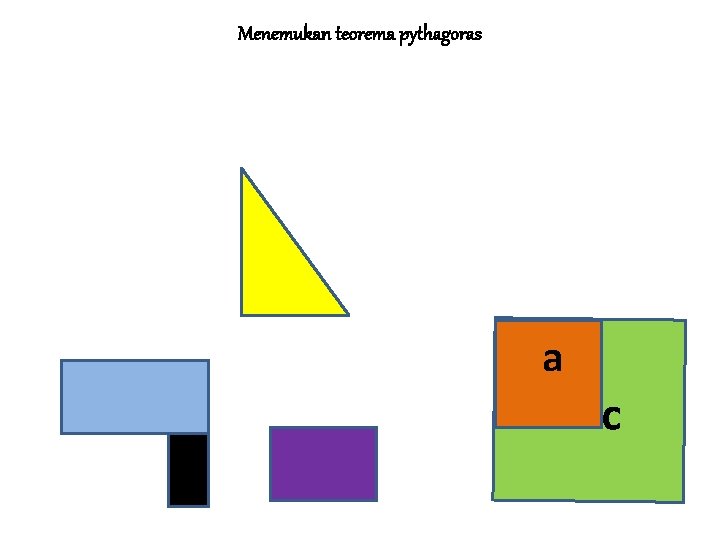
Menemukan teorema pythagoras a c

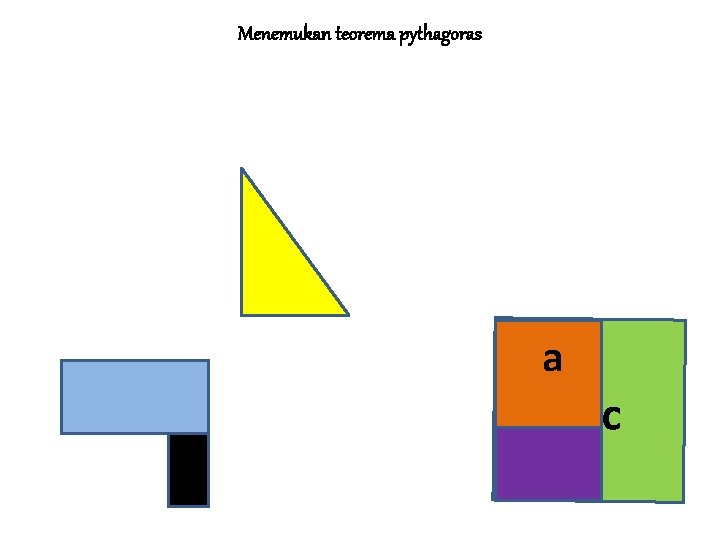
Menemukan teorema pythagoras a c

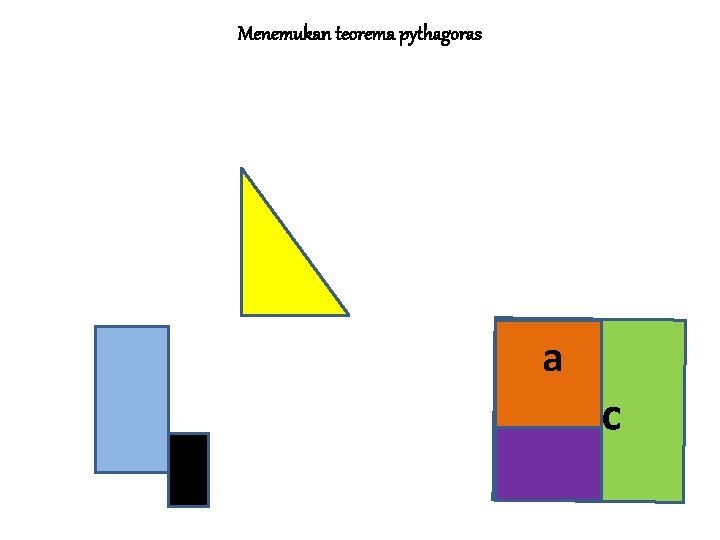
Menemukan teorema pythagoras a c

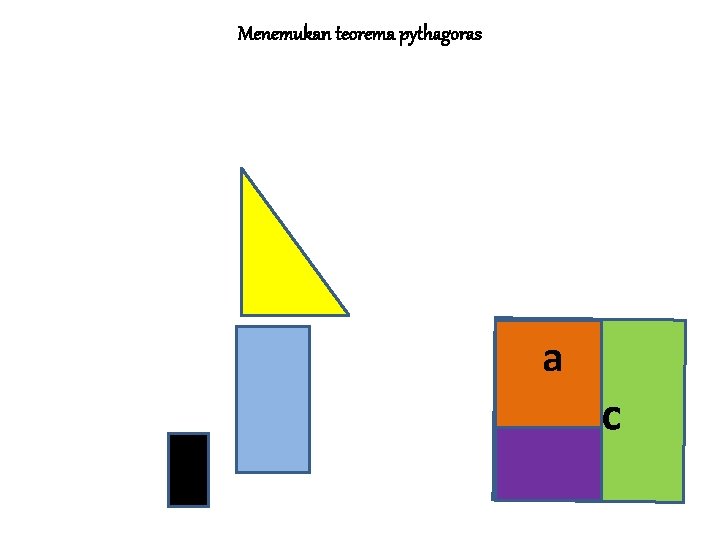
Menemukan teorema pythagoras a c

Menemukan teorema pythagoras a c

Menemukan teorema pythagoras a c

Menemukan teorema pythagoras a c

Menemukan teorema pythagoras a c

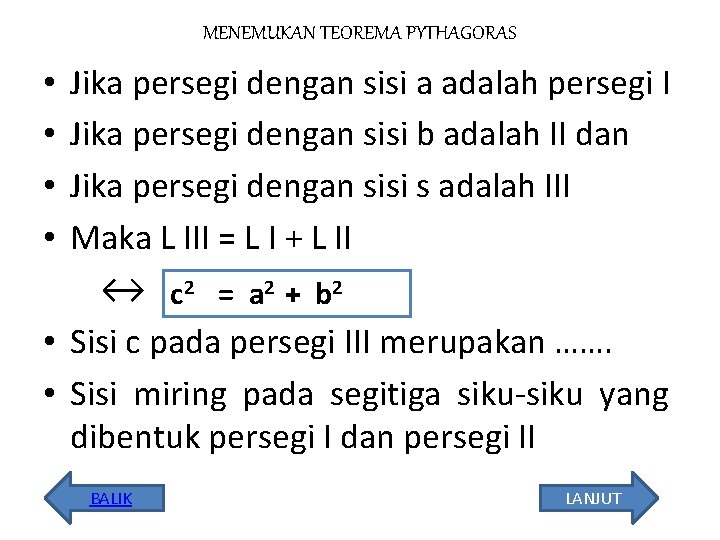
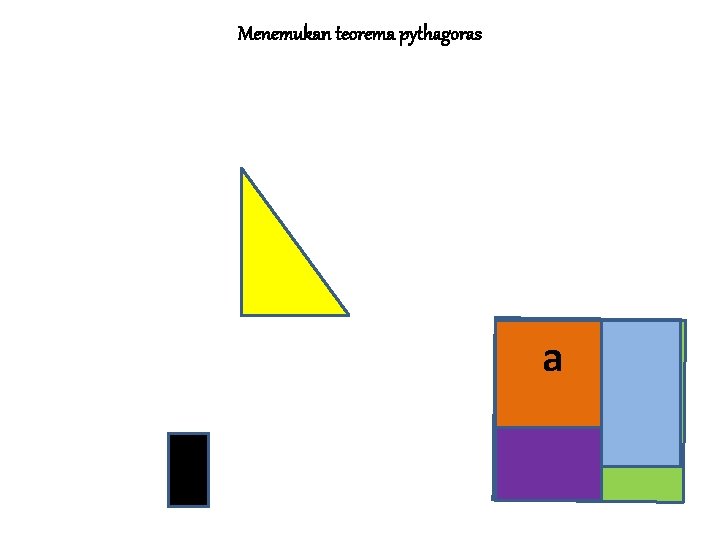
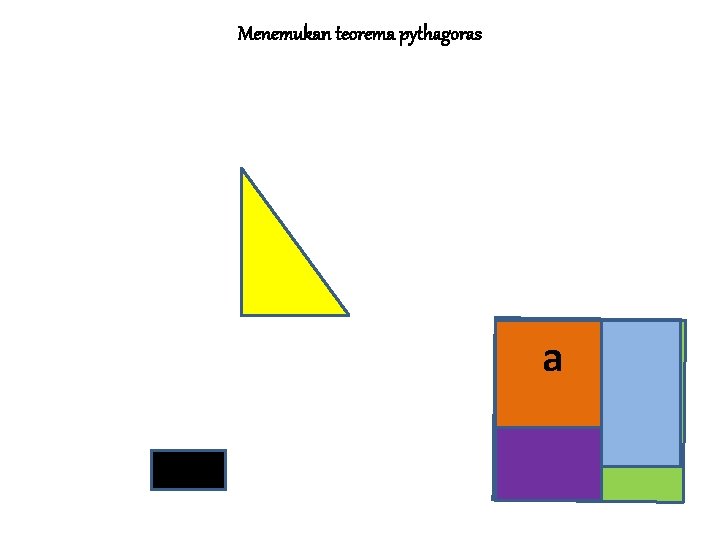
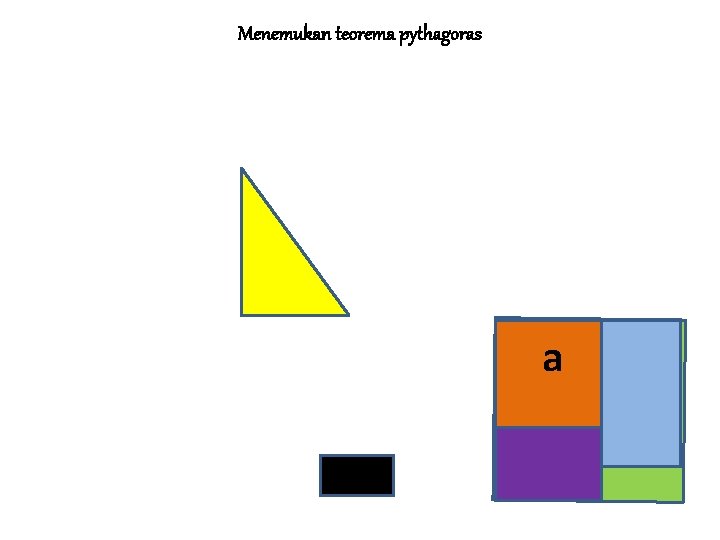
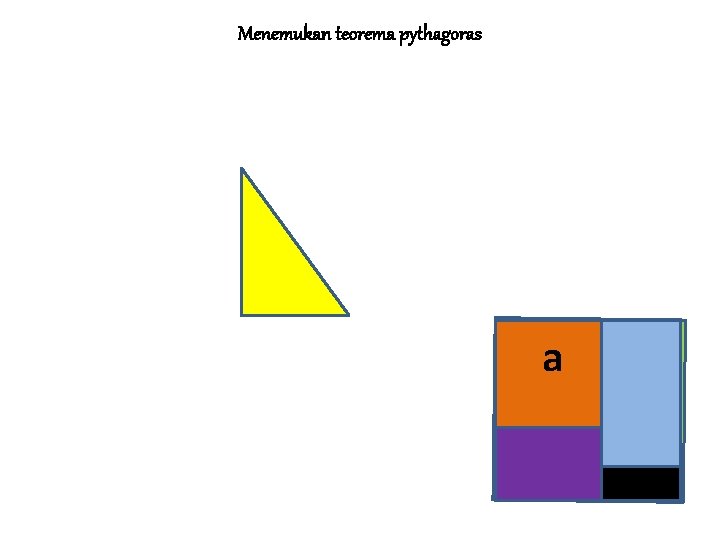
MENEMUKAN TEOREMA PYTHAGORAS Jika persegi dengan sisi a adalah persegi I Jika persegi dengan sisi b adalah II dan Jika persegi dengan sisi s adalah III Maka L III = L I + L II ↔ c 2 = a 2 + b 2 • Sisi c pada persegi III merupakan ……. • Sisi miring pada segitiga siku-siku yang dibentuk persegi I dan persegi II • • BALIK LANJUT

MENEMUKAN TEOREMA PYTHAGORAS • Kesimpulan: • Teorema Pythagoras adalah Kuadrat sisi miring (hipotenusa) pada segitiga siku-siku sama dengan jumlah dari kuadrat masing-masing sisi sikunya BALIK LANJUT

EVALUASI PEMBELAJARAN 1. Pasangan-pasangan bilangan dibawah ini yang dapat membentuk segitiga siku-siku adalah. . . A 1, 2, dan 3 B 3, 4, dan 5 C 6, 7, dan 8 D 9, 10, dan 11 2. Pasangan-pasangan bilangan dibawah ini yang dapat membentuk segitiga siku adalah. . . BALIK LANJUT

Jawaban Anda Salah silahkan coba lagi BALIK LANJUT

Jawaban Anda Benar BALIK LANJUT