TEOREMA BAYES RUMUS DASAR P A dan B

TEOREMA BAYES

RUMUS DASAR : P (A dan B) = P(A). P(B/A) = P (B dan A) = P(B). P(A/B) Peristiwa B bisa terjadi jika salah satu dari n peristiwa yang saling asing A 1, A 2, . . . , An juga terjadi.

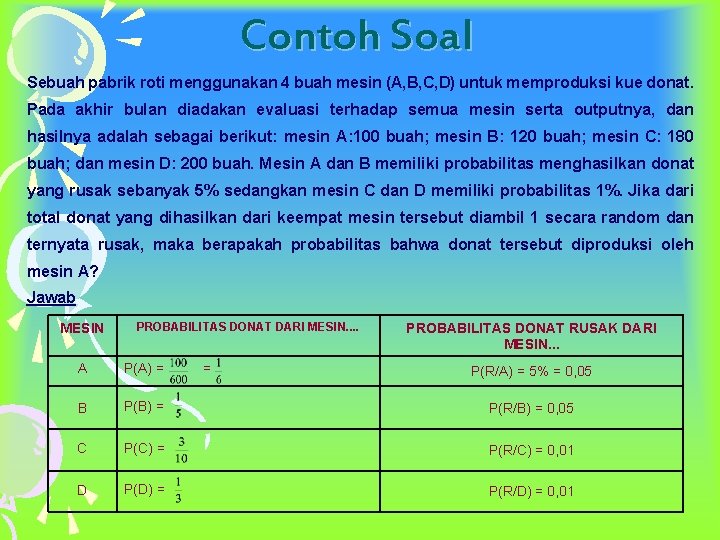
Contoh Soal Sebuah pabrik roti menggunakan 4 buah mesin (A, B, C, D) untuk memproduksi kue donat. Pada akhir bulan diadakan evaluasi terhadap semua mesin serta outputnya, dan hasilnya adalah sebagai berikut: mesin A: 100 buah; mesin B: 120 buah; mesin C: 180 buah; dan mesin D: 200 buah. Mesin A dan B memiliki probabilitas menghasilkan donat yang rusak sebanyak 5% sedangkan mesin C dan D memiliki probabilitas 1%. Jika dari total donat yang dihasilkan dari keempat mesin tersebut diambil 1 secara random dan ternyata rusak, maka berapakah probabilitas bahwa donat tersebut diproduksi oleh mesin A? Jawab MESIN PROBABILITAS DONAT DARI MESIN. . = PROBABILITAS DONAT RUSAK DARI MESIN. . . A P(A) = B P(B) = P(R/B) = 0, 05 C P(C) = P(R/C) = 0, 01 D P(D) = P(R/D) = 0, 01 P(R/A) = 5% = 0, 05

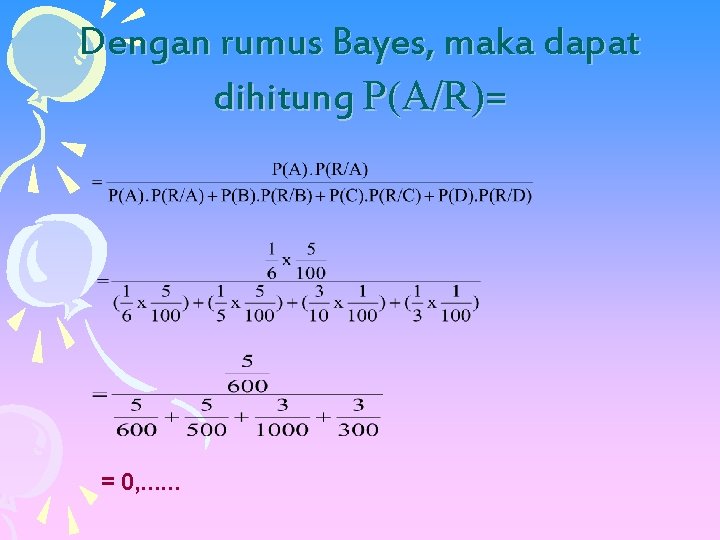
Dengan rumus Bayes, maka dapat dihitung P(A/R)= = 0, . . .

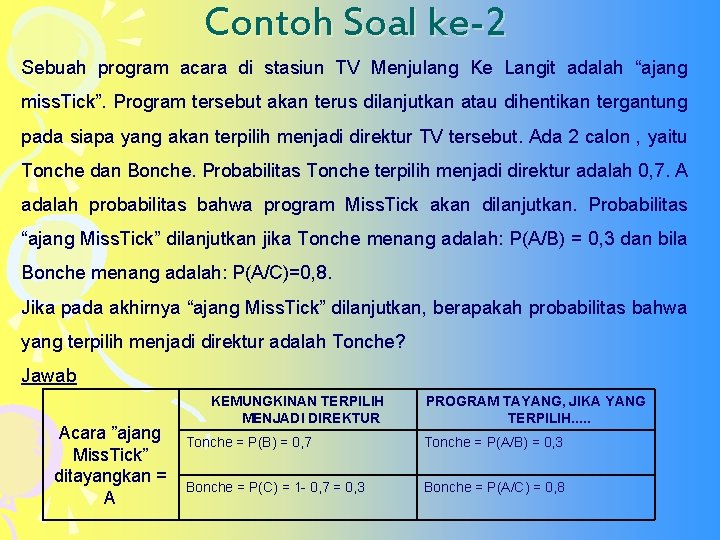
Contoh Soal ke-2 Sebuah program acara di stasiun TV Menjulang Ke Langit adalah “ajang miss. Tick”. Program tersebut akan terus dilanjutkan atau dihentikan tergantung pada siapa yang akan terpilih menjadi direktur TV tersebut. Ada 2 calon , yaitu Tonche dan Bonche. Probabilitas Tonche terpilih menjadi direktur adalah 0, 7. A adalah probabilitas bahwa program Miss. Tick akan dilanjutkan. Probabilitas “ajang Miss. Tick” dilanjutkan jika Tonche menang adalah: P(A/B) = 0, 3 dan bila Bonche menang adalah: P(A/C)=0, 8. Jika pada akhirnya “ajang Miss. Tick” dilanjutkan, berapakah probabilitas bahwa yang terpilih menjadi direktur adalah Tonche? Jawab Acara ”ajang Miss. Tick” ditayangkan = A KEMUNGKINAN TERPILIH MENJADI DIREKTUR PROGRAM TAYANG, JIKA YANG TERPILIH. . . Tonche = P(B) = 0, 7 Tonche = P(A/B) = 0, 3 Bonche = P(C) = 1 - 0, 7 = 0, 3 Bonche = P(A/C) = 0, 8

Dengan rumus Bayes, maka dapat dihitung P(B/A)= = 0, 47

DIAGRAM VENN

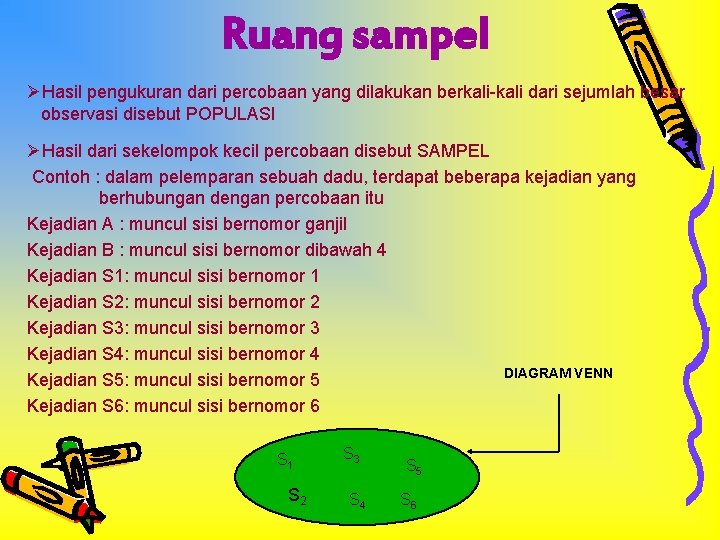
Ruang sampel ØHasil pengukuran dari percobaan yang dilakukan berkali-kali dari sejumlah besar observasi disebut POPULASI ØHasil dari sekelompok kecil percobaan disebut SAMPEL Contoh : dalam pelemparan sebuah dadu, terdapat beberapa kejadian yang berhubungan dengan percobaan itu Kejadian A : muncul sisi bernomor ganjil Kejadian B : muncul sisi bernomor dibawah 4 Kejadian S 1: muncul sisi bernomor 1 Kejadian S 2: muncul sisi bernomor 2 Kejadian S 3: muncul sisi bernomor 3 Kejadian S 4: muncul sisi bernomor 4 DIAGRAM VENN Kejadian S 5: muncul sisi bernomor 5 Kejadian S 6: muncul sisi bernomor 6 S 1 S 2 S 3 S 4 S 5 S 6

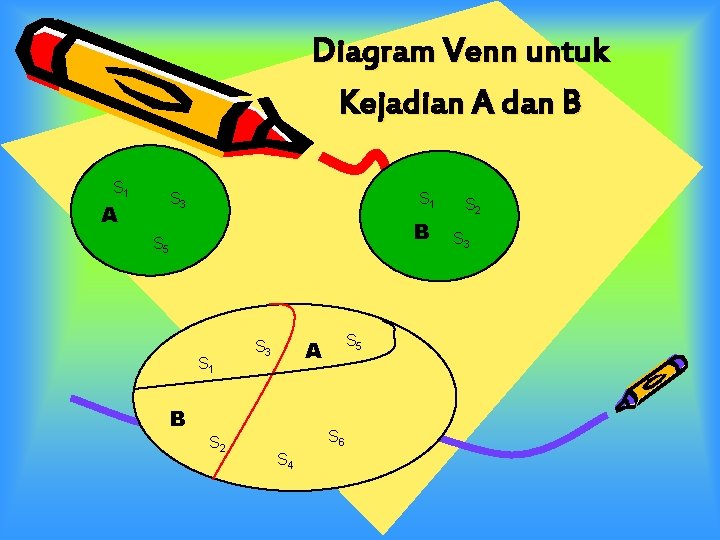
Diagram Venn untuk Kejadian A dan B S 1 S 3 A S 1 B S 5 S 1 B S 2 S 5 A S 3 S 6 S 4 S 2 S 3

Kejadian A = jumlah dari probabilitas dari titik sampel dalam A Kejadian B = jumlah dari probabilitas dari titik sampel dalam B

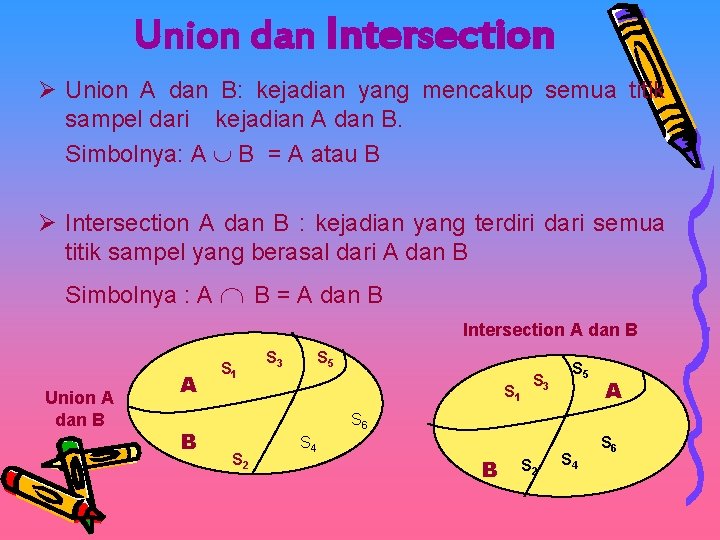
Union dan Intersection Ø Union A dan B: kejadian yang mencakup semua titik sampel dari kejadian A dan B. Simbolnya: A B = A atau B Ø Intersection A dan B : kejadian yang terdiri dari semua titik sampel yang berasal dari A dan B Simbolnya : A B = A dan B Intersection A dan B Union A dan B A B S 1 S 3 S 5 A S 6 S 2 S 4 B S 2 S 4 S 6

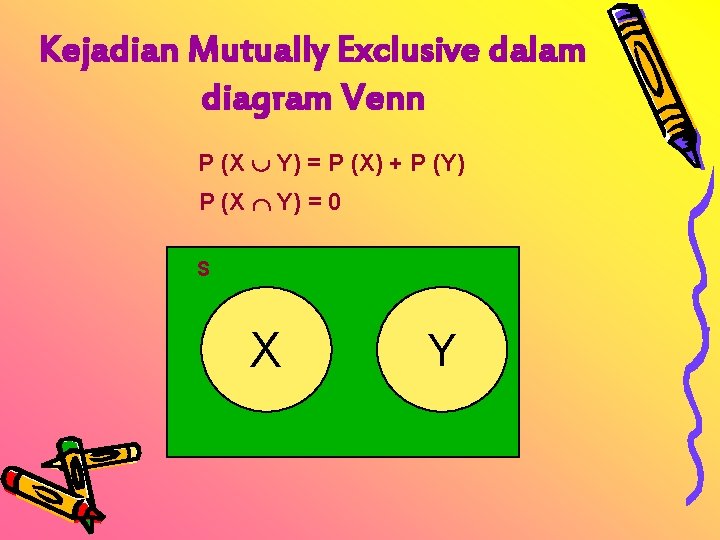
Kejadian Mutually Exclusive dalam diagram Venn P (X Y) = P (X) + P (Y) P (X Y) = 0 S X Y

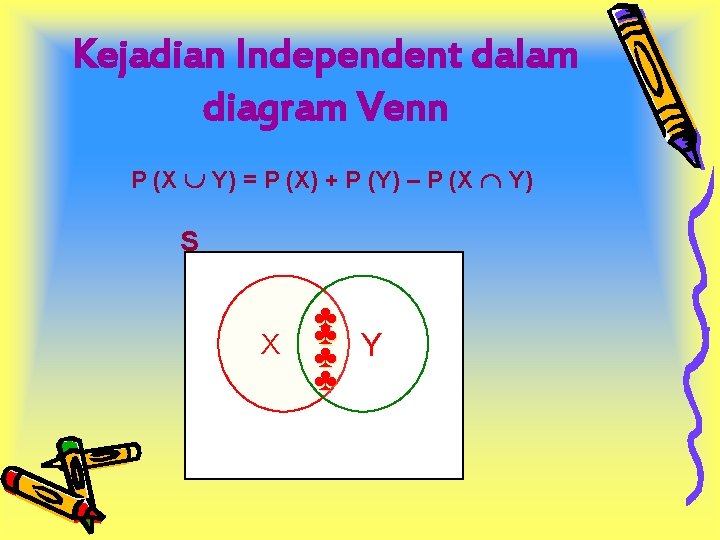
Kejadian Independent dalam diagram Venn P (X Y) = P (X) + P (Y) – P (X Y) S X ♣ ♣ Y ♣ ♣

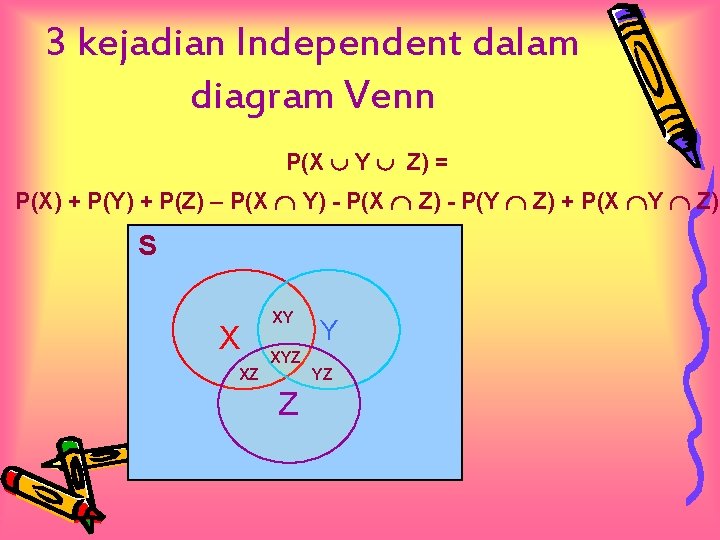
3 kejadian Independent dalam diagram Venn P(X Y Z) = P(X) + P(Y) + P(Z) – P(X Y) - P(X Z) - P(Y Z) + P(X Y Z) S X XZ XY XYZ Z Y YZ

Contoh Soal Dalam sebuah populasi yang terdiri dari pembaca majalah, persentase pembaca majalah Ananda, Bobo, dan Cempaka serta kombinasinya adalah sebagai berikut : Ananda : 7, 3 % Ananda dan Bobo : 6, 7 % Bobo : 17, 9 % Ananda dan Cempaka : 8, 1 % Cempaka: 11, 5 % Bobo dan Cempaka : 2, 7 % Ananda, Bobo, dan Cempaka : 5, 1 % 1. Berapa persen dari populasi yang ternyata membaca paling sedikit 1 dari 3 majalah tersebut? 2. Berapa probabilitas seseorang yang dipilih secara random dari populasi tersebut yang membaca majalah Bobo atau Cempaka? JAWAB 1. P(A B C)=P(A) + P(B) + P(C) – P(A B) - P(A C) - P(B C)+P(A B C) = 7, 3 + 17, 9 + 11, 5 – 6, 7 – 8, 1 – 2, 7 + 5, 1 = 24, 3% = 0, 243 2. P(B C ) = P(B) + P(C)– P(B C) = 17, 9 + 11, 5 -2, 7 = 26, 7 % = 0, 267