Tento projekt je spolufinancovn Evropskm socilnm fondem a

Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem České republiky 1

TEORIE PRAVDĚPODOBNOSTI 2

Teorie pravděpodobnosti n je matematická disciplína, popisující zákonitosti týkající se jevů, které (přinejmenším z hlediska pozorovatele) mohou a nemusí nastat, resp. jejichž výsledná hodnota není předem jistá. n Příkladem může být výsledek hodu kostkou ještě předtím, než hodíme, anebo venkovní teplota zítra v poledne. 3

Základní pojmy Ø Náhodný pokus Ø Náhodný jev Ø Množina všech možných výsledků pokusů 4

Náhodné pokusy (NP) n Pokusy, které při dodržení předepsaných podmínek vedou k různým výsledkům, tzn. výsledky pokusů se od jednoho provedení k druhému mohou měnit. n Pokusy, jejichž výsledky závisí na náhodě. 5

Náhodné pokusy n slosování loterie, tahy sportky, n hody hrací kostkou, mincí, n míchání karet, … 6

Náhodný jev (NJ), ozn. A, B, C, . . . n Jakékoliv tvrzení o výsledku náhodného pokusu, o kterém lze (po provedení pokusu) rozhodnout, zda je pravdivé. n Každý jev, o kterém nejsme schopni předem rozhodnout, zda nastane. n Každý výsledek nebo skupina výsledků náhodného pokusu (NP). 7

Řešený příklad 1: Odlište u následujících situací náhodné pokusy (NP) od náhodných jevů (NJ). n vylosování čísla Ø (NP) n vypěstování rostliny Ø (NP) n vybrání losu s číslem 5 Ø (NJ) n hod kostkou Ø (NP) n vyrobení výrobku 1. jakosti Ø (NJ) n padnutí šestky při hodu kostkou Ø (NJ) n narození chlapce Ø (NJ) 8

Množina možných výsledků pokusů n Předpokládáme, že se jedná o množinu výsledků náhodného pokusu takových, že 1) jsme schopni je všechny předem vyjmenovat (tzn. ve středoškolské matematice vždy konečná), 2) se navzájem vylučují (tzn. nastane-li jeden, nemůže nastat druhý), 3) jeden z nich nastane vždy (tzn. nemůže nastat žádný jiný než jeden z jmenovaných), 4) každý výsledek má stejnou možnost, aby nastal. 9

Řešený příklad 2: V daném tvrzení rozpoznejte pojmy: náhodný pokus (NP), náhodný jev (NJ). Zapište množinu všech možných výsledků. a) Při hodu kostkou vyhraješ, když padne pětka. NP: hod kostkou M = {1, 2 , 3, 4, 5, 6} NJ: A = {5} 10

b) Při hodu kostkou vyhraješ, když padne liché číslo. NP: hod kostkou M = {1, 2 , 3, 4, 5, 6} NJ: B = {1; 3; 5} 11

c) Při zkoušce pevnosti určitého vlákna v tahu se vlákno nepřetrhlo. NP: zkouška pevnosti vlákna M = {přetrhne, nepřetrhne} NJ: C = {nepřetrhne} 12

d) Pokud padne na minci orel, získám pro své mužstvo míč. NP: hod mincí M = {orel, panna} NJ: D = {orel} 13

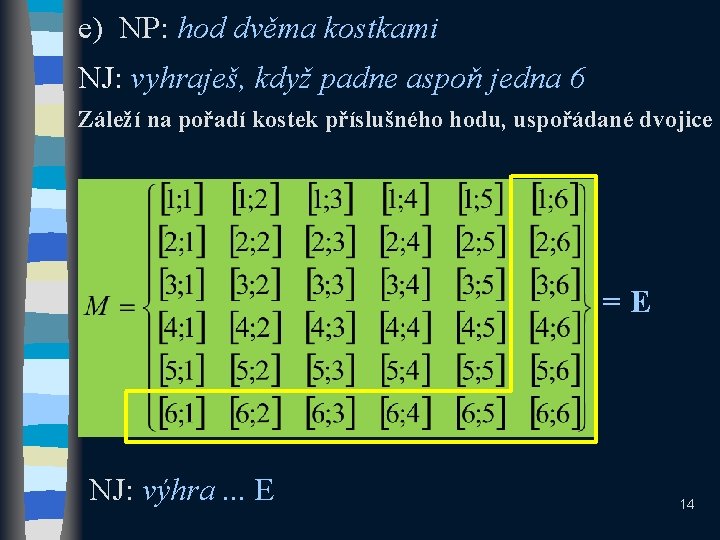
e) NP: hod dvěma kostkami NJ: vyhraješ, když padne aspoň jedna 6 Záleží na pořadí kostek příslušného hodu, uspořádané dvojice = E NJ: výhra. . . E 14

Závěr: n Ve 2. příkladu jsme názorně předvedli, že sledovaný jev je podmnožinou všech možných výsledků, které v dané situaci mohou nastat. n Pro jevy platí totéž co pro množiny a podmnožiny, jen se vžilo jiné názvosloví. 15

Jevy jako množiny n Důvod, proč je označujeme velkými písmeny. n Popisujeme je nějakou jistou vlastností, společnou všem prvkům daného jevu: 16

Jev jistý a nemožný n V daném pokusu rozeznáváme tolik jevů, kolik je podmnožiny všech možných výsledků (M) a mezi ně počítáme také: • celou množinu: A = M. . . jev jistý (každá množina je sama sobě podmnožinou) – například hodím kostkou 1 nebo 2 nebo 3 nebo 4 nebo 5 nebo 6 • prázdnou množinu: A = Ø. . . jev nemožný (množina prázdná je podmnožinou každé množiny) – například padnutí 7 na kostce, zjištění záporné délky životnosti výrobků, současné přetržení i nepřetržení vlákna, …. 17

Náhodné jevy a vztahy mezi nimi A B jev, který nastává právě tehdy, když nastane aspoň jeden z jevů A nebo B (sjednocení jevů A, B) 18

A B jev, který nastává právě tehdy, když nastanou oba jevy A, B současně (průnik jevů A, B) A B = Ø průnik jevů A, B je jev nemožný, tzn. jevy A, B se navzájem vylučují a říkáme, že A, B jsou jevy neslučitelné A´ jev opačný k jevu A, tzn. jev, který nastane právě tehdy, když jev A nenastane (negace jevu A) 19

Příklad 3: Znegujte dané věty A: Vyber lístky, které nebudou mít stejnou barvu. A´: Vyber lístky, které budou mít stejnou barvu. B: Vyber skupinu, ve které nebudou pouze dívky. B´: Vyber skupinu, ve které budou pouze dívky. C: . . . budou alespoň tři kuličky červené. C´: . . . budou nejvýše dvě kuličky červené. D: . . . budou maximálně čtyři dívky. D´: . . . bude minimálně pět dívek. E: . . . nebudou alespoň tři žáci připraveni. E´: . . . budou alespoň tři žáci připraveni. 20

JEDNODUCHÁ PRAVDĚPODOBNOST 21

Pravděpodobnost náhodného jevu V pokusu, jehož všechny možné výsledky jsou stejně pravděpodobné, je pravděpodobnost (ozn. P) sledovaného jevu (např. A) rovna podílu počtu příznivých výsledků danému jevu A (ozn. m) a počtu všech možných výsledků, které v daném pokusu mohou nastat (ozn. n). 22

Z definice plyne, že pravděpodobnost 1) jevu nemožného se rovná nule: 2) jevu jistého se rovná jedné: 3) jevu libovolného je v rozmezí hodnot od nuly do jedné: 23

Výsledek pravděpodobnosti se uvádí: 24

Kombinatorika – přehled vzorců 25

Na pořadí prvků ve skupině záleží nezáleží KOMBINACE VARIACE PERMUTACE 26

Řešený příklad 4: Ze třídy o 28 žácích urči losem 4 žáky, kteří se podrobí zkoušení. Urči počet n všech možných losování, neboli počet prvků množiny všech možných výsledků , jestliže určujeme čtveřici bez ohledu na pořadí zkoušených 27

Použijeme: KOMBINACE 28

Řešený příklad 5: Jaká je pravděpodobnost, že při hodu hrací kostkou padne šestka? n = 6, protože M = {1, 2 , 3, 4, 5, 6} m = 1, protože A = {6} 29

Řešený příklad 6: Jaká je pravděpodobnost, že při hodu hrací kostkou padne liché číslo? n = 6, protože M = {1, 2 , 3, 4, 5, 6} m = 3, protože A = {1, 3, 5} 30

Řešený příklad 7: Jaká je pravděpodobnost, jestliže je v osudí prvních 10 přirozených čísel že, vytáhnu prvočíslo n = 10, protože M = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} m = 4, protože A = {2, 3, 5, 7} 31

Řešený příklad 8: Jaká je pravděpodobnost, jestliže je v osudí prvních 10 přirozených čísel že, vytáhnu číslo dělitelné dvojkou nebo trojkou? n = 10, protože M = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} m = 7, protože A = {2, 3, 4, 6, 8, 9, 10} 32

Řešený příklad 9: Jaká je pravděpodobnost, jestliže je v osudí prvních 10 přirozených čísel že, vytáhnu číslo dělitelné dvojkou i trojkou? n = 10, protože M = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} m. A = 1, protože A = {6} 33

Řešený příklad 10: Ve třídě je 5 chlapců a 13 dívek. Jaká je pravděpodobnost, že ve čtyřčlenné skupině žáků této třídy budou a) tři chlapci a jedna dívka, b) právě dva chlapci? 34

výběr: 4 členná skupina n = C 4(18) = 3 060 a) jedna skupina: 3 CH, 1 D m = C 3(5). C 1(13) = 10. 13 = 130 35

výběr: 4 členná skupina n = C 4(18) = 3 060 b) právě (přesně) dva chlapci, tzn. musíme dobrat do skupiny ještě 2 dívky: 2 CH, 2 D m = C 2(5). C 2(13) = 10. 78 = 780 36

PŘÍKLADY NA PROCVIČENÍ Ø Jednoduchá pravděpodobnost 37

11. Ze třídy, ve které je 14 chlapců a 17 dívek, byla vybrána náhodně skupina pěti studentů. Jaká je pravděpodobnost, že v ní byli a) dva chlapci a tři dívky, b) tři chlapci a dvě dívky, c) čtyři chlapci a jedna dívka? [36, 42 %; 29, 13 %; 10, 02 %] 12. V urně je 8 bílých a 6 černých koulí. Náhodně vytáhneme 4 koule. Jaká je pravděpodobnost, že mezi nimi budou a) 2 bílé koule, b) 3 bílé koule, c) 4 bílé koule? [41, 96 %; 33, 56 %; 6, 99 %] 38

13. V sérii 40 výrobků je 5 zmetků. Náhodně vybereme tři výrobky. Jaká je pravděpodobnost, že mezi nimi budou a) dva zmetky, b) jeden zmetek, c) žádný zmetek? [3, 54 %; 30, 11 %; 66, 24 %] 14. Při hře 32 kartami (v sadě jsou 4 esa) bylo rozdáno 8 karet. Jaká je pravděpodobnost, že mezi nimi byla a)čtyři esa, b) dvě esa, c)jedno eso? [0, 19 %; 21, 49 %; 45, 03 %] 39

15. V osudí je 12 lístků bílých, 10 červených a 14 zelených. Náhodně vytáhneme 6 lístků. Jaká je pravděpodobnost, že mezi nimi budou a) 2 bílé, 2 červené a 2 zelené lístky, b) 1 bílý, 2 červené a 3 zelené lístky, c) 3 bílé, 1 červený a 2 zelené lístky? [13, 88 %; 10, 09 %; 10, 28 %] 40

SOUČET PRAVDĚPODOBNOSTÍ 41

n V následující kapitole budeme odvozovat pravděpodobnost sjednocení více jevů a na čem je výpočet závislý 42

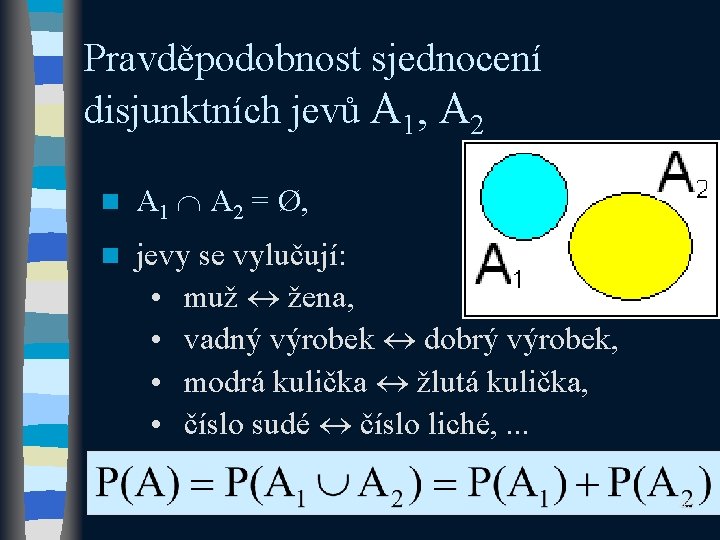
Pravděpodobnost sjednocení disjunktních jevů A 1, A 2 n A 1 A 2 = Ø, n jevy se vylučují: • muž žena, • vadný výrobek dobrý výrobek, • modrá kulička žlutá kulička, • číslo sudé číslo liché, . . . 43

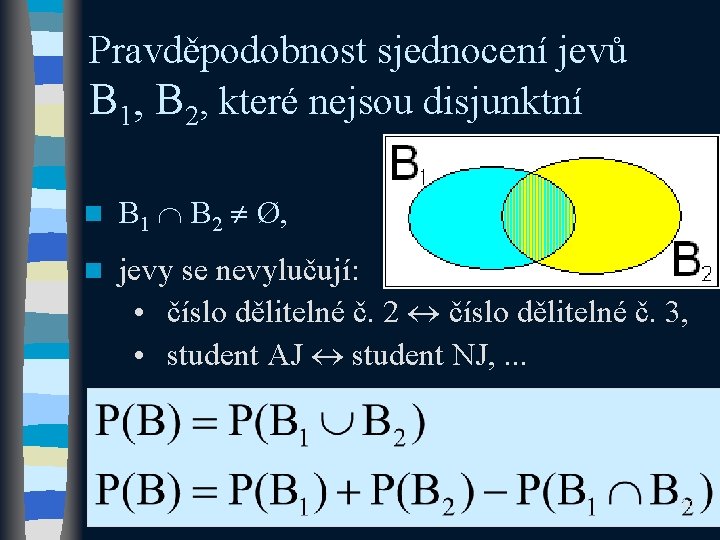
Pravděpodobnost sjednocení jevů B 1, B 2, které nejsou disjunktní n B 1 B 2 Ø, n jevy se nevylučují: • číslo dělitelné č. 2 číslo dělitelné č. 3, • student AJ student NJ, . . . 44

Řešený příklad 16: Ve třídě je 5 chlapců a 13 dívek. Jaká je pravděpodobnost, že ve čtyřčlenné skupině žáků této třídy a) bude nejvýše jeden chlapec, b) budou aspoň tři chlapci? 45

výběr: 4 členná skupina n = C 4(18) = 3 060 a) nejvýše 1 CH, tzn. buď 0 CH nebo 1 CH, 4 ve skupině 0 CH, 4 D nebo 1 CH, 3 D (jevy se vylučují) m. A = C 0(5). C 4(13) + C 1(5). C 3(13) = = 1. 715 + 5. 286 = 715 + 1 430 = 2 145 46

výběr: 4 členná skupina n = C 4(18) = 3 060 b) aspoň 3 CH, tzn. buď 3 CH nebo 4 CH, 4 ve skupině 3 CH, 1 D nebo 4 CH, 0 D (jevy se vylučují) m. B = C 3(5). C 1(13) + C 4(5). C 0(13) = = 10. 13 + 5. 1 = 130 + 5 = 135 47

PŘÍKLADY NA PROCVIČENÍ Ø Součet pravděpodobností 48

17. V sérii 28 výrobků jsou 3 zmetky. Jaká je pravděpodobnost, že mezi 4 náhodně vybranými výrobky bude nejvýše jeden zmetek? [95, 48 % ] 49

18. Při hře 32 kartami bylo rozdáno 6 karet. Jaká je pravděpodobnost, že mezi nimi budou alespoň dvě esa? [15, 04 %] 19. V osudí je 10 bílých, 5 černých a 6 zelených kuliček. Náhodně vytáhneme 4 kuličky. Jaká je pravděpodobnost, že mezi nimi budou nejméně 2 černé? [22, 8 %] 20. V urně je 5 černých, 7 bílých a 8 zelených koulí. Náhodně vybereme 3 koule. Jaká je pravděpodobnost, že a) budou mít tutéž barvu, b) každá koule bude mít jinou barvu? 50 [8, 86 %; 24, 56 % ]

PRAVDĚPODOBNOST OPAČNÉHO JEVU 51

Řešený příklad 21: V osudí je 6 kuliček modrých a 4 žluté. Jaká je pravděpodobnost, že vylosujeme 1 kuličku a) modrou, b) žlutou? 52

M = { n } Počet všech výsledků, které mohou nastat: n = 10 (vytáhnu jednu z deseti) n Počet výsledků příznivých jevu a) m. A = 6 (vytáhnu jednu ze šesti, z modrých) b) m. B = 4 (vytáhnu jednu ze čtyř, ze žlutých) n Výsledek: 53

Všimněte si n Součet pravděpodobností obou jevů A, B v příkladu 19 se rovná jedné: n Jevy A, B jsou tzv. doplňkové. 54

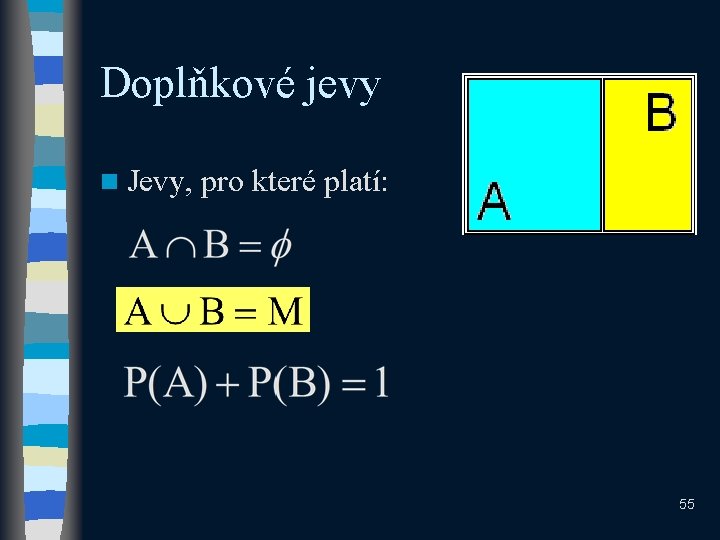
Doplňkové jevy n Jevy, pro které platí: 55

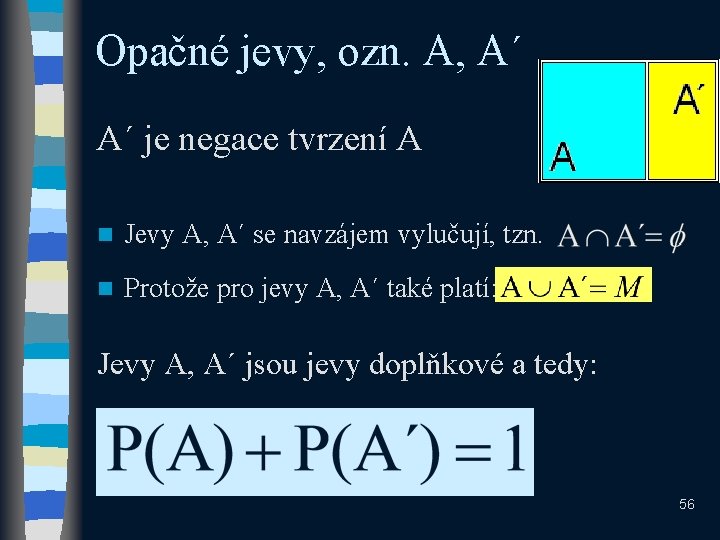
Opačné jevy, ozn. A, A´ A´ je negace tvrzení A n Jevy A, A´ se navzájem vylučují, tzn. n Protože pro jevy A, A´ také platí: Jevy A, A´ jsou jevy doplňkové a tedy: 56

Použití jevů opačných n Pravděpodobnost opačného jevu určujeme pouze tehdy, je-li to pro výpočet výhodnější. Tzn. počet možností příznivých opačnému jevu A´ je podstatně menší, než počet možností příznivých jevu výchozímu A. n Pravděpodobnost výchozího jevu A nakonec dopočteme jako doplněk pravděpodobnosti jevu opačného A´ do jedné: 57

Řešený příklad 22: Jaká je pravděpodobnost, že při hodu dvěma kostkami nepadne součet 2? 58

A … nepadne součet 2, tzn. padne součet: 3; 4; 5; 6; 7; 8; 9; 10; 11; 12 tzn. 10 různých možností a každou z nich početně určit určujeme jev opačný (negace výroku A) A´… padne součet 2, tzn. pouze jedna jediná možnost pro výpočet! n = V 2´(6) = 36 m. A´ = 1 {[1; 1]. . . jediná uspořádaná dvojice} 59

PŘÍKLADY NA PROCVIČENÍ Ø Pravděpodobnost opačného jevu 60

23. Ve třídě je 15 chlapců a 17 dívek. S jakou pravděpodobností mezi 4 vybranými zástupci nebudou samé dívky? [93, 38 % ] 61