Tenosusteooria ja matemaatiline statistika tenosus ja statistika Tundide











































































![Geomeetriline tõenäosus (II) Näited Lõigust [-1; 3] valitakse juhuslikult üks arv. – Kui suur Geomeetriline tõenäosus (II) Näited Lõigust [-1; 3] valitakse juhuslikult üks arv. – Kui suur](https://slidetodoc.com/presentation_image_h/c1b312f0699d66a181e5276bc011c2a0/image-80.jpg)
![Geomeetriline tõenäosus (III) Näide 1 Lõigust [-1; 3] valitakse juhuslikult üks arv. – Kui Geomeetriline tõenäosus (III) Näide 1 Lõigust [-1; 3] valitakse juhuslikult üks arv. – Kui](https://slidetodoc.com/presentation_image_h/c1b312f0699d66a181e5276bc011c2a0/image-81.jpg)














- Slides: 97

Tõenäosusteooria ja matemaatiline statistika (tõenäosus ja statistika)

Tundide jaotus • Kokku 35 tundi (üks 11. klassi matemaatika kursustest, nii kitsas kui ka laias matemaatikas) – Hindamine: • kontrolltööd (3 -4) • praktiline töö (statistikast)

Materjalid • VIKO: http: //viko. edu. ee

• Õpikud: – K. Velsker, L. Lepmann, T. Lepmann “Matemaatika XI klassile” – T. Tõnso, A. Veelmaa “ Matemaatika 12. klassile” – O. Prinits “Matemaatilise statistika ja tõenäosusteooria elemente keskkoolile : fakultatiivkursus” (1977) – arvukalt Internetist leitavad allikad

võõrkeelsed: – В. С. Лютикас “Факультативный курс по математике / теория вероятностей“ (1990) – C. M. Grinstead, J. Laurie Snell “Introduction to probability. ” (vt http: //www. dartmouth. edu/~chance/teaching_aids/books_arti cles/probability_book/book. html)

Ajaloost • Tekkinud 17. sajandil seoses hasartmängudega (kaardid, täringud) • Antoine Gombaud’ (Chevalier de Méré) probleemid – kirjavahetus de Fermat’ ja Pascal’iga

De Méré probleem • Teatud võrdsete võimalustega mängu mängitakse kindla arvu võitudeni (näiteks 3 võiduni). Kui mingil põhjusel mäng katkestatakse, kuidas tuleks siis panused jaotada (kui jaotada ausalt!)? Kui näit. esimene mängija on katkestamise momendiks võitnud kaks ja teine mängija ühe mängu? Kas jagada suhtes 2: 1? Või mingis muus suhtes?

Ajaloost • Huygens – esimene tõenäosusteooria raamat 1657. a • Bernoulli – Bernoulli valem, Bernoulli suurte arvude seadus • Gauss – Gaussi kõver • Tšebõšev (ingl k Chebychev) – suurte arvude seadus (katseliselt määratava suuruse tõelise väärtuse parimaks lähendiks on katsetulemuste aritmeetiline keskmine, mis on seda usaldusväärsem, mida pikema katseseeria põhjal see on leitud) • Kolmogorov – tõenäosusteooria aksiomaatika looja ("Grundbegriffe der Wahrscheinlichkeitsrechnung” (“Tõenäosusteooria põhimõisted”), 1933

Põhimõisted • Katse – toiming, mille korraldamise protseduur on fikseeritud; katse käigus jälgitakse, kas teatud sündmused toimuvad või mitte • Sündmus – katse tulemus Näide 1 • Katseks on täringu viskamine • Sündmused: – saadakse 1, 2, 3, 4, 5 või 6 silma – saadakse paarisarv silmi – silmade arv jagub 3 -ga jne

• Näide 2 • Visatakse korraga kahte täringut • Sündmused: – Summana saadakse 2, 3, 4, …, 12 silma – Ühel täringul on suurem silmade arv kui teisel – Summana saadakse vähemalt 3 silma – Mõlemal täringul on sama silmade arv

Sündmuste liigitamine • Näide 3 • Katseks on ühe täringu viskamine • A – saadakse 7 silma võimatu sündmus B – saadakse 1, 2, 3, 4, 5 või 6 silma C – saadakse 4 silma juhuslik sündmus kindel sündmus

• Võimatu sündmus – sündmus, mis antud katse käigus ei saa esile tulla; tähistus • Kindel sündmus – sündmus, mis antud katses kindlasti toimub; tähistus • Juhuslik sündmus – sündmus, mis antud katse käigus võib toimuda, võib aga ka mitte toimuda; tähistatakse A, B, C, … vahel kasutatakse ka indekseid: A 1, A 2, A 3, …

Põhimõisted (II) • Vastandsündmus – seisneb sündmuse A mittetoimumises; tähistus (loe: A kaetud) • Näide Katseks on kahe täringu viskamine A – summana saadakse vähemalt 6 silma ( - summaks on 2, 3, 4 või 5 silma (<6) )

Ülesanne 1 Sündmus A Mündi viskamisel saadakse “kiri” Kaardipakist tõmmatakse välja kolm kaarti, mis kõik on ärtu mastist Kolmest vastutulijast vähemalt üks on naine Sündmuse kirjelduses esineb sõnapaar “vähemalt üks” … x<4 Vastandsündmus

Ülesanne 1 Sündmus A Vastandsündmus Mündi viskamisel saadakse “kiri” Mündi viskamisel saadakse “kull”. Kaardipakist tõmmatakse välja kolm kaarti, mis kõik on ärtu mastist Kolme kaardi hulgas on vähemalt üks “mitteärtu”. Kolmest vastutulijast vähemalt üks on naine Kolme vastutulija hulgas naisi pole. Sündmuse kirjelduses esineb sõnapaar “vähemalt üks” … Vastandsündmuse kirjelduses tuleb kasutada: “mitte ükski” (“mitte ühtegi”) x<4

Põhimõisted (III) • Sõltumatud sündmused – kui katse kordamisel ühe sündmuse toimumine ei mõjuta teise sündmuse toimumist • Sõltuvad sündmused – ühe sündmuse toimumisest sõltub teise sündmuse toimumine

• Näide sõltumatute sündmuste kohta Täringut visatakse järjest kaks korda. A – esimesel viskel saadakse 4 silma B – teisel viskel saadakse 3 silma Sündmused A ja B on sõltumatud, sest teise viske tulemus ei sõltu esimese katse tulemusest.

• Näide sõltuvate sündmuste kohta Kaardipakist võetakse järjest kaks kaarti. Esimest kaarti ei panda enne teise võtmist pakki tagasi. A – esimene kaart on ärtu B – teine kaart on samuti ärtu Kui A toimub, siis on B toimumiseks 12 võimalust. Kui A ei toimu, siis on B toimumiseks 13 võimalust. Sündmuse B toimumine on sõltuv sündmuse A toimumisest. A ja B on sõltuvad sündmused.

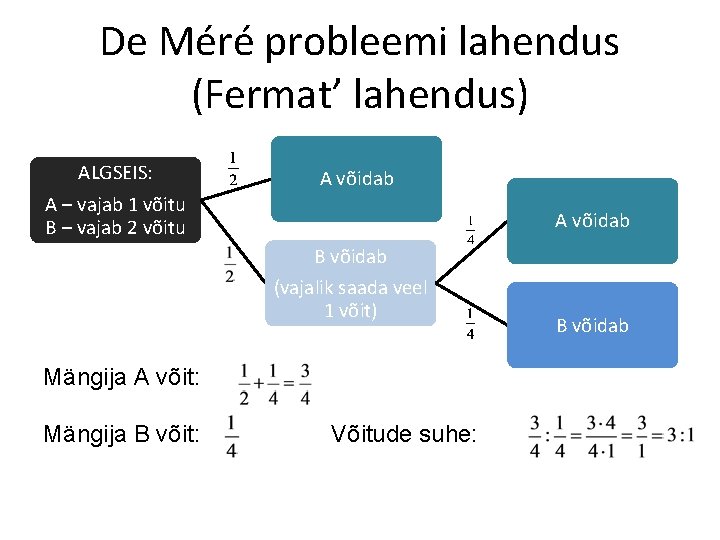
De Méré probleemi lahendus (Fermat’ lahendus) ALGSEIS: A – vajab 1 võitu B – vajab 2 võitu A võidab B võidab (vajalik saada veel 1 võit) Mängija A võit: Mängija B võit: Võitude suhe: B võidab

Nuputamiseks Teatud võrdsete võimalustega mängu mängitakse nelja võiduni. Enne mängu panustab kumbki mängija 100 raha. Katkestamise momendiks on mängija A võitnud kolm mängu, mängija B aga ühe mängu. Kuidas tuleks panustatud raha (200) jaotada?

/jätk/ Panuste jagamine. Kokku on 200 raha. Jagada tuleb suhtes 7: 1. Osade koguarv on 8. Üks osa on Mängija A peab saama: mängija B peab saama:

Põhimõised (III) • Teineteist välistavad sündmused – sündmused, millest ühe toimumisel on teise sündmuse toimumine samal katsel võimatu • Näide Visatakse täringut. A – saadakse 4 silma, B – saadakse 5 silma. Sündmused A ja B on teineteist välistavad sündmused. • Aga: Visatakse korraga kahte täringut. C – saadud summa jagub 3 -ga D – saadud summa jagub 2 -ga Sündmused C ja D ei ole teineteist välistavad (näit. kui summa on 12, siis see jagub nii 2 -ga kui ka 3 -ga).

Ülesanne 2 • Iga sündmuse kohta märkida, kas ta on juhuslik, võimatu või kindel sündmus. – Täringuviskel saadakse viis silma. – Rakveres paistab täna õhtul (7. novembril) kell 23. 45 päike. – Raamatus on 200 lehekülge. Seda raamatut juhuslikust kohast avades avame ta 45. ja 46. lehekülje vahelt. – Kahe täringu koos viskamisel saadakse summaks 5 silma.

Ülesanne 2(jätk) – Kolme täringu koos viskamisel saadakse summaks 20 silma. – Normaaltingimustes hakkab vesi keema 100 kraadi juures. – Vesi hakkab keema 100 kraadi juures. – Täna kutsutakse geograafiatunnis vastama Peeter (Peeter on antud klassi õpilane ning täna ka koolis, geograafiatunnis on ta kohal).

Ülesanne 2 (jätk) – 100 aasta pärast on 100 m jooksu maailmarekord 9, 2 sekundit. – Korvis on 2 musta ja 4 valget kuulikest. Võetakse üks kuul ning saadakse sinine kuul. – Sajast säästulambist on kaks aastat pärast kasutuselevõtmist töökorras vähemalt 90 lampi.

Ülesanne 3 • Iga sündmuse kohta märkida, mis on tema vastandsündmuseks. A – täringuviskel saadakse paarisarv silmi B – nelja vastutulija hulgas on vähemalt üks blondiin D – kaardipakist tõmmatud 3 kaarti on kõik ässad E – saja detaili hulgas on vähemalt 80 kvaliteetset detaili F – kolme täringu viskamisel saadakse summaks vähemalt 4

Ülesanne 4 • Kas sündmused on sõltumatud või sõltuvad? – Täringut visatakse kaks korda. A – esimesel viskel saadakse paarisarv silmi B – teisel viskel saadakse 4 silma – Korvis on 4 õuna ja 5 pirni. Võetakse kolm puuvilja. A – esimesena saadakse õun. B – teisena saadakse õun. C – kolmandana saadakse õun.

Ülesanne 4 (jätk) • Korvis on 4 valget ja 5 punast kuulikest. Võetakse üks kuul. Pärast tema värvi kindlakstegemist pannakse kuulike korvi tagasi. Samuti toimitakse veel kaks korda. A – esimesena saadakse valge kuul B – teisena saadakse valge kuul C – kolmandana saadakse kolmas kuul Kas A, B, C on sõltumatud või sõltuvad?

Ülesanne 5 • Kas sündmused A ja B on teineteist välistavad sündmused või mitte? – Visatakse korraga kahte täringut. A – summana saadakse 7 silma B – ühe täringuga saadakse 5 silma, teise täringuga 2 silma – Visatakse korraga kahte täringut A – mõlema täringuga saadakse paarisarv silmi B – summana saadakse 11 silma

Ülesanne 5 (jätk) – Kaardipakis on 52 kaarti. Tõmmatakse 4 suvalist kaarti. A – saadud kaartide hulgas on 3 ässa B – saadud kaartide hulgas on 3 ärtu mastist kaarti – Kaardipakis on 36 kaarti. Tõmmatakse üks kaart. A – saadud kaart on ärtu kuningas B – saadud kaart on pildikaart

Bernoulli valem Gaussi kõver (normaaljaotus)

Gaussi kõver

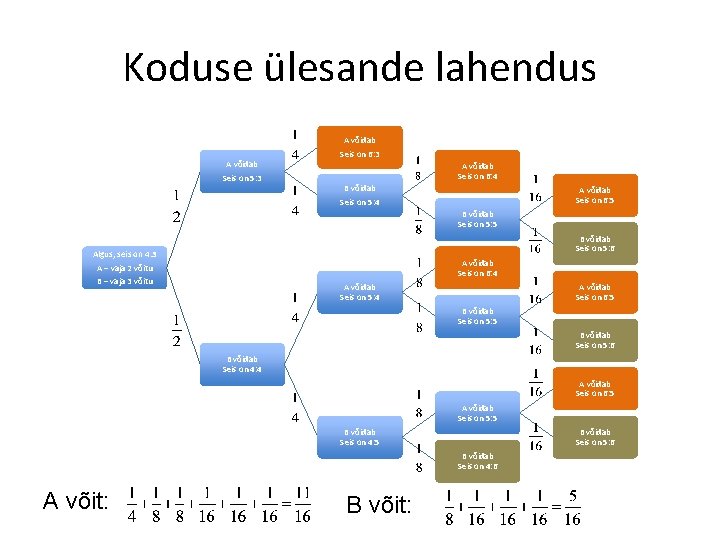
Koduse ülesande lahendus A võidab Seis on 5: 3 Seis on 6: 3 A võidab Seis on 6: 4 B võidab A võidab Seis on 6: 5 Seis on 5: 4 B võidab Seis on 5: 5 B võidab Seis on 5: 6 Algus; seis on 4: 3 A – vaja 2 võitu A võidab Seis on 6: 4 B – vaja 3 võitu A võidab Seis on 5: 4 A võidab Seis on 6: 5 B võidab Seis on 5: 6 B võidab Seis on 4: 4 A võidab Seis on 6: 5 A võidab Seis on 5: 5 B võidab Seis on 4: 5 B võidab Seis on 5: 6 B võidab Seis on 4: 6 A võit: B võit:

/jätk/ Panuste jagunemine: Vastus. Panused tuleb jaotada suhtes 11: 5.

Tõenäosuse mõiste Tõenäosus – sündmuse toimumise võimalikkuse määr (arv, mis iseloomustab sündmuse toimumise võimalikkust). Eristatakse järgmisi tõenäosuse arvutamise võtteid: • klassikaline tõenäosus, • geomeetriline tõenäosus, • statistiline tõenäosus.

Klassikaline tõenäosus p – tõenäosus A – sündmus m – soodsate võimaluste arv sündmuse A toimumiseks n – kõikide võimaluste arv Võimatu sündmuse korral Kindla sündmuse korral Juhusliku sündmuse korral Sündmuse ja vastandsündmus:

Näide 1 1. Visatakse täringut. A – saadakse 6 silma, B – saadakse 5 silma n= m= p(A) = p(B) =

Näide 1 (lahendus) 1. Visatakse täringut. A – saadakse 3 silma n=6 m=1 (6 erinevat võimalikku tulemust) (saadakse 3 silma)

Näide 2 2. Visatakse korraga kahte täringut. A – summana saadakse 8 silma n = ……………. . m = ……………. p(A) = …………. .

Näide 2 (idee) 2. Visatakse korraga kahte täringut. A – summana saadakse 8 silma Tulemused võiks esitada tabelis: I täringul saadud silmade arv II täringul saadud silmade arv 1 1 2 3 4 5 6

Näide 2 (lahendus) 2. Visatakse korraga kahte täringut. A – summana saadakse 8 silma Tulemused võiks esitada tabelis: II täringul saadud silmade arv 1 2 3 4 5 6 7 8 9 4 5 6 7 8 9 10 11 12 n = 36 m = 5

Näide 3 Visatakse korraga kolme täringut. Kui suur on tõenäosus, et summana saadakse vähemalt 4 silma? n=… m=… p(A) = …

Näide 3 (idee) Visatakse korraga kolme täringut. Kui suur on tõenäosus, et summana saadakse vähemalt 4 silma? Lahendusidee: kui võimaluste arv on suur, siis tasuks kaaluda üleminekut vastandsündmusele. Praegu on vastandsündmuseks: summana saadakse ……………. .

Näide 3 (lahendus) Praegu on vastandsündmuseks: summana saadakse ……………. . Soodsaid võimalusi vastandsündmuse toimumiseks m = …… Seega Otsitud tõenäosuse leiame seosest Avaldame p(A):

Ülesanded tõenäosuse klassikalise valemi rakendamisele(I) 1. Täringut visatakse 5 korda järjest. Kui suur on tõenäosus, et neljandal katsel saadakse 5 silma? 2. Täringut visatakse 100 korda. Neist 20 korral saadakse 5 silma. Kui suur on tõenäosus, et 101. korral saadakse samuti 5 silma?

Ülesanded tõenäosuse klassikalise valemi rakendamisele(II) 3. Kaardipakist tõmmatakse juhuslikult üks kaart. Kui suur on tõenäosus, et saadakse pilt (piltideks on sõdur, emand, kuningas, äss)? 4. Kaardipakist tõmmatakse juhuslikult kaks kaarti. Kui suur on tõenäosus, et nad mõlemad on ärtu mastist?

Ülesanded tõenäosuse klassikalise valemi rakendamisele(III) 5. Klassis on 15 poissi ja 10 tüdrukut. Ajalootunnis kutsutakse vastama üks õpilastest. Kui õpilase väljavalimine on juhuslik, kui suur on siis tõenäosus, et vastama kutsutakse poiss? 6. Korvis on 2 valget, 5 musta ja 6 sinist palli. Võetakse 10 palli (neid tagasi panemata). Kui suur on tõenäosus, et korvi jäävad vaid valged pallid?

Ülesanded tõenäosuse klassikalise valemi rakendamisele(IV) 7. Mustkunstniku 52 -lehelises kaardipakis on vaid ärtu ässad ning risti kuningad (mõlemaid võrdselt). Võetakse 27 kaarti (neid tagasi panemata). Kui suur on tõenäosus, et nende kaartide hulgas on vähemalt üks äss? 8. Peeter ja Ants sõlmivad järgmise kihlveo. Neutraalne isik viskab kolme täringut korraga. Peeter võidab, kui kolme täringu summana saadakse vähemalt 10 silma, Ants võidab vastupidisel juhul. Kumma poisi võidu tõenäosus on suurem?

Ülesanded tõenäosuse klassikalise valemi rakendamisele(V) 9. Missugune on tõenäosus, et 1995. a sündinud inimene on sündinud a) veebruaris b) mingi kuu viimasel päeval 10. Kaardipakist on võetud mõned kaardid. Kui suur on tõenäosus, et järgmisena võetav kaart on a) ruutu mastist b) kuningas c) 10 või emand

Ülesanded tõenäosuse klassikalise valemi rakendamisele(VI) 11. Urnis on 8 valget, 7 punast ja 5 sinist kuuli. Võetakse juhuslikult üks kuul. Kui suur on tõenäosus, et see kuul on a) valge, b) punane, c) sinine 12. Urnist võetakse 3 kuuli, neid tagasi panemata. Kui suur on tõenäosus, et need kuulid on kõik valged?

Ülesanded tõenäosuse klassikalise valemi rakendamisele(VII) 13. Klassis on 12 noormeest ja 18 tütarlast. Nimekirjast valitakse juhuslikult 3 õpilast. Kui suur on tõenäosus, et valitakse tüdrukud? 14. Urnis on valged ja punased kuulid. Valitakse üks juhuslik kuul. Punase kuuli valimise tõenäosus on 0, 3. Kui suur on valge kuuli valimise tõenäosus?

15. Münti visatakse üks kord. Missugune on “kirja” saamise tõenäosus? a) b) c) d) Millised järgmistest väidetest on tõesed Mündi järjestikusel viskamisel tuleb igal teisel viskel “kiri”; väär kui münti visatakse kaks korda, siis emmalkummal viskel tuleb “kiri”; väär kui münti visatakse 100 korda, siis 50 korral tuleb “kiri”; väär kui münti visatakse sadu kordi, siis umbes tõene 50% visetest saadakse “kiri”

Probleemülesanne Karbis on kuulikesed: Võetakse kaks kuuli. Kui suur on tõenäosus, et saadakse sama värvi kuulikesed?

I lahendus Kui kuulikesed võeti korraga, siis on võimalused kahe kuuli saamiseks järgmised: Sobivaiks on esimene ja kolmas, seega vastav tõenäosus on

II lahendus Kui kuulikesi ei võetud korraga, siis on võimalused kahe kuuli saamiseks järgmised: Sobivaiks on esimene ja neljas, seega vastav tõenäosus on

III lahendus Nummerdame kuulikesed: Kui võtta kuulid korraga, siis on kahe kuuli saamiseks järgmised võimalused: Sama värvi on kuulid esimesel ja kuuendal juhul, seega

Kolm varianti Milline on õige? ? ? Kuidas saaks kontrollida? Kas on veel võimalusi? ?

IV lahendus Nummerdame kuulikesed: Kui kuulid ei ole võetud korraga, siis on kahe kuuli saamiseks järgmised võimalused: Tõenäosus:

Järeldus Võimaluste arvu kindlakstegemisel peame arvestame kõikide elementaarsündmustega. Elementaarsündmused (lihtsündmused) – • antud katse kõik võimalikud tulemused • üksteist välistavad • võrdvõimalikud

8. ülesanne Peeter ja Ants sõlmivad järgmise kihlveo. Neutraalne isik viskab kolme täringut korraga. Peeter võidab, kui kolme täringu summana saadakse vähemalt 10 silma, Ants võidab vastupidisel juhul. Kumma poisi võidu tõenäosus on suurem? Leida need tõenäosused.

Antsu võit • 3 silma: • 4 silma: • 5 silma: • 6 silma: 111 112 113 122 114 123 222 121 131 212 … … 211 311 221

• 7 silma: • 8 silma: 115 124 133 223 116 125 134 224 233 … … … … …

• 9 silma: 126 … 135 … 144 … 225 … 234 … 333 KOKKU: 81 soodsat võimalust;

Kombinatoorika on matemaatika haru, mis uurib etteantud hulga elementide kombineerimise võimalusi. Koolimatemaatikas uuritakse järgmisi võimalusi: • permutatsioonid • variatsioonid • kombinatsioonid

Permutatsioonideks nimetatakse antud hulga elementidest moodustatud kõikvõimalikud järjestusi. Permutatsioonide arvu tähistatakse sümboliga Pn P 1 = 1 P 2 = 2 P 3 = …

P 1 = 1 P 2 = 1 2 P 3 = 6 = 1 2 3 P 4 = 24 =1 2 3 4 P 5 =. . . P 6 = … Üldkujul: Pn = 1 2 … n ehk Pn = n! faktoriaal

Erand Permutatsioonide arv 0 elemendist tuleb defineerida: P 0 = 1

Näited • Moodustada kõik võimalikud kolmesõnalised laused sõnadest KEEGI, SIIN, ON. • Mitu erinevat lauset saab moodustada sõnadest TIHTI, TAEVAS, NÄHTI, TÄHTI. Kirjutada need laused ning püüda nad võimalikult kiiresti (ja veatult!) ette lugeda.

Faktoriaal kalkulaatoriga • n! või x! • teha kindlaks suurim tavalise kalkulaatoriga leitav faktoriaal

Ülesanded 1. Pere viis last reastatakse juhuslikus järjekorras. Kui suur on tõenäosus, et lapsed paigutuvad ritta vanuse järgi (kas nooremast vanemani või vastupidi)? 2. Mitmel erineval viisil saab bussi siseneda kümme reisijat? Kui kaua aega kulub kõikvõimalike variantide “läbimängimiseks”, kui 10 inimese sisenemine võtab aega 1 minuti ja päevas jõuab katsetada 8 tundi?

3. Isa on kirjutanud aadressid viiele ümbrikule ja pannud need lauale. Teises hunnikus on samas järjekorras viis kutset erinevatele sõpradele. 5 -aastane poeg tahtis isa aidata, kui isa oli toast lahkunud. Ta võttis kutsed, kuid need kukkusid maha. Korjanud kõik jälle kokku, hakkas ta kutseid ükshaaval ümbrikutesse panema. Mitu erinevat varianti kutsete panekuks saaks nii tekkida?

4. Igal inimesel on neli vanavanemat (kaks vanaisa ja kaks vanaema). Mitu vanavanemate vanavanemat on igal inimesel? Kui palju on vanavanematel vanavanemate vanavanemaid?

5. Lihtsustada avaldis: 1) 2) 3)

05. 12. 2012 11 T • Kodune ülesanne Nr 732: 5! = 120 Nr 736: 3! = 6 võimalust AOS OAS SAO ASO OSA SOA Nr 737: 7! või 12! 7! = 5040 12! = 479 001 600


Ülesanded õpikust • • Nr 739 Nr 740 Nr 741 Nr 742 NB! Nr 743 Nr 744 Nr 745 anagrammid KALEV VELAK

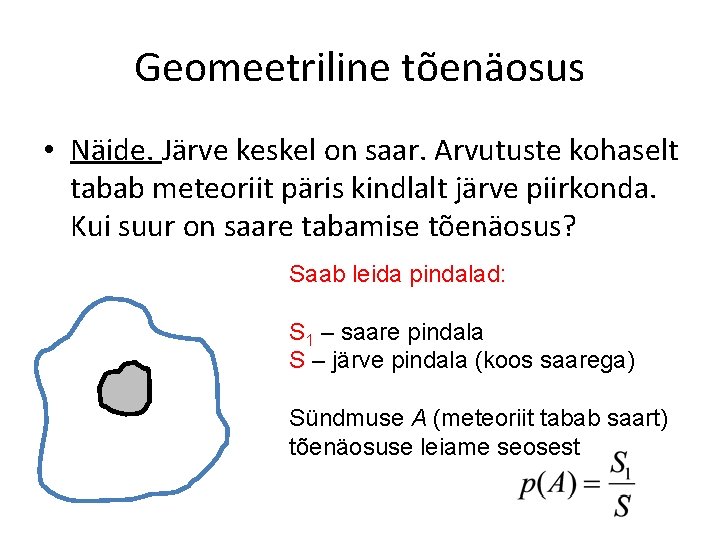
Geomeetriline tõenäosus Näide. Järve keskel on saar. Arvutuste kohaselt tabab meteoriit päris kindlalt järve piirkonda. Kui suur on saare tabamise tõenäosus?

Geomeetriline tõenäosus • Näide. Järve keskel on saar. Arvutuste kohaselt tabab meteoriit päris kindlalt järve piirkonda. Kui suur on saare tabamise tõenäosus? Saab leida pindalad: S 1 – saare pindala S – järve pindala (koos saarega) Sündmuse A (meteoriit tabab saart) tõenäosuse leiame seosest

Geom. tõenäosuse korral eeldatakse, et piirkonna iga punkti tabamiseks on võrdsed võimalused. Suhtarvu leidmisel võib jagada erinevaid mõõtmeid (pikkus, pindala, ruumala).
![Geomeetriline tõenäosus II Näited Lõigust 1 3 valitakse juhuslikult üks arv Kui suur Geomeetriline tõenäosus (II) Näited Lõigust [-1; 3] valitakse juhuslikult üks arv. – Kui suur](https://slidetodoc.com/presentation_image_h/c1b312f0699d66a181e5276bc011c2a0/image-80.jpg)
Geomeetriline tõenäosus (II) Näited Lõigust [-1; 3] valitakse juhuslikult üks arv. – Kui suur on tõenäosus, et valitud arv on 2, 5? 2, 5 -1 3 – Kui suur on tõenäosus, et valitud arv on vähemalt 0, 5 (≥ 0, 5)? -1 0, 5 x≥ 0, 5 3
![Geomeetriline tõenäosus III Näide 1 Lõigust 1 3 valitakse juhuslikult üks arv Kui Geomeetriline tõenäosus (III) Näide 1 Lõigust [-1; 3] valitakse juhuslikult üks arv. – Kui](https://slidetodoc.com/presentation_image_h/c1b312f0699d66a181e5276bc011c2a0/image-81.jpg)
Geomeetriline tõenäosus (III) Näide 1 Lõigust [-1; 3] valitakse juhuslikult üks arv. – Kui suur on tõenäosus, et valitud arv on 2, 5? Lahendus Geomeetrilise tõenäosuse valemi järgi – Kui suur on tõenäosus, et valitud arv on vähemalt 0, 5 ? Lahendus Geom. tõenäosuse valemi järgi

Järeldus Sündmus võib toimuda ka siis, kui tõenäosus on null. /Teame, et võimatu sündmuse tõenäosus on 0; seega vastupidine väide ei kehti. / Kasutatakse ka terminit praktiliselt võimatu sündmus.

Geomeetriline tõenäosus (IV) • Näide 2 Ring, mille üks sektor on värvitud punast värvi, hakkab kiiresti pöörlema ümber keskpunkti. Kui suur on tõenäosus, et selle ringi torkamisel nõelaga tabatakse punast osa? Sektori nurk on 300.

Geomeetriline tõenäosus (IV) • Näide 2 Ring, mille üks sektor on värvitud punast värvi, hakkab kiiresti pöörlema ümber keskpunkti. Kui suur on tõenäosus, et selle ringi torkamisel nõelaga tabatakse punast osa? Sektori nurk on 300. Geomeetrilise tõenäosuse valemi põhjal:

Ülesanne 1 Kui suur on värvitud piirkonna tabamise tõenäosus? r 2 r

Ülesanne 2 Bussid väljuvad lõpp-peatusest iga poole tunni tagant ja avavad sisenemiseks uksed viis minutit enne väljumist. a) Kui suur on tõenäosus, et reisija saab peatusesse saabudes kohe bussi siseneda? b) Kui suur on tõenäosus, et ta peab ootama bussi pääsemist üle 10 minuti?

Ülesanne 3 Jalakäijate fooris lülitub roheline tuli sisse iga kolme minuti tagant. Roheline tuli põleb 1 minuti ja 20 sekundit. Kui suur on tõenäosus, et ülekäigukohale jõudnud jalakäija a) saab kohe teed ületada; b) peab ootama rohelist tuld?

Statistiline tõenäosus Tugineb Bernoulli suurte arvude seadusele. Toimitakse nõnda: • sooritatakse k sõltumatut katset • tehakse kindlaks sündmuse A toimumiste arv • arvutatakse nn suhteline sagedus • statistiline tõenäosus:

Statistiline tõenäosus (II) Näide 1 Korvpallur on sooritanud iga treeningu lõpus seeria vabaviskeid: Visete arv 80 100 120 100 100 Tabamuste arv 70 85 100 80 85 90 90 95 85 90 A – korvpallur tabab vabaviske

Statistiline tõenäosus (II) Näide 2 Kui suur on tõenäosus, et sünnib poiss? Tervise Arengu Instituudi (TAI) andmetel 1992 -2011 Poisse 147172 Tüdrukuid 138500 KOKKU 254741 Poisi sündimise tõenäosus:

Tuntud näiteid ajaloost • Georges de Buffon (1707 -1788) viskas münti 4040 korda, vapp 2048 korral; suhteline sagedus 0, 507 • Karl Pearson (1857 -1936) viskas münti 12000 korda, vapp 6019; suhteline sagedus 0, 5016; II seeria 24000 korda, vapp 12012 korral; suhteline sagedus 0, 5005 Klassikalise valemi järgi: p(A) = 0, 5

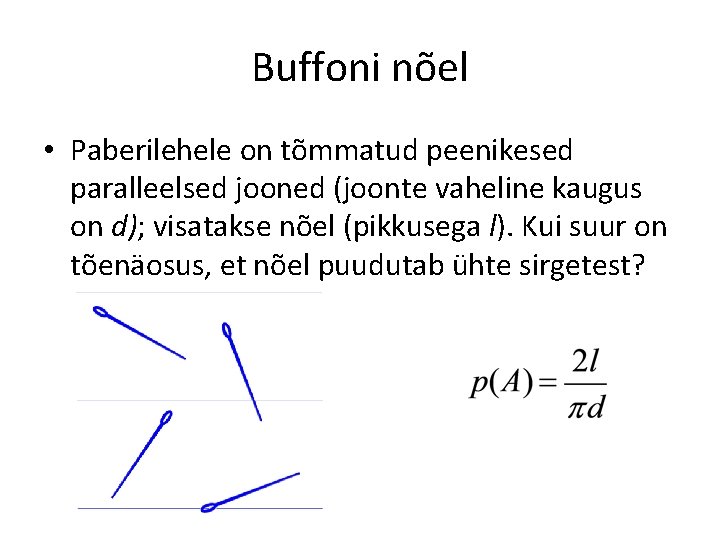
Buffoni nõel • Paberilehele on tõmmatud peenikesed paralleelsed jooned (joonte vaheline kaugus on d); visatakse nõel (pikkusega l). Kui suur on tõenäosus, et nõel puudutab ühte sirgetest?

Ülesanded (I) 1. Korvpallur on viimase hooaja ametlikes mängudes sooritanud kokku 2435 lähipositsiooni pealeviset, neist tabanud aga 1629. Kui suur on tõenäosus, et täna toimuvas mängus see korvpallur tabab oma viienda pealeviske? 2. Visatakse ühte täringut. Kui üheksal korral järjest on saadud 6 silma, kui suur on siis tõenäosus, et kümnendal korral saadakse ka 6 silma?

Ülesanded (II) 3. Ukse mõõtmed on 1 x 2 meetrit. Ukses on aknake mõõtmetega 2 x 5 detsimeetrit. Ust pommitatakse/visatakse lumepallidega. Kui suur on tõenäosus, et tabatakse aknaruutu? 4. Arvutisimulatsioonis imiteeritakse teatud katset. Seni läbiviidud 109 katses on sündmus A toimunud ligikaudu 4, 4 108 korda. Kui suur on sündmuse A toimumise tõenäosus?

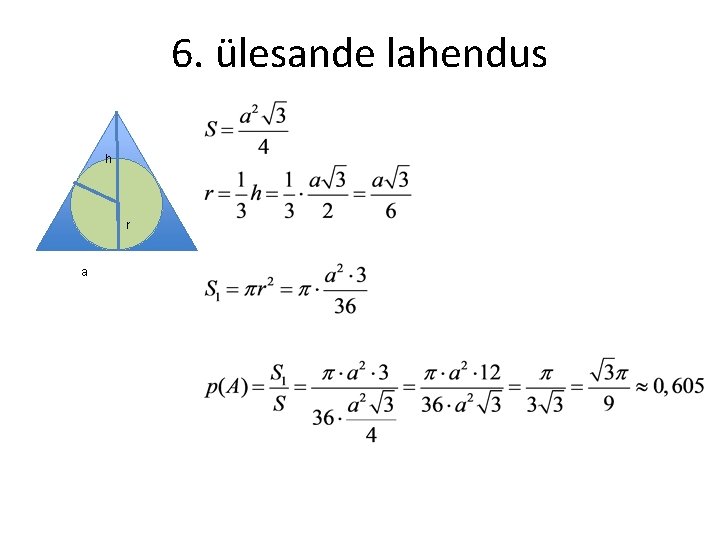
Ülesanded (III) 5. Tabelis on kirjeldatud sündmuse A esiletulek paljudes katseseeriates. Kui suur on tõenäosus, et homme läbiviidavas katses sündmus A siiski ei toimu? Katsete 100 arv 100 100 100 n 90 95 80 95 95 90 95 5. Kui suur on tõenäosus, et võrdkülgses kolmnurgas juhuslikult valitud punkt on ühtlasi kolmnurga siseringi punkt?

6. ülesande lahendus h r a

Ülesanded (IV) 7. Urnis on 3 valget ja 5 musta kuulikest. Võetakse järjest 3 kuulikest (neid tagasi panemata). Kui on teada, et valgeid kuulikesi ei saadud, kui suur on siis tõenäosus, et järgmise kuuli võtmisel saadakse siiski valge kuul? 8. Laual on kaardid numbritega 1, 2, 3, 4, 5. Väike Mall laob neist rea. Kui palju on erinevaid võimalusi? Kui suur on tõenäosus, et ta laob 5 -ga jaguva arvu?