Tendance centrale Ex Examen de philo La moyenne

Tendance centrale § Ex: Examen de philo. § La moyenne était de 34%. § Permet de caractériser une série statistique au moyen d’une valeur ou modalité typique

Le mode § La valeur ou la modalité la plus fréquente. § Ex: Examen de Méthodes quantitatives § Notes: 9, 8, 9, 10, 7, 7, 2, 8, 5, 5, 7, 9, 7, 7, 6, 6, 3, 7, 7, 9, 10, 3, 6, 7, 6, 3, 7, 8, 4 § Mo=? (Utilisez Excel pour vous aider) § Ouvrir fichier Excel « Exemple 1 mode » § Faire un tableau de fréquences d’abord § Si lettres ? : A, B, C, C, D, C, B, B, A, D, C, C, C, B, A, C, C, B, D, C, B, C, C § Mo=?

La médiane § Divise une série statistique ordonnée en 2 groupes comptant environ 50% des données § C’est le centre de position § On essaie d’avoir le même nb d’individus à gauche et à droite du centre de position § Notes: 9, 8, 9, 10, 7, 7, 2, 8, 5, 5, 7, 9, 7, 7, 6, 6, 3, 7, 7, 9, 10, 3, 6, 7, 6, 3, 7, 8, 4 § Md=? § Ouvrir fichier Excel « Exemple 1 mode » § Langue parlée: A, F, F, E, R, R, A, A, E, i, A, E, E, A, i, F § Md=?

La moyenne § Somme des données/nb de données § Exemple facile: Combien de bières buvezvous par semaine: 1, 1, 2, 3, 3, 3, 4, 4 § Créer un tableau de fréquences et refaire le calcul § Valeur x fréq +etc/nb données § Notes: 9, 8, 9, 10, 7, 7, 2, 8, 5, 5, 7, 9, 7, 7, 6, 6, 3, 7, 7, 9, 10, 3, 6, 7, 6, 3, 7, 8, 4 § Trouvez la moyenne de la classe à partir du tableau des fréquences

Pourquoi ne pas toujours prendre la moyenne? § Ex: Le gérant du magasin GAP veut commander des pantalons. § Tailles des clients du sondage § 30, 40, 32, 30, 40, 30, 32, 40, 40, 30, 40 § Quelle est la moyenne? § Quel est le mode? § S’il placer le nb. Minimum de commandes, devrait-il commander la taille moyenne?

Détermination du mode de données groupées par classes § Au lieu de calculer le mode on détermine la classe modale. § Exemple: tableau 5. 2 page 203 § Si on désire disposer d’une seule valeur, le milieu de classe modale peut servir de mode. § Faire exercice 5. 1 (page 203)

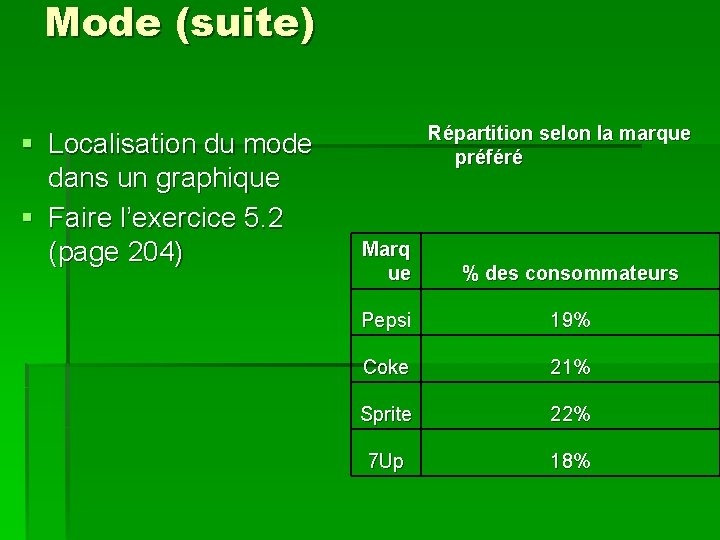
Mode (suite) § Localisation du mode dans un graphique § Faire l’exercice 5. 2 (page 204) Répartition selon la marque préféré Marq ue % des consommateurs Pepsi 19% Coke 21% Sprite 22% 7 Up 18%

Mode? § Exemple: tableau 5. 8 (page 207)

La médiane § § § Si on a un nb pair de données Ex: 1, 4, 3, 4, 5, 3, 2, 2, 3, 1 La médiane correspond à la moyenne de n/2 et (n/2)+1 § Que faire quand on a un tableau de fréquence? § Faire exercice 5. 4 (page 213)

Données groupées par classe § Méthode graphique (figure 5. 6 page 214) § Méthode analytique (tableau 5. 15 page 213) § Faire exercice 5. 5 (page 215)

La moyenne § Asymétrie nulle § Asymétrie positive: Quelques valeurs nettement supérieures aux autres. Déplacent la moyenne vers droite de la médiane. § Devoir § page 231, numéro 4, 5 (faire mode, médiane et moyenne), 7