Temporal Kohonen Map and the Recurrent SelfOrganizing Map

Temporal Kohonen Map and the Recurrent Self_Organizing Map Analytical and experimental Comparison Advisor: Dr. Hsu Graduate: Ching-Lung Chen 9/9/2020 IDSL, Intelligent Database System Lab 1

Outline • • • Motivation Objective Introduction The self-Organizing Map TKM & RSOM Comparison of TKM and RSOM Learning algorithms Conclusion Personal Opinion 9/9/2020 IDSL, Intelligent Database System Lab 2

Motivation • The basic SOM is indifferent to the ordering of the input patterns, but in real data is often sequential in nature. • The chain of the best matching units(bmus) for pattern sequences produce time varying trajectories of activity on the SOM 9/9/2020 IDSL, Intelligent Database System Lab 3

Objective • To compare two simple SOM based model that takes the temporal context of pattern into account is the Temporal Kohonen Map(TKM) and Recurrent Self-Organizing Map(RSOM). 9/9/2020 IDSL, Intelligent Database System Lab 4

Introduction (1/2) • The hierarchical model consists of two maps connnected with a leaky integrator memory: 1. The first of the maps transforms the input patterns and stored in the leaky integrator memory which preserves a trace of the past transforms. The content of the memory is the input of second map. 2. 9/9/2020 IDSL, Intelligent Database System Lab 5

Introduction (2/2) • The major difference between these hierarchical models is the computation of the content of the leaky memory connecting the first and the second map. • The TKM model was modified into the RSOM for better resolution, but it later turned out that the real improvement came from a consistent update rule for the network parameters. 9/9/2020 IDSL, Intelligent Database System Lab 6

The Self-Organizing Map(1/5) 1. Every point in the space is closer to the centroid of its region than to the centroid of any other region. 2. The centroids of the regions are defined by the weight vectors of the map. 3. Partitioning of this kind is called Vorionoi tessellation of the input space. 9/9/2020 IDSL, Intelligent Database System Lab 7

The Self-Organizing Map(2/5) • The target of the SOM approach is to minimize the sum of weighted errors between the input and the weight or the reference vectors. • w are the weight of unit i • The neighborhood function hi, j i 9/9/2020 IDSL, Intelligent Database System Lab 8

The Self-Organizing Map(3/5) • The neighborhood function is a Gaussian: • w are the map coordinates of the unit i. • s (n) is normally reduced as the learning progresses. i 9/9/2020 IDSL, Intelligent Database System Lab 9

The Self-Organizing Map(4/5) • Deriving an exact learning algorithm to minimize Eq(1) is difficult, so we ignore the discontinuities at the boundaries of the Voronoi cells, and can easily derive approximate learning rules. • Step 1 • Step 2 9/9/2020 IDSL, Intelligent Database System Lab 10

The Self-Organizing Map(5/5) • In the second step the weights can be updated with: • The neighborhood function is identical for samples with the same bmu we can rewire to 9/9/2020 IDSL, Intelligent Database System Lab 11

TKM & RSOM(1/4) TKM : max activity RSOM: min leaked difference vector 9/9/2020 IDSL, Intelligent Database System Lab 12

TKM & RSOM(2/4) • In TKM the activation of the unit is: • 0 <= d < 1 is a time constant • wi (n) is the weight vector of the unit I • X(n) is the input pattern • In the experiment , the weights were updated toward the last sample of the input sequence. 9/9/2020 IDSL, Intelligent Database System Lab 13

TKM & RSOM(3/4) • In RSOM the leaked quantity is the difference vector • yi (n, a ) is the leaked difference vector for unit i at step n • a is leaking coefficient analogous to the value of (1 -d ) • The RSOM the operator is moved from the unit outputs into the inputs. 9/9/2020 IDSL, Intelligent Database System Lab 14

TKM & RSOM(4/4) • After moving the leaky integrators into the difference vector computation we can treat the map much like the normal SOM when unit with: • An eerror function E(n) for the current sample x(n) • The stochastic weight update rule for Wi to minimize error E(n) is 9/9/2020 IDSL, Intelligent Database System Lab 15

Comparison of TKM and RSOM (1/7) • We derive the optimal or the activity maximizing weights for a set of sequences and a single unit for both TKM and RSOM. • The analysis directly extends to multiple units in the zero neighborhood case. 9/9/2020 IDSL, Intelligent Database System Lab 16

Comparison of TKM and RSOM (2/7) • When the maps share the same topology and data, the maximizing activity in TKM should lead to similar weights as minimizing the norm of the leaked difference vector in the RSOM • We first consider a single TKM unit and a set S = {X 1, X 2, …. , Xn} of sequences 9/9/2020 IDSL, Intelligent Database System Lab 17

Comparison of TKM and RSOM (3/7) • For the set S of sequences and weights w the activity U ( S , w. T ) over S is the sum T • U ( S , w. T ) is a parabola. Consequently its maximum lies either at its extreme or at the single zero of From 9/9/2020 IDSL, Intelligent Database System Lab 18

Comparison of TKM and RSOM (4/7) • We obtain • When all sequences have the same length n, the Equation (9) is constant allowing to simplify 9/9/2020 IDSL, Intelligent Database System Lab 19

Comparison of TKM and RSOM (5/7) • For the RSOM unit the leaked difference vector • Since the goal is to minimize the norm of the leaked difference vector, for the set S we can write 9/9/2020 IDSL, Intelligent Database System Lab 20

Comparison of TKM and RSOM (6/7) • For the error function at the optimum weights, parabola. From , which is minimized defines a • We obtain 9/9/2020 IDSL, Intelligent Database System Lab 21

Comparison of TKM and RSOM (7/7) • If we assume that all sequences have the same length n. We get: 9/9/2020 IDSL, Intelligent Database System Lab 22

Learning algorithms (1/8) • We show that generally the steady state weights of the TKM do not maximize the actiity and use simulations to show this affects the behavior of the TKM. • In a steady state the TKM weights have to be in the centroids of the last samples of the sequences in the Voronoi cells of the units. 9/9/2020 IDSL, Intelligent Database System Lab 23

Learning algorithms (2/8) • d=0 TKM activity for unit i in Eq(8) reduces to • and the corresponding steady state weights at are 9/9/2020 IDSL, Intelligent Database System Lab 24

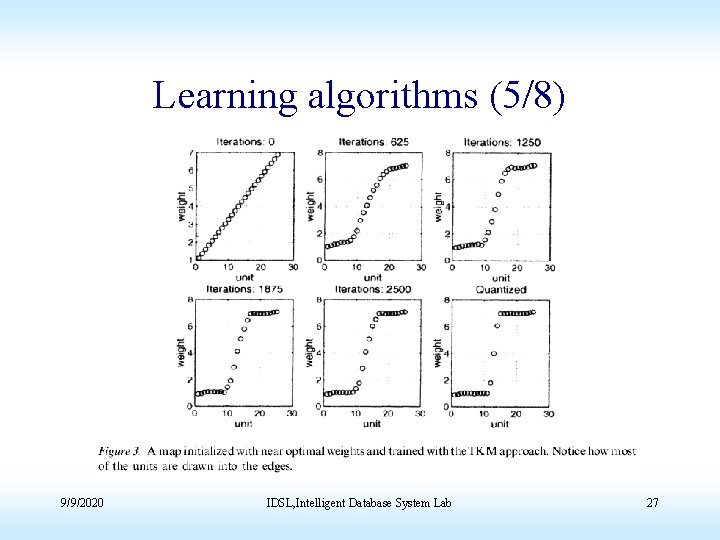
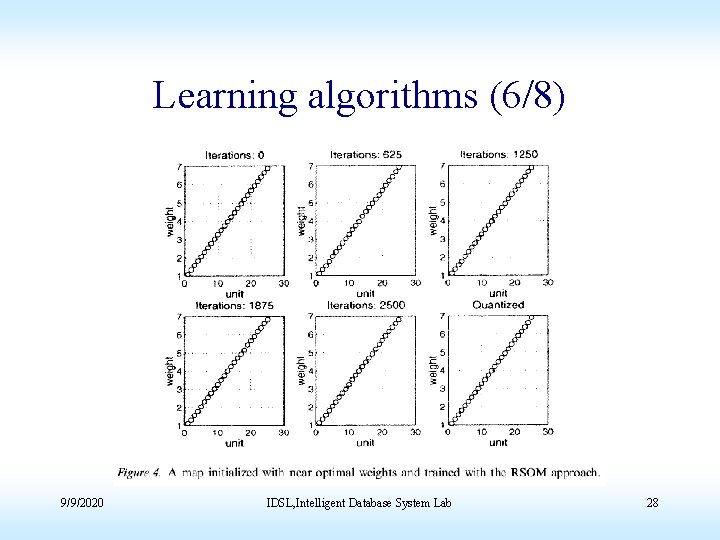
Learning algorithms (3/8) • We ran several simulations to show the impact of the discrepancy bewteen the bmu selection and the weight update in the TKM 9/9/2020 IDSL, Intelligent Database System Lab 25

Learning algorithms (4/8) 9/9/2020 IDSL, Intelligent Database System Lab 26

Learning algorithms (5/8) 9/9/2020 IDSL, Intelligent Database System Lab 27

Learning algorithms (6/8) 9/9/2020 IDSL, Intelligent Database System Lab 28

Learning algorithms (7/8) 9/9/2020 IDSL, Intelligent Database System Lab 29

Learning algorithms (8/8) 9/9/2020 IDSL, Intelligent Database System Lab 30

Conclusions • The analysis show that the RSOM allows simple derivation of an update rule that is consistent with the activity function of the model. • In a sense the RSOM provides a simple answer to the question regarding the optimal weights, but possibly at the cost of biological plausibility, which motivated the original TKM. • The RSOM approach has been applied in an experiment with EEG data. 9/9/2020 IDSL, Intelligent Database System Lab 31

Personal Opinion • Maybe we can use TKM or RSOM to experimental CIS with the bum produce time varying trajectories on the SOM. • I need read TKM or RSOM’s paper first then to study this paper. 9/9/2020 IDSL, Intelligent Database System Lab 32