Temperature and Heat Chapter 12 What is temperature

Temperature and Heat (Chapter 12) • What is temperature? - Is there a difference between heat and temperature? - What does it mean to say something is hot or cold? • Temperature of a body is a measure of the average kinetic energy of its constituent atoms. • Unlike heat (called thermal energy) temperature of a substance is not dependent on the type and number of atoms present (i. e. mass). • How can we define “hot” or “cold”? • Senses – Touch: can be very misleading… - Dissimilar objects (e. g. wood and metal) can feel warmer or colder even though both are at room temperature! • Temperature is really a comparative measurement to tell if an object is hotter or colder than something else.

Thermal Equilibrium • When two objects are in contact with each other for a long period of time, we say they are in thermal equilibrium. i. e. they both have the same temperature. • This is the basis for temperature (comparative) measurements. Thermometer • Invented by Galileo to indicate “degrees Thermoscope of hotness”. • As captured air in bulb is heated or cooled captured it expanded or contracted and liquid level scale air in bulb changed accordingly. • Thermometers tell us whether something liquid: is hotter or colder on an internationally water /wine? recognized reference scale. • Thermometer use: - fluid (liquid, gas) expansion - electrical resistance change; - changes in color…

Temperature Scales • Thermometers are based on reliable reference points such as freezing and boiling point of water. (Stable points as phase transition). • Want the reference points to be far apart – with a uniform scale in between. Fahrenheit scale (G. Fahrenheit, 18 th century) • He did not want to deal with negative values. So he set his “ 0” mark at the coldest temperature he could make in the laboratory (using mixture ice, water and salt). • He set his upper reference to human body temperature and called it 96 º (for easy division by half, quarter etc. ). • This resulted in scale (still in use in U. S. A. ) where freezing point of water = 32 ºF and boiling point = 212 ºF (at sea level). • There are 180 ºF between these two common reference points.

Celsius scale (A. Celsius, 18 th century) • He used freezing and boiling point of water for reference points and then divided the distance between them by 100 equal parts. • Strangely, he set the temperature of freezing water to 100 º and boiling water to 0 º! • Later revision resulted in the Celsius (or centigrade) scale with 100 degrees between reference points. • Each Fahrenheit degree is therefore smaller than a Celsius degree: 180 ºF = 100 ºC or 9 ºF = 5 ºC or 1°F = 59 °C Example: What is room temperature of 68 ºF in ºC? This is 36 ºF above freezing point of water (32 ºF). 36 ºF = 5 9 x 36 ºC = 20 ºC As 1 °F = 5 9 °C Thus: 68 ºF = 20 ºC

Conversion Between ºF and ºC Tc = 5 (Tf – 32) Tf = 9 5 Tc + 32 => 9 100 • i. e. multiplying Tc by 9 5 tells us how many degrees Fahrenheit above freezing. Example: At what temperature do the Celsius ºC and Fahrenheit scales have the same value? 20 Tf = 9 5 Tc + 32 0 set Tf = Tc to determine value… -40 Tf = 9 Tf + 32 5 or Tf = Tc = -40 º (F or C) • So when the temperature gets close to -40 º it does not matter which scale to use! • At higher and lower values they are quite different! 212 ºF 68 32 -40

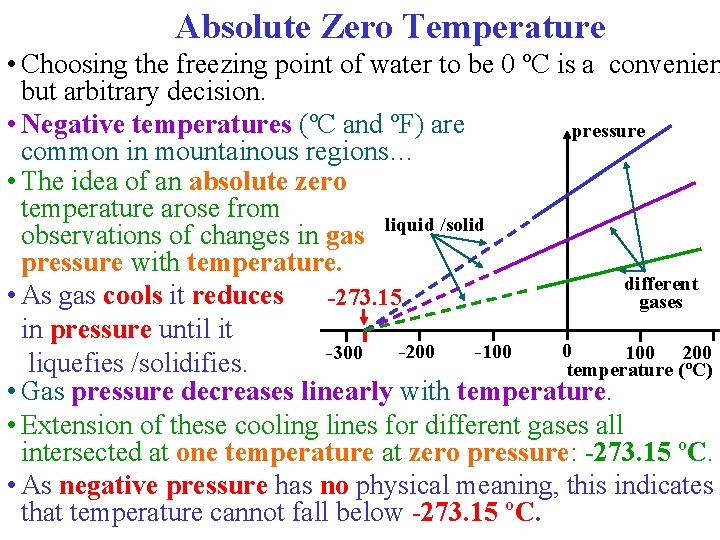
Absolute Zero Temperature • Choosing the freezing point of water to be 0 ºC is a convenien but arbitrary decision. • Negative temperatures (ºC and ºF) are pressure common in mountainous regions… • The idea of an absolute zero temperature arose from liquid /solid observations of changes in gas pressure with temperature. different • As gas cools it reduces -273. 15 gases in pressure until it 0 -100 -200 -300 100 200 liquefies /solidifies. temperature (ºC) • Gas pressure decreases linearly with temperature. • Extension of these cooling lines for different gases all intersected at one temperature at zero pressure: -273. 15 ºC. • As negative pressure has no physical meaning, this indicates that temperature cannot fall below -273. 15 ºC.

Kelvin Scales (after Lord Kelvin 19 th century) • The Kelvin (or absolute) scale has “ 0” at -273. 15 ºC • Uses the same degree intervals as Celsius scale. • To convert Celsius to Kelvin simply add 273. 15 T = Tc + 273. 15 • As Kelvin is an absolute scale, the comparative “degree” symbol is not used. Example 1: What is room temperature of 20 ºC in K? T = Tc + 273. 15 = 20 + 273. 15 = 293. 15 K (or 293 K) Example 2: Nitrogen (N 2) gas liquefies at 77 K. What is its temperature in ºC and ºF? Tc = T - 273. 15 = 77 - 273. 15 = -196. 15 ºC Tf = 9 5 Tc + 32 = 9 (-196. 15) + 32 = -321. 07 ºF 5

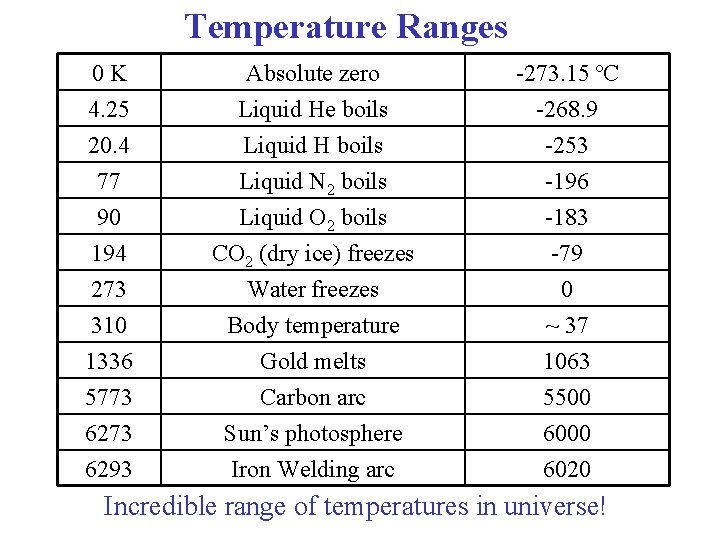
Temperature Ranges 0 K Absolute zero -273. 15 ºC 4. 25 20. 4 77 Liquid He boils Liquid H boils Liquid N 2 boils -268. 9 -253 -196 90 194 273 310 1336 5773 6293 Liquid O 2 boils CO 2 (dry ice) freezes Water freezes Body temperature Gold melts Carbon arc Sun’s photosphere Iron Welding arc -183 -79 0 ~ 37 1063 5500 6020 Incredible range of temperatures in universe!

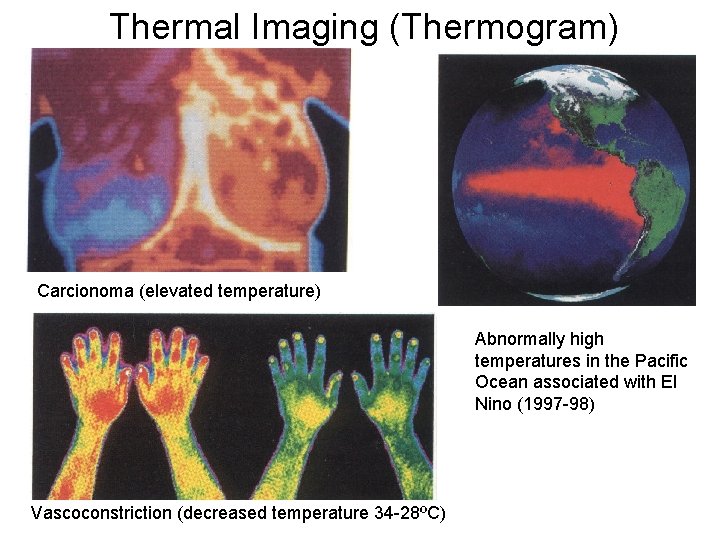
Types of Thermometers • Mercury thermometer: expansion of Hg in narrow tube (used for everyday temperature ranges). • Thermocouple: uses two different metals to generate a voltage between hot and cold junctions (range: -270 to 2300ºC) • Platinum resistance: electrical resistance increases with temperature (range: -270 to 700 ºC) • Thermal imaging (thermograph): all objects emit infra-red radiation. As temperature increases the infra-red intensity increases (used for a broad variety of applications).

Thermal Imaging (Thermogram) Carcionoma (elevated temperature) Abnormally high temperatures in the Pacific Ocean associated with El Nino (1997 -98) Vascoconstriction (decreased temperature 34 -28ºC)

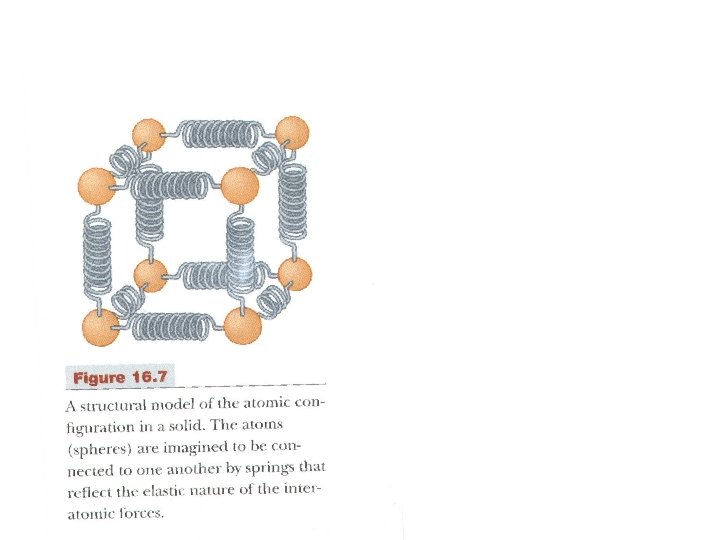
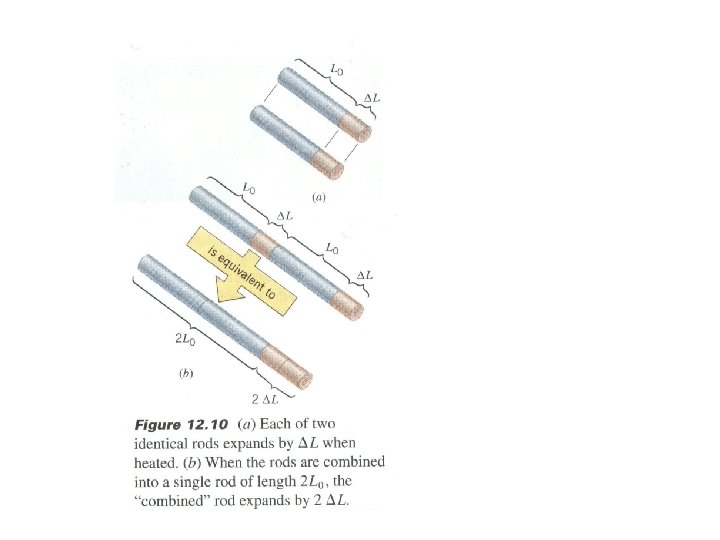
Thermal Expansion • An ancient knowledge – we all know that substances (solids, liquids, gases) expand when heated (and vice versa). Linear expansion: (rod, bar etc) • The change in length of a solid bar (ΔL) depends on: - change in temperature ΔT - original length L 0 - Coefficient of linear expansion, α ΔL = α. L 0. ΔT (where: ΔT in K or ºC) • Expansion occurs at the atomic level. As heat bar atoms vibrate with larger amplitude and their mean separations increase … This causes an expansion of the whole rod. • Objects continue to expand until they melt (change state). • ΔL expansion is a percentage variation - depends on original length L 0. • Example: 5% of 1 m = 0. 05 m, but 5% of 10 m = 0. 5 m

Coefficients of Thermal Expansion for Solids and Liquids (ºC)-1 Note: (β = 3α)

Thermal Expansion

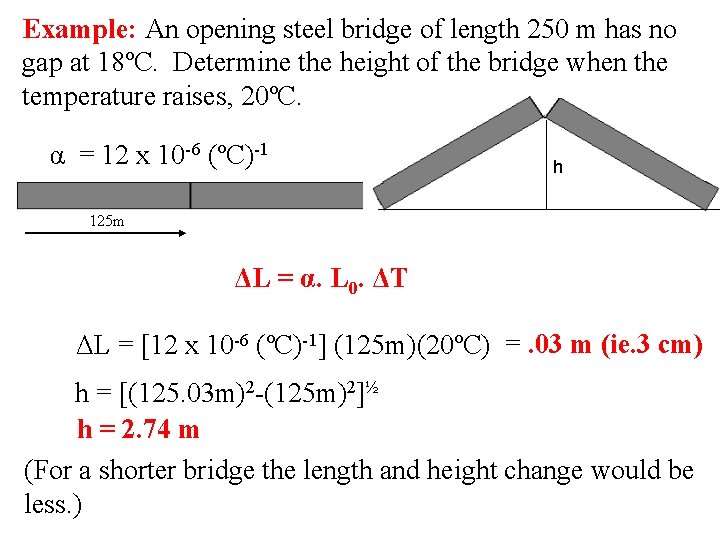
Example: An opening steel bridge of length 250 m has no gap at 18ºC. Determine the height of the bridge when the temperature raises, 20ºC. α = 12 x 10 -6 (ºC)-1 h 125 m ΔL = α. L 0. ΔT ΔL = [12 x 10 -6 (ºC)-1] (125 m)(20ºC) =. 03 m (ie. 3 cm) h = [(125. 03 m)2 -(125 m)2]½ h = 2. 74 m (For a shorter bridge the length and height change would be less. )

Expansion of Holes • What happens to the size of a hole when a material with a hole in it expands? • When the individual tiles expand, the hole also expands! • The expanded hole is the same size as the heated tile. • Result: A hole (of any shape) in a solid material, therefore expands or contracts just as if it were made of the material that surrounds it. Volumetric expansion (Solids and liquids): • Analogous to linear expansion, volumetric expansion: ΔV = β. V 0. ΔT (Note: β ≈ 3 times α for solids).

Temperature Extremes • Highest temperature likely to exist occur at center of certain stars, T ~ 4 x 109 K (a theoretical extreme). • At ~1010 K matter will fragment into subatomic particles! • A hydrogen bomb ignites at ~ 4 x 107 K and blazes to 108 K! • Center of Sun only 1. 5 x 107 K (15 million K) • Atoms (matter) is formed within stars at >105 K. • Liquid helium (4. 25 K) is most exotic of all cryogenic materials. • Liquid He can be cooled (by pumping) to 2. 18 K where it undergoes a dramatic change – not a solid but a superfluid with wonderful properties: superconductivity. • Lowest temperature achieved ~2 x 10 -8 K! • At such temperatures atoms almost stationary? But He still a liquid (zero point energy).

Bimetallic Strip • Made of two strips of metal joined together but having different coefficients of linear expansion. • Often brass (α = 19 x 10 -6 ºC -1) and steel (α = 12 x 10 -6 ºC -1) are used. • When heated (cooled) the brass expands (contracts) more than the steel and the strip bends. • Bimetallic strips frequently used in electrical switches to automatically adjust temperature.

• Expansion is usually quite small – typical metals expand about 7% when temperature rises from near 0 K to its melting point. • Most materials have a positive coefficient of linear expansion (except rubber under tension shrinks!) • Coefficient α depends on atomic structure. E. g. lead is a soft metal that is easily melted and its atoms are less tightly bound. It therefore has a high coefficient of expansion (29 x 10 -6 K-1). • In comparison, Pyrex glass has very low value of α (3 x 10 -6 K -1) and quartz even lower (about 50 x less than lead). Result: Buckled railroad track if rails too long. • Now we use very low expansion steel alloy to stop buckling of continuous track. Volumetric expansion (Solids and liquids): • Analogous to linear expansion, volumetric expansion: ΔV = β. V 0. ΔT (Note: β ≈ 3 times α for solids).

• Liquids are not bound like solids and their volume coefficient of expansion is much larger (around 50 times) that of a solid volume. • (Note: Both α and β are dependent on temperature as well. ) Results: • Bimetal strip bends when heated – used for thermal sensor switches, car indicators… • Bridges expand in summer (and vice versa) – need expansion joints. E. g. Bay bridge in San Francisco contracted 1. 3 m in 1937! • Dental fillings have same coefficient of expansion as teeth to stop them cracking! • Loosening metal lids on glass jars – metal expands more than glass when warmed.

Temperature and Heat • Temperature of a body is a measure of the average kinetic energy of its constituent atoms. • Temperature of a substance is not dependent on the type and number of atoms present (i. e. mass). In contrast: • Heat (thermal energy) of a body is a measure of the total net K. E. possessed by the constituent atoms /molecules in motion. • The thermal energy depends on the total number of atoms present and on their average K. E. (i. e. temperature). Example 1: The thermal energy (heat) stored in the Atlantic Ocean is enormous but the average K. E. of its molecules is low and hence its temperature is low. Example 2: In nuclear reactions the temperature of a gas can be millions of degrees but its mass is very low and hence its heat content is low.