TEMARIO MATRICES ELEMENTOS DE UNA MATRIZ 2 3

TEMARIO MATRICES • ELEMENTOS DE UNA MATRIZ ……………………. . . 2 3 • EJEMPLOS DE MATRICES ……………………… 4 • DEFINICIÓN ……………………………. . 5 6 SUBMATRIZ Y COFACTORES ……………………. 7 OBTENCIÓN DE DETERMINANTE MEDIANTE COFACTORES 8 MATRICES TRIANGULADAS………………. . …………… 9 CLASES DE MATRICES ………………. 10 OPERACIONES (Suma Resta y multiplicación por un escalar ) ……………. 11 PRODUCTO DE MATRICES ………………………. 12 PRODUCTOS ESPECIALES …………………. . ……… 13 • DETERMINANTE DE UNA MATRIZ …………………. • • MATRICES ESPECIALES ………………. 14 15 16 LA MATRIZ INVERSA, PROPIEDADES, MÉTÓDOS ……. . 17 18 19 METODOS PARA OBTENER LA INVERSA ………. . • DEFINICIÓN MATRÍS ADJUNTA O DE COFACTORES ………. . • •

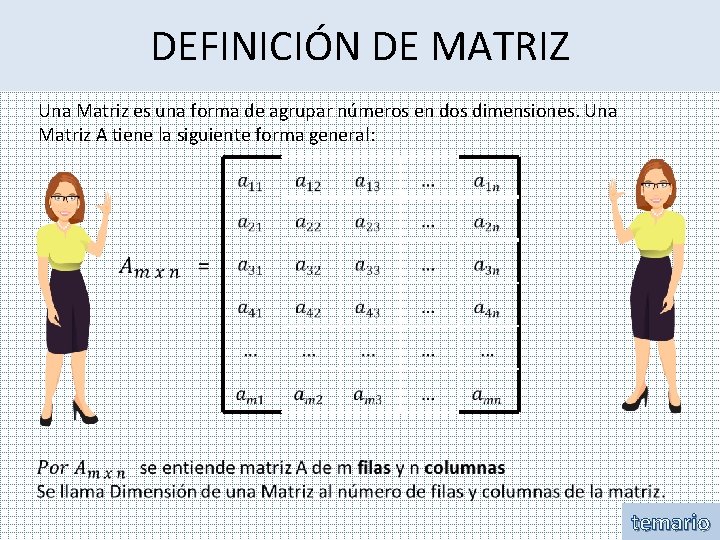
DEFINICIÓN DE MATRIZ Una Matriz es una forma de agrupar números en dos dimensiones. Una Matriz A tiene la siguiente forma general: temario

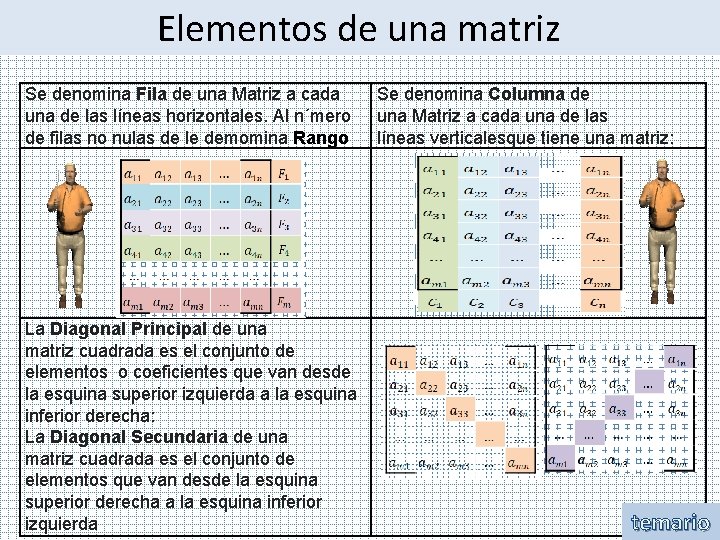
Elementos de una matriz Se denomina Fila de una Matriz a cada una de las líneas horizontales. Al n´mero de filas no nulas de le demomina Rango La Diagonal Principal de una matriz cuadrada es el conjunto de elementos o coeficientes que van desde la esquina superior izquierda a la esquina inferior derecha: La Diagonal Secundaria de una matriz cuadrada es el conjunto de elementos que van desde la esquina superior derecha a la esquina inferior izquierda Se denomina Columna de una Matriz a cada una de las líneas verticalesque tiene una matriz: temario

Ejemplos de matrices • temario

Determinante de una Matriz Para una matriz de 3 3, Regla de Sarrus: diferencia entre las suma de los productos de las diagonales de izquierda a derecha con las sumas de los productos de las diagonales de derecha izquierda , que se forman al repetir a continuación de la matriz las dos primeras filas temario

Submatriz o Menores y cofactores • Nota: los cofactores se utilizas por ejemplo para el cálculo de determinantes, la obtención de la Matriz Adjunta, y la Matriz Inversa temario

OBTENCIÓN DE DETERMINANTE MEDIANTE COFACTORES • Pasos 1) Se elige una fila o columna 2) Se identifica los elementos de la fila o columna elegida 3) Se calculan los cofactores de esa fila o columna 4) Se suman los productos de cada elemento de esa fila o columna con su correspondiente cofactor temario

Matrices triangulares Matriz Triangular Superior Matriz Triangular Inferior Una Matriz Triangular Superior es aquella matriz cuadrada cuyos valores por debajo de la diagonal principal son todos iguales a 0 Una Matriz Triangular Inferior es aquella matriz cuadrada cuyos valores por encima de la diagonal principal son todos iguales a 0 A una matriz se la puede triangular a través de las Transformaciones Elementales que consiste en: «Reemplazar una fila por un múltiplo de la misma o sumándole a la fila o un múltiplo de la que se quiere modificar un múltiplo de otra de sus filas» temario

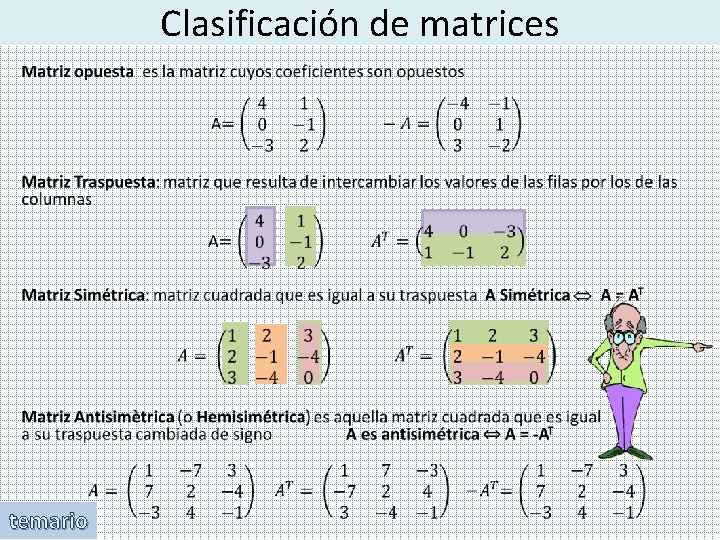
Clasificación de matrices • temario

OPERACIONES CON MATRICES • temario

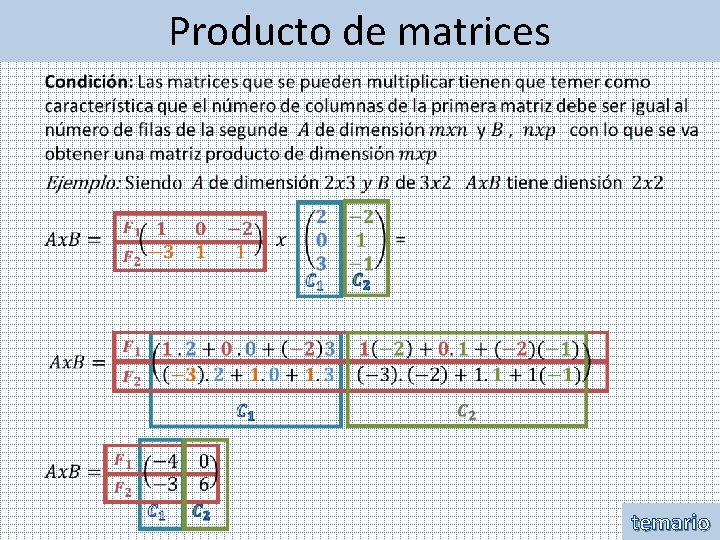
Producto de matrices • temario

Multiplicaciones especiales El producto de dos matrices Diagonal da una matriz diagonal. El producto de dos matices trianguladas superiormente da una matriz también triangulada superiormente temario

MATRICES ESPECIALES Matriz Idempotente: matriz que multiplicada por si misma da como resultado la misma matriz Matriz Involutiva: matriz que multiplicada por si misma da como resultado la matriz unidad o identidad Matriz Ortogonal: matriz que multiplicada por su traspuesta resulta la matriz identidad A es idempotente ⇔ A · A = A A es involutiva ⇔ A · A = I A es Ortogonal ⇔ A · AT = I temario

Matriz Adjunta • temario

Matriz Inversa • temario

PROPIEDADES DE LA MATRIZ INVERSA La inversa de la inversa es la matriz de origen: (A-1)-1 = A La inversa de un producto de matrices es igual al producto de las inversas de las matrices pero cambiado de signo: (A · B)− 1 = B− 1 · A− 1 Sea una matriz invertible, entonces la inversa de su traspuesta es igual a la traspuesta de la inversa: (AT)-1 = (A-1)T Las matrices inversas se calculan como el adjunto de la matriz entre su determinante (si este es distinto de cero): (A)-1 = Adj (A) / |A| https: //www. matesfacil. com/calculadoras/matrices/calculadora-online-matrizinversa-adjunta-2 x 2 -3 x 3 -matrices. html temario

• temario

Matriz inversa usando la Matriz Adjunta • Obtener el valor del determinante Obtener los cofactores de la Matriz Inversa matriz Adjunta Nota el determinante de la matriz tiene que ser distinto de 0 temario

Matriz inversa por método de Gaus Por medio de Transformaciones elementales, vamos modificando nuestra matriz hasta obtener la matriz identidad. Cada paso que apliquemos a la matriz se lo aplicaremos a la matriz identidad. Cuando hayamos obtenido la matriz identidad, la derecha será la inversa. Si no podemos llegar a la matriz identidad (por ejemplo, sale alguna fila de ceros), significa que la matriz no será inversible. Por medio de transformaciones elementales, vamos modificando nuestra matriz hasta obtener la matriz identidad. Cada paso que apliquemos a la matriz se lo aplicaremos a la matriz identidad. Cuando hayamos obtenido la matriz identidad, la derecha será la inversa. Si no podemos llegar a la matriz identidad (por ejemplo, sale alguna fila de ceros), significa que la matriz no será inversible. Ejemplo con una matriz de dimensión 2 x 2

FIN