TEMA VI ESQUEMA GENERAL Consideraciones generales Diseo de

TEMA VI

ESQUEMA GENERAL Consideraciones generales Diseño de bloques de grupos al azar. Modelo estructural y componentes de variación Diseño de Cuadrado Latino. Modelo estructural y componentes de variación Diseño jerárquico al azar. Modelo estructural y componentes de variación DISEÑOS EXPERIMENTALES MULTIGRUPO OPTIMIZADOS

Concepto El principal objetivo de la experimentación es el control de las fuentes de variación extrañas. La neutralización o control de las variables extrañas incide directamente en la reducción de la variación del error. Es decir, las unidades varían con respecto a cualquier variable a excepción de la controlada. Siendo esto así, el margen de variación es menor que con la presencia de la variable extraña (o variable no controlada). . . //. .

Desde la lógica de la experimentación, una técnica ideal consiste en eliminar los factores extraños. Ese ideal es imposible de conseguir, particularmente en contextos de investigación social como conductual. Por esta razón, se han desarrollado unos procedimientos que, asociados a la propia estructura del diseño, permiten controlar una o más variables extrañas y neutralizar su acción sobre la variable dependiente.

Diseño de bloques de grupos al azar

Técnica de bloques Mediante la técnica de bloques se pretende conseguir una mayor homogeneidad entre los sujetos o unidades experimentales intra bloque y una reducción del tamaño del error experimental. La formación de bloques homogéneos se realiza partir de los valores de una variable de carácter psicológico, biológico o social, altamente relacionada con la variable dependiente. . . //. .

Al mismo tiempo, la presencia del azar queda garantizada ya que, dentro de los bloques, las unidades son asignadas aleatoriamente a las distintas condiciones experimentales. Cada condición representa un nivel o tratamiento de la variable independiente.

Diseño de bloques de grupos al azar Con la técnica de bloques se consigue una mayor homogeneidad entre los sujetos o unidades experimentales intra bloque y una reducción del tamaño del error experimental. La formación de bloques homogéneos se realiza partir de los valores de una variable de carácter psicológico, biológico o social, altamente relacionada con la variable dependiente. . . //. .

Al mismo tiempo, la presencia del azar queda garantizada ya que dentro de los bloques las unidades son asignadas aleatoriamente a las distintas condiciones experimentales. Cada condición representa un nivel o tratamiento de la variable independiente.

Clasificación

Diseño de bloques de grupos completamente al azar Diseño de un solo sujeto por casilla Diseño de dos o más sujetos por casilla

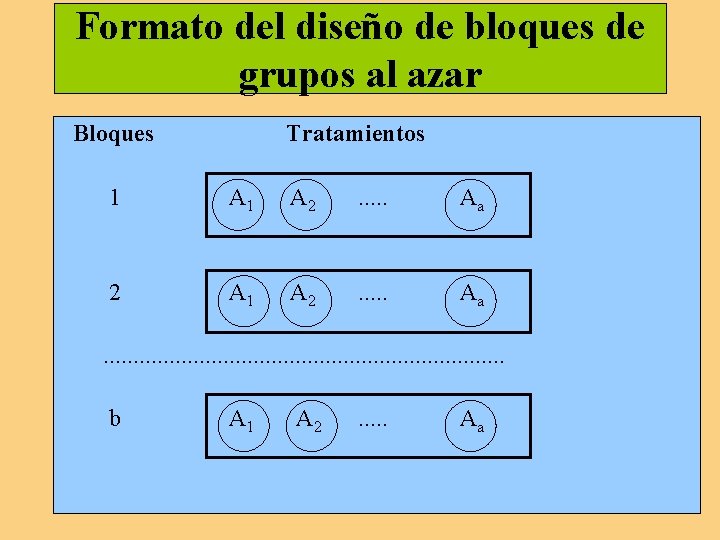
Formato del diseño de bloques de grupos al azar Bloques Tratamientos 1 A 1 A 2 . . . Aa 2 A 1 A 2 . . . Aa . . . . b A 1 A 2 . . . Aa

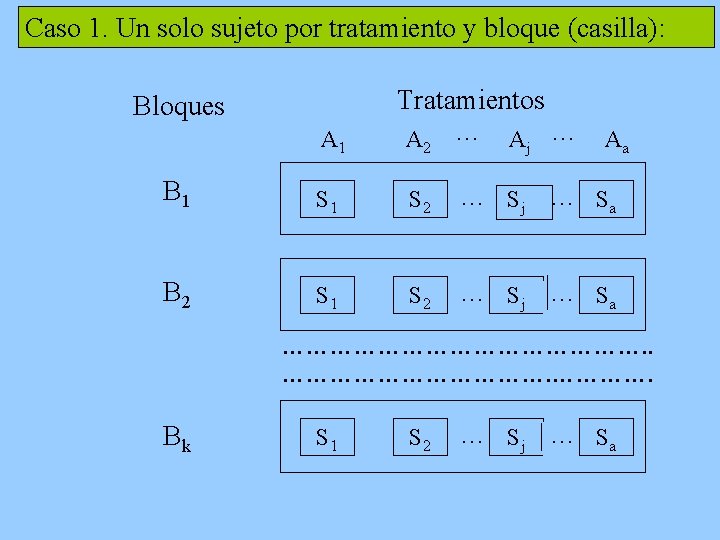
Caso 1. Un solo sujeto por tratamiento y bloque (casilla): Tratamientos Bloques A 1 A 2 ··· Aj ··· Aa B 1 S 2 ··· Sj ··· Sa B 2 S 1 S 2 ··· Sj ··· Sa ……………………. Bk S 1 S 2 ··· Sj ··· Sa

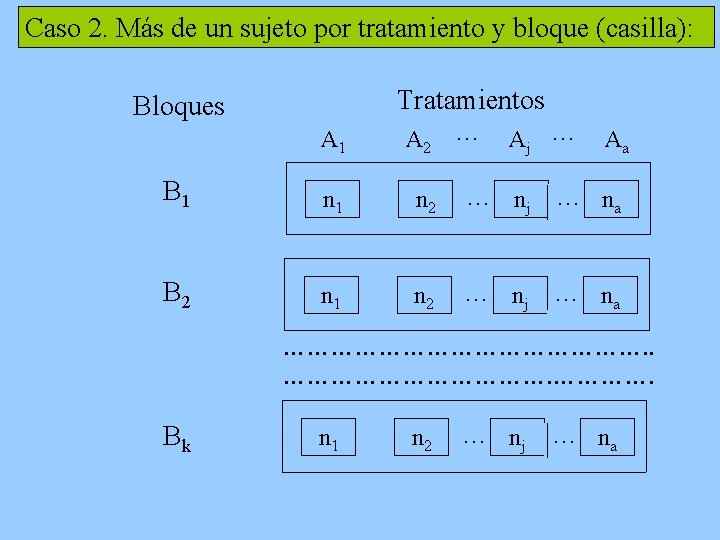
Caso 2. Más de un sujeto por tratamiento y bloque (casilla): Tratamientos Bloques A 1 A 2 ··· Aj ··· Aa B 1 n 2 ··· nj ··· na B 2 n 1 n 2 ··· nj ··· na ……………………. Bk n 1 n 2 ··· nj ··· na

Ventajas de la técnica de bloques Según Baxter (1940), son notorias las ventajas del diseño de bloques en investigación psicológica al neutralizarse una potencial fuente de variación extraña que, en caso contrario, incrementaría la variación del error. En psicología, la mayoría de las fuentes de variación extrañas, directamente asociadas a la heterogeneidad de los datos, se derivan de las diferencias interindividuales. En consecuencia, son variables de sujeto que no sólo distorsionan la acción de los tratamientos sino que también incrementan las diferencias entre las unidades. . . //. .

Mediante la técnica de bloques se consigue un material experimental mucho más homogéneo, se reduce la magnitud del error experimental y se incrementa el grado de precisión del experimento.

Modelos ANOVA del diseño Modelo aditivo: un sujeto por casilla Yijk = µ + j + ßk + ijk (1) Modelo no aditivos: dos o más sujetos por casilla Yijk = µ + j + ßk + ( ß)jk + ijk (2)

MODELO ESTRUCTURAL DEL AVAR: DISEÑO DE BLOQUES n=1 n>1

Sobre los modelos El modelo aditivo asume que la interacción de tratamientos por bloques es nula y, en consecuencia, que el dato es explicado por la combinación lineal de los componentes de ecuación anterior. Cuando no se cumple el supuesto de aditividad, el efecto cruzado o componente de no aditividad (interacción de las condiciones experimentales con los bloques) se convierte en una fuente de variación extra, es decir, el efecto de la combinación de tratamientos por bloques ha de añadirse a los efectos ya presentes en el modelo. . . //. .

En ausencia de interacción, se aplica el modelo aditivo sin problema alguno. Ahora bien, cuando los sujetos de un determinado bloque responden a los tratamientos de forma diferente a como responden los sujetos de otro bloque, cabe la posibilidad de una interacción de bloques por tratamientos. . . //. .

Puesto que, de otra parte, el modelo de la ecuación 1 no refleja ese efecto combinado, y puesto que la variabilidad de este componente no es absorbida ni por la Suma de Cuadrados de tratamientos, ni por la Suma de Cuadrados de bloques, el efecto combinado pasa a engrosar el término de error. En ese caso, el término de error no sólo contiene la variabilidad debida al muestreo, sino también la variabilidad debida al efecto de la interacción. Y dado que con interacción se incrementa o sesga positivamente el término de error, cabe esperar que el valor F sea negativamente sesgado. De esta forma, se incrementa la dificultad de detectar el efecto de los tratamientos.

Diseños de bloques aleatorizados (n=1)

Ejemplo práctico Un investigador pretende estudiar la efectividad de tres métodos distintos en la enseñanza de las matemáticas: método tradicional (A 1), método de programación (A 2), y método audio-visual (A 3), para un determinado nivel escolar. Desde la perspectiva experimental, el problema podría resolverse formando tres grupos al azar de sujetos, uno para cada método. Al finalizar el estudio, se pide a los sujetos del experimento que resuelvan un total de 10 problemas de cálculo matemático. La resolución de esos problemas de matemáticas es una medida de ejecución que evalúa la efectividad de los métodos de enseñanza. . . //. .

Ahora bien, como ocurre con la mayoría de investigaciones del ámbito educativo, se considera que el nivel intelectual de los escolares es una probable variable extraña capaz de contaminar los resultados del experimento. Para controlar esa variable, mediante la estructura de diseño, se elige un diseño de bloques de grupos al azar.

Procedimiento El experimento se resuelve de la siguiente forma: en primer lugar, se forman 10 bloques con base a los valores de la variable Cociente Intelectual (CI). Cada bloque representa un determinado cociente intelectual, lo cual requiere la selección previa de los sujetos. Así, para cada valor de CI se eligen tres sujetos o unidades del bloque. De esta forma, la variación de los sujetos intra-bloque es menor que la de todos los sujetos de la muestra.

En segundo lugar, las unidades de los bloques se asignan al azar a los tratamientos de modo que, dentro del bloque, cada sujeto recibe un tratamiento distinto. Según este procedimiento, sólo se dispone de un sujeto por casilla o combinación de bloque por tratamiento. Así, cada bloque constituye una réplica entera del experimento.

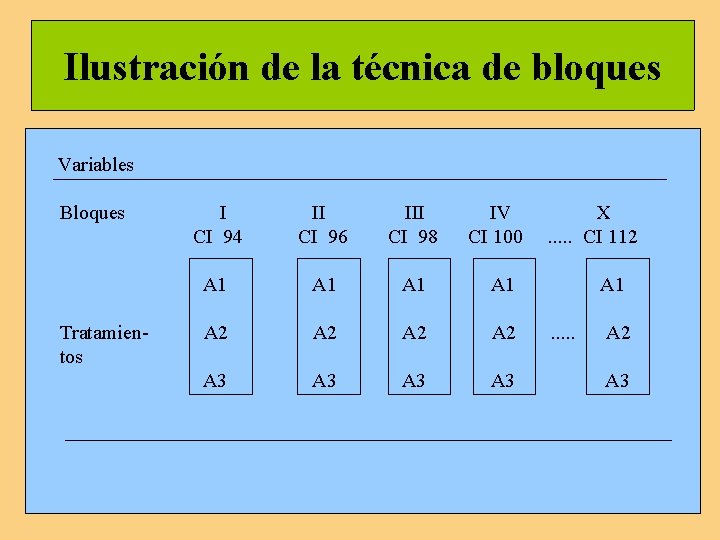
Ilustración de la técnica de bloques Variables Bloques III IV X CI 94 CI 96 CI 98 CI 100 . . . CI 112 A 1 A 1 Tratamien- A 2 . . . A 2 tos A 3 A 3

Modelo de prueba estadística Paso 1. Se asume, por hipótesis de nulidad, que las medias de los grupos experimentales proceden de una misma población y que, por consiguiente, son iguales: H 0: µ 1 = µ 2 = µ 3 Paso 2. En la hipótesis alternativa se especifica que, por lo menos, hay una diferencia entre las medias de los tres tratamientos. En términos estadísticos, se tiene: H 1: por lo menos una desigualdad

Paso 3. Se elige, como prueba estadística, el Análisis de la Variancia (ANOVA), asumiendo el modelo aditivo y un nivel de significación de = 0. 05. Paso 4. Realizado el experimento, se obtiene la matriz de datos del diseño. A partir de estos datos, se calculan las variancias para estimar el valor empírico de F, asumiendo el modelo de aditividad.

DISEÑO DE BLOQUES (n=1) N. Bloque 1 2 3 4 5 6 7 8 9 10 TOTALES MEDIAS TRATAMIENTOS A 1 A 2 A 3 TOTAL POR BLOQUE 6 7 8 21 7 6 7 20 4 8 9 21 5 9 7 21 7 5 8 20 3 4 10 17 5 6 7 18 8 8 9 25 7 7 10 24 6 5 7 18 58 65 82 205 5. 8 6. 5 8. 2 6. 83

Modelo anova aditivo Yijk = µ + j + ßk + ijk se presupone que cada dato u observación (Yijk) es una combinación aditiva de la media total del experimento (µ), el efecto de un determinado tratamiento ( j), el efecto de un bloque específico (ßk) y el componente de error ( ijk).

Cálculo de las Sumas de Cuadrados En función del modelo estructural de análisis, se divide la Suma de Cuadrados total en los siguientes componentes aditivos: Suma de Cuadrados de tratamientos, Suma de Cuadrados de bloques y Suma de Cuadrados del error. SCtotal = SCtrat. + SCbloq. + SCerror

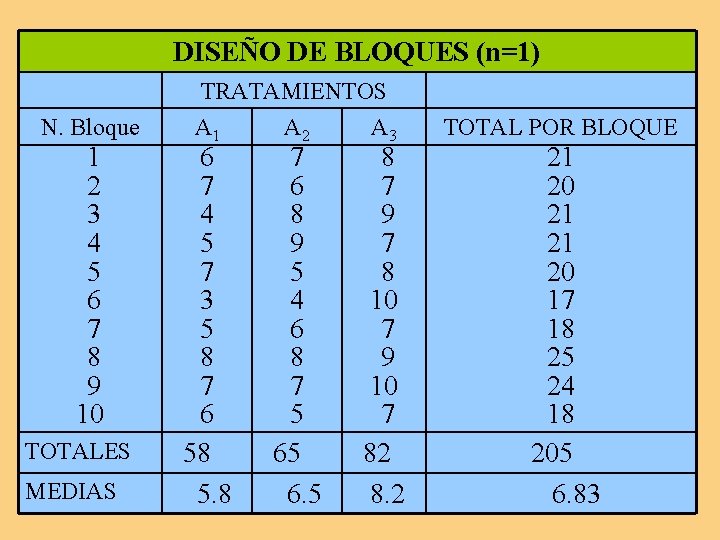
SCtotal = [(6)² + (7)² +. . . + (7)²] – [(205)²/30] = 88. 16 SCtrat. = [(58)²/10 + (65)²/10 + (82)²/10] – [(205)²/30] = 30. 47 SCbloq. = [(21)²/3 + (20)²/3 +. . . + (18)²/3] – [(205)²/30] = 19. 50 SCerror = SCtotal - SCtrat. - SCbloq. = 88. 16 - 30. 47 - 19. 5 = 38. 19

CUADRO RESUMEN DEL AVAR: DISEÑO DE BLOQUES (n=1) F. V. SC g. l CM Trat (A) Bloques (B) Error (Ax. B) 30. 47 (a-1)=2 15. 23 19. 50 (b-1)=9 2. 16 38. 19 (a-1)(b-1)=18 2. 12 Total (T) 88. 16 ab-1=29 F 0. 95(2/18) = 3. 55; F 0. 95(9/18) = 2. 46 F p 7. 18 1. 02 <0. 05 >0. 05

Modelo de prueba estadística Paso 5. Dado que el valor observado de F es menor que el teórico, a un nivel de significación de 0. 05, se infiere que hay una diferencia significativa entre los tratamientos. Por otra parte, es posible probar la hipótesis sobre los bloques. . . //. .

La hipótesis a probar, H 0: ß 1 = ß 2 =. . . = ß 10, tiene como término de contraste la variancia del error. Del análisis se concluye la no diferencia, estadísticamente hablando, entre los bloques y se acepta, en consecuencia, la hipótesis de nulidad.

Diseños de bloques aleatorizados (n>1)

Ejemplo práctico A partir del experimento descrito, a raíz del diseño de bloques de un sólo sujeto por casilla, considérese que hay tres sujetos por casilla. Así, se tiene un total de nueve sujetos por bloque y tres sujetos por tratamiento intrabloque.

Modelo de prueba estadística Paso 1. Se definen tres hipótesis de nulidad para los efectos de tratamientos, bloques e interacción. En términos de efectos, esas hipótesis de nulidad son: H 0: 1 = 2 = 3 = 0 H 0: ß 1 = ß 2 =. . . = ß 10 = 0 H 0: aß 11 = aß 12 =. . . = aß 310 = 0

Paso 2. La primera hipótesis alternativa coincide con la hipótesis experimental o hipótesis de efecto de tratamientos, la segunda se refiere al efecto de la variable de bloques y, por último, la tercera recoge el efecto de la interacción entre tratamientos y bloques. Las tres hipótesis alternativas toman la misma expresión. H 1: por lo menos una desigualdad

Paso 3. La prueba estadística se basa en el Análisis de la Variancia (F de Snedecor), asumiendo el modelo estructural o de efectos propuesto y un nivel de significación de = 0. 05. Paso 4. Realizado el experimento, se obtiene la matriz de datos del diseño. Con estos datos, se estiman las variancias para calcular el valor empírico de F.

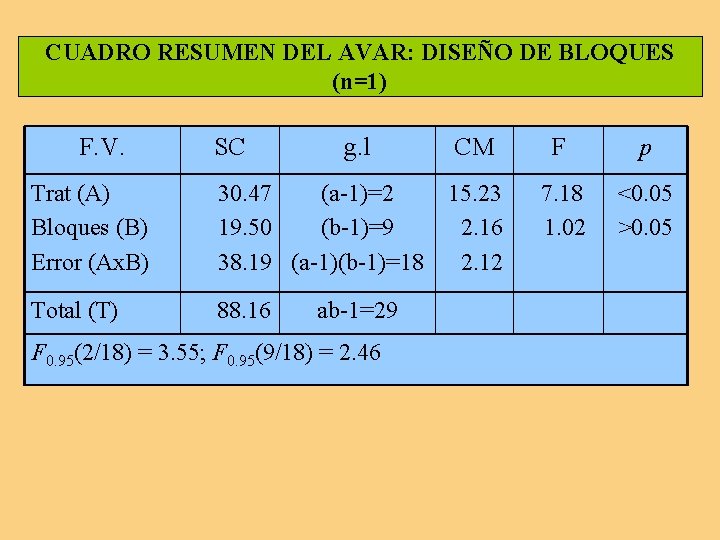
DISEÑO DE BLOQUES (n>1) TRATAMIENTOS A 2 A 3 N. Bloque A 1 1 2 3 4 5 6 7 8 9 10 6, 5, 3 (14) 7, 5, 4 (16) 3, 5, 4 (12) 6, 5, 5 (16) 7, 5, 8 (20) 5, 3, 4 (12) 6, 4, 5 (15) 7, 6, 9 (22) 6, 8, 7 (21) 7, 6, 7 (20) 168 TOTALES 6, 7, 5 (18) 5, 6, 5 (16) 7, 6, 7 (20) 8, 7, 9 (24) 5, 4, 7 (16) 5, 6, 4 (15) 7, 6, 5 (18) 8, 7, 9 (24) 6, 9, 6 (21) 5, 6, 4 (15) 187 TOTAL POR BLOQUE 7, 6, 9 (22) 54 7, 4, 6 (17) 49 9, 10, 7 (26) 58 7, 8, 6 (21) 61 9, 10, 7 (26) 62 10, 9, 8 (27) 54 8, 6, 5 (19) 52 9, 10, 7 (26) 72 8, 10, 9 (27) 69 6, 8, 7 (21) 56 232 587

Modelo anova no aditivo Yijk = µ + j + ßk + ( ß)jk + ijk donde Yijk es cualquier dato u observación del experimento, µ la media total del experimento, j el efecto de un determinado nivel de tratamiento, ßk el efecto de un determinado bloque, ( ß)jk el efecto cruzado o efecto de la casilla, y ijk el error experimental. Por lo general, este modelo es de efectos fijos tanto para la variable de tratamiento como para la variable de bloques.

Cálculo de las Sumas de Cuadrados SCtotal = SCtrat. + SCbloq. + SCtrat. xbloq. + SCerror SCtotal = [(6)² + (7)² +. . . + (7)²] – [(587)²/90] = 276. 46 SCtrat. = [(168)²/30 + (187)²/30 + (232)²/30] – [(587)²/90] = 72. 03 . . //. .

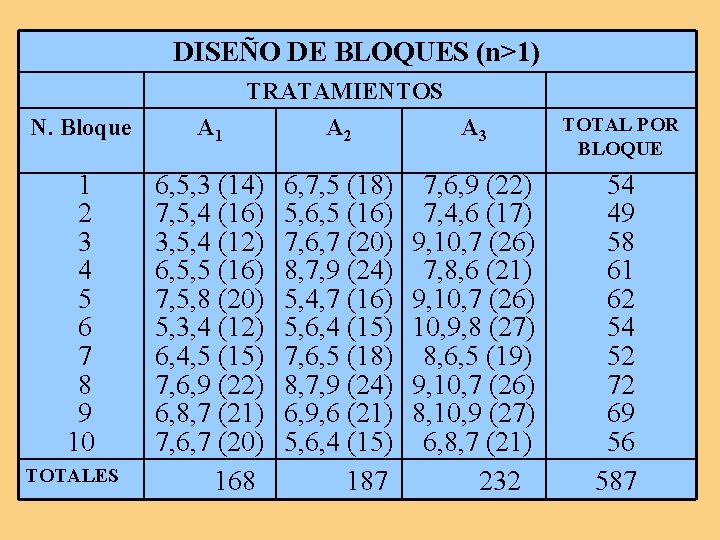
SCbloq. = [(54)²/9 + (49)²/9 +. . . + (56)²/9] – [(587)²/30] = 54. 46 SCtrat. xbloq. = SCgrupos - SCtrat. - SCbloq. = [(14)²/3 + (16)²/3 +. . . + (21)²/3] – [(587)²/90] – 72. 03 – 54. 46 = 61. 97 SCerror = SCtotal – SCtrat. – SCbloq. – SCtrat. xbloq. = 88. 00

CUADRO RESUMEN DEL AVAR: DISEÑO DE BLOQUES (n>1) F. V. SC g. l CM Trat (A) 72. 03 (a-1)=2 36. 01 Bloques (B) 54. 46 (b-1)=9 6. 05 Inter (Ax. B) 61. 97 (a-1)(b-1)=18 3. 44 Error (S/Ax. B) 88 ab(n-1)=60 1. 47 Total (T) 276. 46 F p 24. 50 4. 11 2. 34 <0. 05 abn-1=89 F 0. 95(2/60) = 4; F 0. 95(9/60) = 2. 04; F 0. 95(18/60) = 1. 786

Modelo de prueba estadística Paso 5. Dado que los valores observados de F son más grandes que los teóricos, al nivel de significación de 0. 05, se infiere la no-aceptación de las tres hipótesis nulas y que, por tanto, son significativos los efectos asociados a las distintas fuentes de variación.

Fin diseños de bloques

Diseño de Cuadrado Latino

Diseño de Cuadrado Latino El diseño de Cuadrado Latino es un plan experimental donde cada tratamiento sólo aparece una vez en cada fila y en cada columna. Asimismo, el Cuadrado Latino siempre requiere, por definición, tres dimensiones de variación a d niveles cada una. Los Cuadrados Latinos se representan tradicionalmente por tablas d x d, con letras en las casillas para simbolizar los niveles de la variable de tratamiento.

Según Dowley y Wearden (1991), los diseños de Cuadrado Latino son formatos económicos porque no requieren todas las combinaciones posibles entre las tres dimensiones de variación. Así, a título de ejemplo, el formato de Cuadrado Latino 3 x 3 se representa en la tabla siguiente.

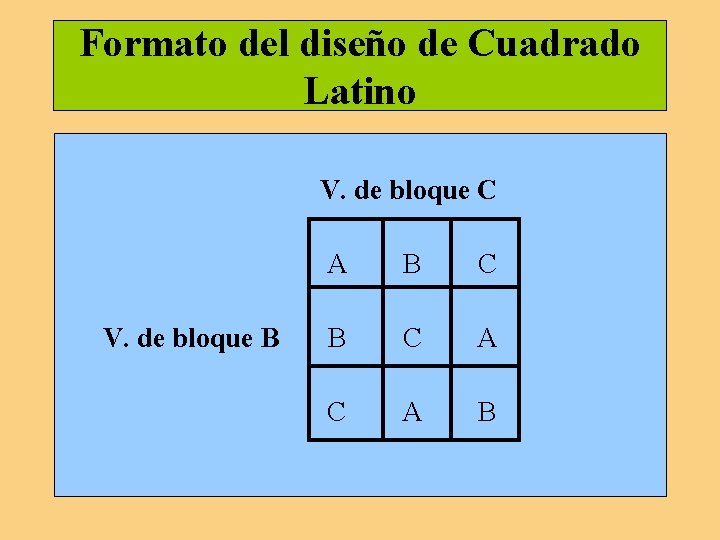
Formato del diseño de Cuadrado Latino V. de bloque C A B C V. de bloque B B C A B

Cuadrado Latino y bloques Las filas (variable B) y las columnas (variable C) son los valores de las variables de bloques o extrañas, y las casillas los niveles de la variable de tratamiento (variable A). Si el experimento se resolviera con un diseño de doble bloqueo; es decir, con tres dimensiones a tres niveles, se tendría un total de 3 x 3 x 3 = 27 casillas. Con el formato de Cuadrado Latino, sólo se realiza un 1/d parte del total; es decir, 1/3(27) = 9 casillas. Se tiene, por lo tanto, un formato más económico para probar el efecto de las distintas dimensiones o variables.

Propiedades básicas Con respecto al diseño de Cuadrado Latino, hay que tener en cuenta dos aspectos básicos: a) en primer lugar, como se ha indicado, cada nivel o valor de la variable de tratamiento (variable A), debe aparecer una y sólo una vez en cada fila y columna; b) en segundo lugar, la colocación de las letras dentro de las casillas puede tomar varias formas asumiendo, como es obvio, la condición anterior. . . //. .

Cada disposición de Cuadrado Latino, 3 x 3, 4 x 4, 5 x 5, etc, tiene una o más formas estándar o prototípicas. Según la forma estándar del Cuadrado Latino, las letras de la primera fila y la primera columna siguen el orden natural (el Cuadrado Latino 3 x 3 representado en la tabla es estándar). El Cuadrado Latino 3 x 3 tiene una forma estándar, pero a medida el orden del cuadrado es mayor se tiene más de un formato estándar. A partir de las formas estándar, mediante intercambio de filas y columnas, se obtienen las formas derivadas. . . //. .

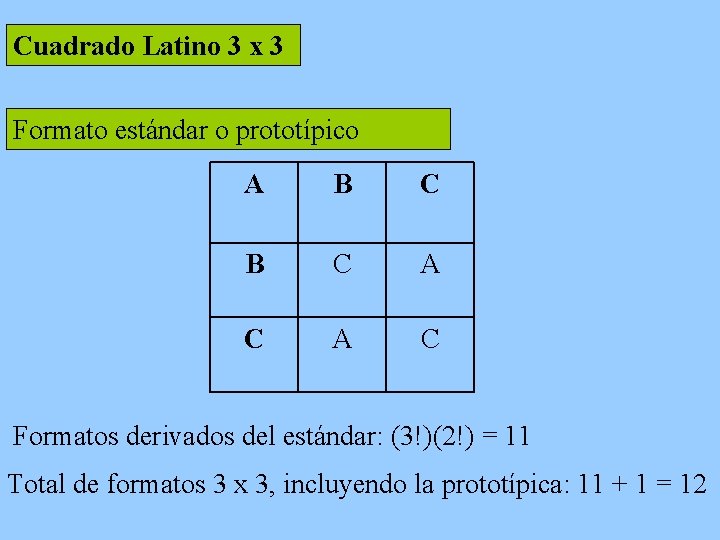
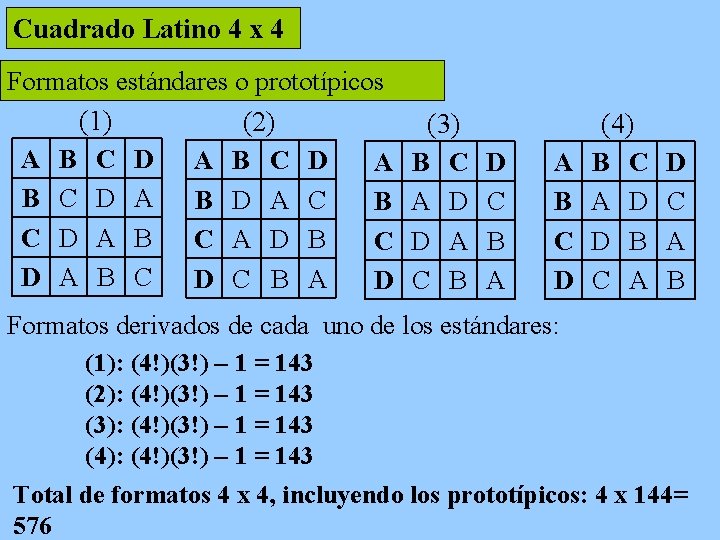
Así, el formato cuadrado 3 x 3 tiene una forma estándar, y (3!)(2!) - 1 = 11 formas derivadas. El total de Cuadrados Latinos de orden 3 x 3 son 12 (una estándar y 11 derivadas). El formato cuadrado 4 x 4 tiene cuatro formas estándar, cada una de las cuales genera (4!)(3!) - 1 = 143 forma derivadas. El total de disposiciones cuadradas 4 x 4 es de 4(144) = 576 Cuadrados Latinos. A medida que se aumenta el tamaño de la dimensión, se dispara la cantidad de posibles formatos. Las principales formas estándar de los Cuadrados Latinos se encuentran en tablas publicadas Fisher y Yates (1953), y Cochran y Cox (1957).

Cuadrado Latino 3 x 3 Formato estándar o prototípico A B C A C Formatos derivados del estándar: (3!)(2!) = 11 Total de formatos 3 x 3, incluyendo la prototípica: 11 + 1 = 12

Cuadrado Latino 4 x 4 Formatos estándares o prototípicos (1) (2) A B C D A B D A C B C D A B C A D B C D A B C D C B A D (3) B C A D D A C B D C B A A B C D (4) B C A D D B C A D C A B Formatos derivados de cada uno de los estándares: (1): (4!)(3!) – 1 = 143 (2): (4!)(3!) – 1 = 143 (3): (4!)(3!) – 1 = 143 (4): (4!)(3!) – 1 = 143 Total de formatos 4 x 4, incluyendo los prototípicos: 4 x 144= 576

Ejemplo práctico Supóngase, por ejemplo, que un investigador estudia el efecto de la longitud de lista sobre la memoria de recuerdo, con la técnica de pares asociados; es decir, con listas de palabras asociadas al número uno o dos. Estas listas varían en longitud, de modo que la primera lista tiene cuatro palabras (condición A 1), la segunda seis palabras (condición A 2), y la tercera ocho palabras (condición A 3). Se trata de contabilizar la cantidad lecturas requeridas por el sujeto para conseguir asociar correctamente los dígitos a las palabras correspondientes. . . //. .

Según este procedimiento, cada sujeto realiza una lectura de la lista de pares asociados o lista de recuerdo y a continuación recibe la misma lista o lista de prueba sin dígitos. La tarea del sujeto consiste en asociar el dígito uno o el dos a las palabras de la lista. Se prosiguen las lecturas y las pruebas hasta que el sujeto logra asociar correctamente todos los dígitos.

Experimento en Cuadrado Latino Dadas las especiales características del experimento, el investigador considera oportuno controlar dos potenciales variables extrañas, para extraer su efecto del error experimental. Estas variables son nivel de ansiedad del sujeto (variable B), y fatiga física o momento del día en que ejecuta el experimento (variable C). Se pretende, mediante la aplicación del diseño de Cuadrado Latino, controlar esas dos fuentes extrañas por su implicación en la variable de respuesta. Asimismo, debido a la dificultad de encontrar sujetos con características ansiógenas similares, se ha desestimado resolver el problema mediante la técnica de doble bloqueo completo. . . //. .

El formato de Cuadrado Latino requiere la selección de tres niveles de variable B, ansiedad baja (B 1), ansiedad media (B 2) y ansiedad alta (B 3), y tres niveles de la variable fatiga física, mañana (C 1), tarde (C 2) y noche (C 3). Puesto que se trata de un diseño con un sujeto por casilla y con formato cuadrado 3 x 3, hay un total de d² = 9 sujetos (siendo d la cantidad de valores por dimensión).

Modelo de prueba estadística Paso 1. Se especifican las hipótesis de nulidad. La hipótesis principal recoge el efecto de los tratamientos, y las hipótesis secundarias los efectos de filas y columnas. Hipótesis principal H 0: 1 = 2 = 3 = 0 Hipótesis secundarias H 0: ß 1 = ß 2 = ß 3 = 0 H 0: 1 = 2 = 3 = 0

Paso 2. La primera hipótesis alternativa está asociada a la hipótesis experimental o hipótesis sobre los tratamientos, y las dos hipótesis alternativas están asociadas a los efectos de filas y columnas, respectivamente. Estas tres hipótesis alternativas tienen la misma expresión. H 1: por lo menos una desigualdad

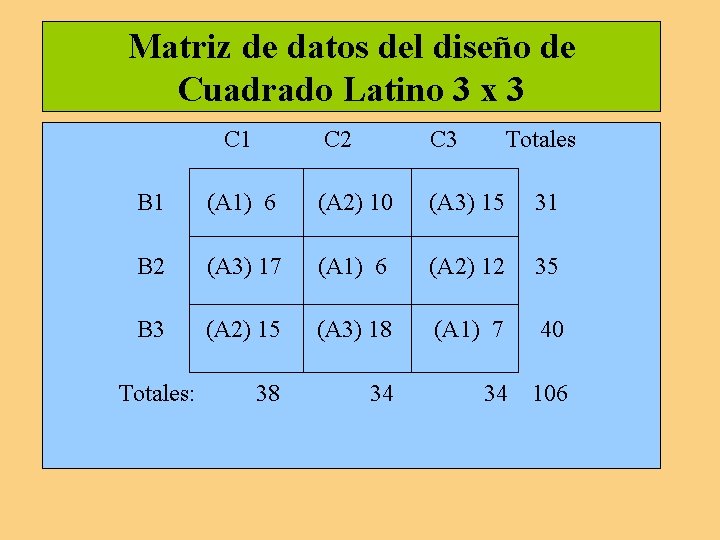
Paso 3. La prueba estadística se basa en el Análisis de la Variancia (F de Snedecor), asumiendo el modelo aditivo y un nivel de significación de 0. 05. Paso 4. Terminado el experimento, se obtiene la correspondiente matriz de datos. De estos datos, se estiman las variancias para el cálculo del valor empírico de F.

Matriz de datos del diseño de Cuadrado Latino 3 x 3 C 1 C 2 C 3 Totales B 1 (A 1) 6 (A 2) 10 (A 3) 15 31 B 2 (A 3) 17 (A 1) 6 (A 2) 12 35 B 3 (A 2) 15 (A 3) 18 (A 1) 7 40 Totales: 38 34 106

Modelo anova El modelo aditivo del diseño Cuadrado Latino es: Yijk = µ + i + ßj + k + ijk donde Yijk es cualquier dato de la matriz, µ constante o media global del experimento, i el efecto del i tratamiento, ßj el efecto de la j fila, k el efecto de la k columna, y ijk el error experimental o de muestreo. Se asume que el error tiene una distribución independiente y normal con media cero y variancia constante (s²). La aplicación correcta del modelo requiere, también, asumir la no presencia de interacciones entre i y ßj, i y k, y entre ßj y k; es decir, se asume que ( ß)ij = 0, ( )ik = 0, y (ß )jk = 0.

Cálculo de las Sumas de Cuadrados Según el modelo estructural propuesto, la Suma de Cuadrados total se divide en: Suma de Cuadrados de tratamientos, Suma de Cuadrados de filas, Suma de Cuadrados de columnas, y Suma de Cuadrados del error. SCtotal = SCtrat. + SCfilas + SCcolum. + SCerror SCtotal = (6)² + (17)² +. . . + (7)² - (106)²/9 = 179. 56 . . //. .

El cálculo de las Sumas de Cuadrados de tratamientos (Variable A) requiere, como paso previo, la agrupación de los distintos valores de la matriz por cada tratamiento. Tratamiento A 1 = 6 + 7 = 19 Tratamiento A 2 = 10 + 12 + 15 = 37 Tratamiento A 3 = 15 + 17 + 18 = 50. . //. .

De esos totales se deriva la variación de los tratamiento. SCtrat. = [(19)²/3 + (37)²/3 + (50)²/3] - (106)²/9 = 161. 55 SCfilas = [(31)²/3 + (35)²/3 + (40)²/3] - (106)²/9 = 13. 55 SCcolum. = [(38)²/3 + (34)²/3] - (106)²/9 = 3. 55 SCerror = SCtotal - SCtrat. - SCfilas - SCcolum. = 0. 91

Resultado del anova Cuadro resumen del ANOVA: diseño Cuadrado Latino 3 x 3 F. V. SC g. l. CM F p Tratamientos(A) 161. 55 (d -1) = 2 80. 77 179. 49 < 0. 01 Filas(B) 13. 55 (d -1) = 2 6. 77 15. 04 > 0. 05 Columnas(C) 3. 55 (d -1) = 2 1. 77 3. 93 > 0. 05 Error(residual) 0. 91 (d -1)(d -2) = 2 0. 45 Total 179. 56 d²- 1 = 8 F 0. 95(2/2) = 19; F 0. 95(2/2) = 99

Modelo de prueba estadística Paso 5. De los resultados del análisis se infiere que el efecto de los tratamientos es muy significativo, con probabilidad de error del uno por ciento. En cuanto a las variables extrañas, tanto el efecto de filas como el de columnas no son significativos al 5% y se aceptan las hipótesis de nulidad.

Diseños jerárquico o anidado

Diseño anidado o jerárquico El diseño anidado, conocido también por diseño jerárquico, es un formato de investigación frecuentemente utilizado en ámbitos educativos, sociales y clínicos aplicados. Inicialmente, recibió el nombre de diseño de grupos intra-tratamientos, dado que los grupos se anidan dentro de los distintos valores de la variable de tratamiento. Así, los distintos grupos son asignados a los niveles de la variable independiente, no dándose una relación de combinación entre la variable de grupos y la variable de tratamiento. . . //. .

En otras palabras, los valores de la variable de grupos no se repiten para los valores de la variable de tratamiento. Definida la estructura de anidación de los grupos intra tratamientos, de cada grupo se eligen al azar los sujetos experimentales

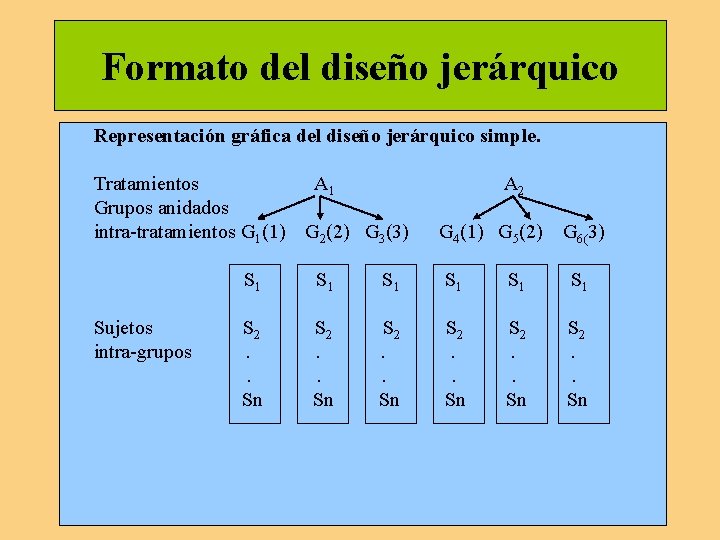
Formato del diseño jerárquico Representación gráfica del diseño jerárquico simple. Tratamientos A 1 A 2 Grupos anidados intra-tratamientos G 1(1) G 2(2) G 3(3) G 4(1) G 5(2) G 6(3) S 1 S 1 Sujetos S 2 S 2 intra-grupos . . Sn Sn

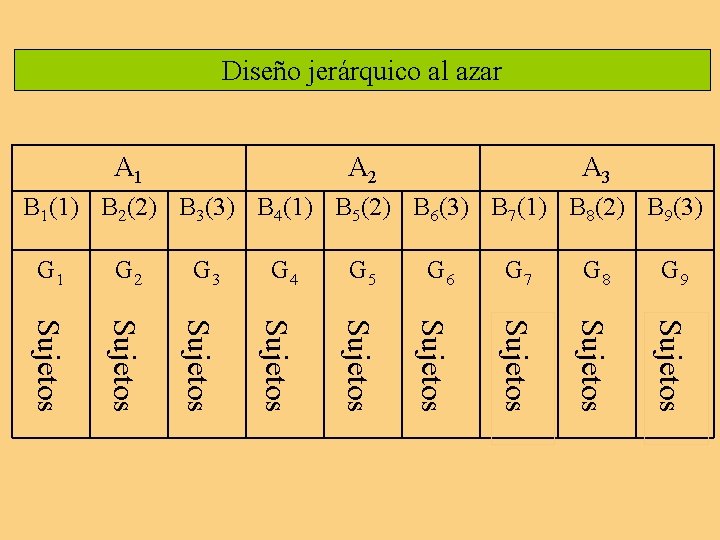
Diseño jerárquico al azar A 1 A 2 A 3 B 1(1) B 2(2) B 3(3) B 4(1) B 5(2) B 6(3) B 7(1) B 8(2) B 9(3) G 1 G 2 G 3 G 4 G 5 G 6 G 7 G 8 G 9 Sujetos Sujetos Sujetos

Ventajas Desde el punto de vista práctico, esta estructura de diseño permite estimar el efecto de los grupos; es decir, el posible efecto social o institucional que el grupo ejerce sobre el individuo. La pertenencia a un grupo determinado (aula, centro, barrio, etc. ) es capaz determinar, en muchos casos, la actuación de los individuos. De ahí, la ventaja de los diseños jerárquicos ya que se introduce en el modelo ese posible efecto y, por esa razón, se controla.

Fuentes de variación del diseño 1. La variación de los tratamientos o niveles de la variable independiente (A). 2. La variación de los grupos o variable anidada (B). Téngase en cuenta que la especial composición del grupo puede afectar a la variabilidad de las unidades y los datos. 3. Por último, la variación de las diferencias individuales es una fuente residual y determina la variación del error.

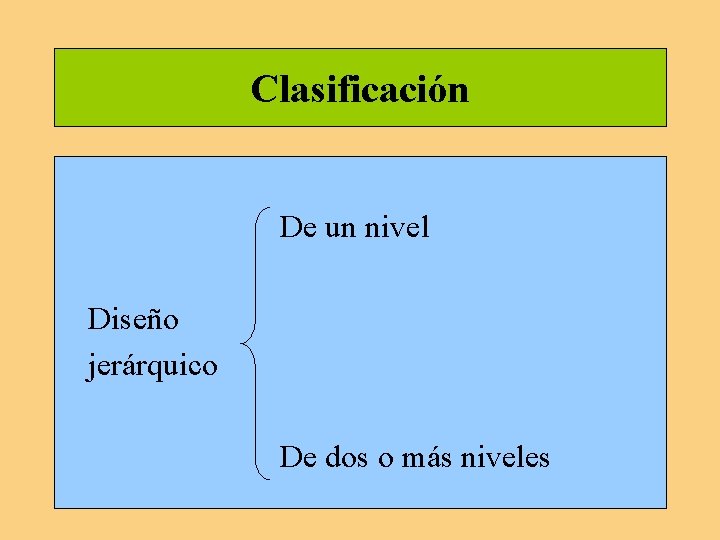
Clasificación De un nivel Diseño jerárquico De dos o más niveles

Caso paramétrico. Ejemplo Se pretende estudiar la eficacia de tres métodos distintos de comprensión verbal, en escolares de primer nivel de enseñanza básica. A tal propósito, se eligen los tres métodos siguientes: método tradicional (A 1), audio-visual (A 2) y economía de fichas (A 3). Para ejecutar el experimento, se obtienen muestras aleatorias de n = 6 sujetos de seis escuelas diferentes con idéntico nivel escolar. . . //. .

Al mismo tiempo, se pretende controlar el posible efecto institucional de la escuela sobre los individuos. Finalizada la experiencia, se aplica a los escolares una prueba de comprensión verbal de 40 ítems.

Modelo de prueba estadística Paso 1. En términos de efectos de la variable de tratamiento, se asume su nulidad. Es decir, asume que los tres efectos son cero: H 0: 1 = 2 = 3 = 0 La hipótesis secundaria relativa al factor anidado se expresa por: H 0: ß 1 = ß 2 = ß 3 = ß 4 = ß 5 = ß 6 = 0

Paso 2. La hipótesis alternativa, asociada a la hipótesis experimental, especifica que hay al menos una diferencia o desigualdad entre los tres niveles de tratamiento. H 1: por lo menos una desigualdad Esta hipótesis es común tanto para la variable de tratamientos como para la variable de grupos.

Paso 3. La prueba estadística es el Análisis de la Variancia (estadístico F), con modelo aditivo y nivel de significación de = 0. 05. Paso 4. De la ejecución del experimento, se obtienen la correspondiente la matriz de datos. Con estos datos se estiman las variancias y se computan los valores empíricos de las F correspondientes a las hipótesis nulas planteadas.

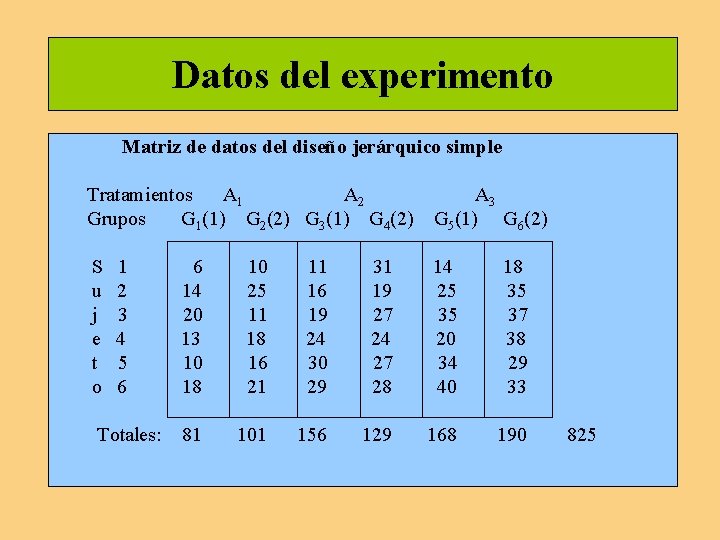
Datos del experimento Matriz de datos del diseño jerárquico simple Tratamientos A 1 A 2 A 3 Grupos G 1(1) G 2(2) G 3(1) G 4(2) G 5(1) G 6(2) S 1 6 10 11 31 14 18 u 2 14 25 16 19 25 35 j 3 20 11 19 27 35 37 e 4 13 18 24 20 38 t 5 10 16 30 27 34 29 o 6 18 21 29 28 40 33 Totales: 81 101 156 129 168 190 825

Modelo ANOVA del diseño Yijk = µ + j + ßk/j + ij

Yijk = cualquier observación o dato del experimento. µ = la constante o media total del experimento. j = el efecto de un determinado nivel jota de la variable de tratamiento. ßk/j = el efecto del k nivel del factor de grupos o factor anidado de carácter aleatorio y se asume que tiene una distribución normal e independiente con media cero y variancia constante (s²ß). ijk = la variable aleatoria de error que se asume es independiente y normalmente distribuida con media cero y variancia constante (s²).

Descomposición de las Sumas de Cuadrados del ANOVA SCtotal = SCgrupos + SCintra-grupos Según esa primera descomposición, la variable de grupos está formada por ab grupos (siendo a la cantidad de tratamientos, y b la cantidad de grupos por tratamiento). Nótese que la variación total se divide en dos grandes fuentes, la variación entre grupos (B) y la variación intra-grupos. A su vez, la variabilidad asociada a los grupos se divide en: variabilidad entre los tratamientos (A) y variabilidad de los grupos intra niveles de A. . . //. .

Sumas de Cuadrados del ANOVA SCgrupos = SCA + SCB/A Así, se consigue la estructura definitiva del diseño: SCtotal = SCA + SCB/A + SCS/B/A

Cálculo de las Sumas de cuadrados SCtotal = (6)² + (14)²+. . . + (33)² - (825)²/36 = 2877. 75 SCgrupos = [(81)²/6 + (101)²/6 +. . . + (190)²/6] – (825)²/36 = 1437. 58 SCerror = (6)² + (14)² +. . . + (33)² - [(81)²/6 + (101)²/6 +. . . + (190)²/6] = 1440. 17

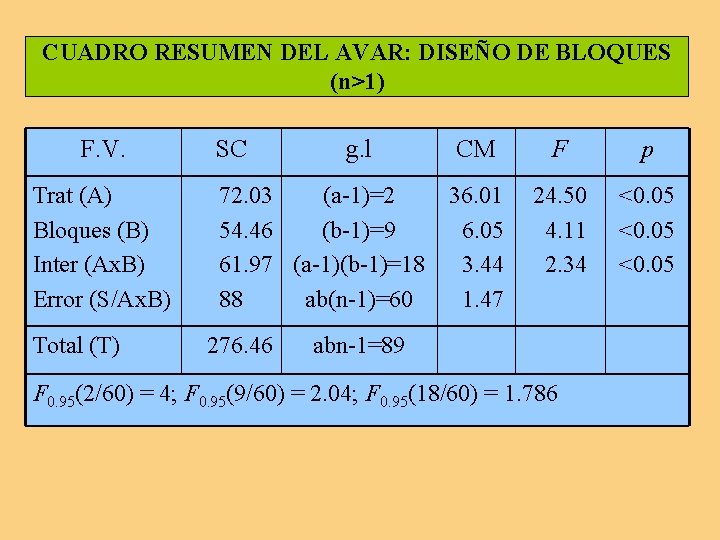
Cálculo de las Sumas de cuadrados SCtrat. = [(81+101)²/12 +. . . + (168+190)²/12] - (825)²/36 = 1303. 17 SCgrupos/trat. = SCgrupos - SCtrat. = [(81)² + (191)² +. . . + (190)²]/6 - [(81+101)²/12 + (129+156)²/12 + (168+190)²/12] = 134. 41

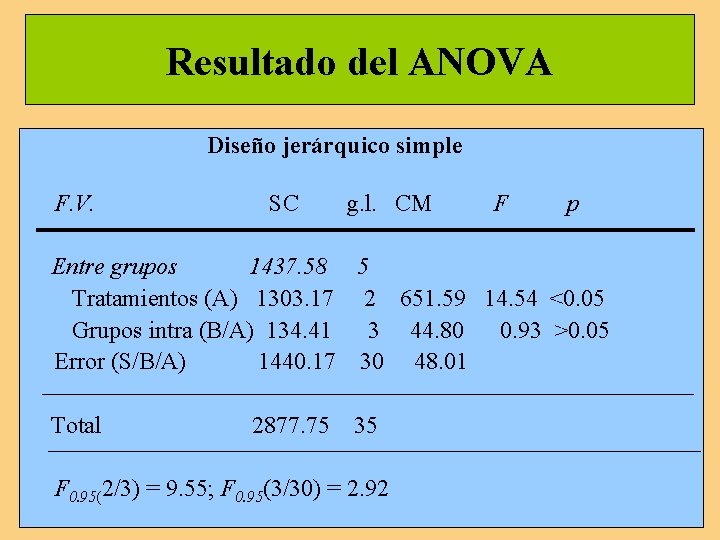
Resultado del ANOVA Diseño jerárquico simple F. V. SC g. l. CM F p Entre grupos 1437. 58 5 Tratamientos (A) 1303. 17 2 651. 59 14. 54 <0. 05 Grupos intra (B/A) 134. 41 3 44. 80 0. 93 >0. 05 Error (S/B/A) 1440. 17 30 48. 01 Total 2877. 75 35 F 0. 95(2/3) = 9. 55; F 0. 95(3/30) = 2. 92

Hipótesis de nulidad del diseño Términos de contraste o denominadores de las razones F de las pruebas de las hipótesis de nulidad del experimento F. V. F F 0. 95 Entre tratamientos CMA/CMB/A = 14. 54 9. 55 Entre grup. intra A CMB/A/CMS/B/A = 0. 93 2. 92

Modelo de prueba estadística Paso 5. Del resultado del análisis de del diseño anidado o jerárquico de un solo factor, se concluye la no-aceptación de la hipótesis de nulidad para la variable de tratamiento y sí, en cambio, para la variable de grupos.

Fin del tema VI