TEMA N 1 Conjuntos numricos Aprendizajes esperados Utilizar

TEMA Nº 1 Conjuntos numéricos

Aprendizajes esperados: • Utilizar y clasificar los distintos conjuntos numéricos en sus diversas formas de expresión, tanto en las ciencias exactas como en las ciencias sociales y en el ámbito cotidiano. • Percibir la matemática como una disciplina en evolución y desarrollo permanente. • Aplicar la operatoria básica en los números naturales y enteros.

• Aplicar las operaciones básicas y propiedades de los números racionales. • Resolver problemas que involucren operaciones con números enteros, decimales y fracciones. • Reconocer regularidades numéricas (secuencias).

Conjuntos Numéricos 1. Números Naturales 1. 1 Consecutividad numérica 1. 2 Paridad e imparidad 1. 3 Números primos 1. 4 Múltiplos y divisores 1. 5 Mínimo Común Múltiplo y Máximo Común Divisor 1. 6 Operatoria en los naturales 2. Números Cardinales 3. Números Enteros 3. 1 Operatoria en los enteros 3. 2 Propiedades 3. 3 Prioridad de las operaciones

4. Números racionales (Q) 4. 1 Propiedades de los racionales 4. 2 Operatoria en los racionales 4. 3 Transformaciones de números racionales 4. 4 Comparación de fracciones 4. 5 Secuencia numérica 5. Números irracionales (Q*) 6. Números reales ( IR ) 7. Números imaginarios ( II ) 8. Números complejos ( C )

1. Números Naturales (N) Conjunto de la forma: IN = {1, 2, 3, 4, 5, …}, conjunto infinito. 1. 1 Consecutividad numérica • Sucesor Todo número natural tiene un sucesor, y se obtiene sumando 1 al número, es decir: Si n pertenece a IN, su sucesor será n + 1.

• Antecesor: Todo número natural (exceptuando el 1), tiene un antecesor, y se obtiene al restar 1 al número, es decir: Si n pertenece a IN, su antecesor será n - 1 Naturales Consecutivos n-1 antecesor n n+1 sucesor

1. 2 Paridad e imparidad • Números Pares {2, 4, 6, 8, 10……, 2 n} Son de la forma 2 n, con n en los naturales. Sucesor par: Se obtiene sumando 2 al número. Si el número es 2 n, entonces su sucesor es 2 n+2. Antecesor par: Se obtiene restando 2 al número. Si el número es 2 n, entonces su antecesor es 2 n-2. 2 n - 2 Antecesor par 2 n 2 n + 2 Sucesor par

• Números Impares {1, 3, 5, 7, 9…… , 2 n-1} Son de la forma 2 n-1, con n en los naturales. Sucesor impar: Se obtiene sumando 2 al número. Si el número es 2 n-1, entonces su sucesor es 2 n+1. Antecesor impar: Se obtiene restando 2 al número. Si el número es 2 n-1, entonces su antecesor es 2 n-3. 2 n - 3 2 n -1 Antecesor impar 2 n + 1 Sucesor impar

o pl os l t Se i p l al lla os y m m a u Po l tip “m r l ica últ ej e i p r m l d ic o ” 1. 3 Números Primos • ú M lt ú ipl Son aquellos números que son sólo divisibles por 1 y por sí mismos: { 2, 3, 5, 7, 11, 13, 17, 19, 23, 29…} . 4 1 Nota: El 1 no es primo. M Di

• Divisores Se llama “divisor” de un número, aquel valor que lo divide exactamente. (Está contenido en él, una cantidad exacta de veces) Por ejemplo: Los divisores de 24 son los números que lo dividen exactamente: {1, 2, 3, 4, 6, 8, 12 y 24} Nota: El 5 no es divisor de 24, ya que al dividir 24 por 5 resulta 4, 8.

• Mínimo Común Múltiplo El mínimo común múltiplo (m. c. m. ) de dos o más números, corresponde al menor de los múltiplos que tienen en común. Ejemplo: -Algunos múltiplos de 3 son: {3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, …, 60} -Algunos múltiplos de 6 son: {6, 12, 18, 24, 30, 36, 42, 48…, 60} -Algunos múltiplos de 15 son: {15, 30, 45, 60, 75, …}

El m. c. m. entre 3, 6 y 15 es 30. (Dentro de los múltiplos que tienen en común, 30 es el menor). El m. c. m. entre 3, 6 y 15 se puede obtener a través del siguiente método: Se divide por números primos hasta que en cada columna quede 1, y el producto de ellos corresponde al m. c. m. 3 6 15 3 1 2 5 2 2 1 3 5 1 m. c. m. = 3 ∙ 2 ∙ 5 =30 5

• Máximo Común Divisor El máximo común divisor (M. C. D. ) de dos o más números, corresponde al mayor número que los divide simultáneamente. Ejemplo: -Los divisores de 36 son: {1, 2, 3, 4, 6, 9, 12, 18, 36} -Los divisores de 18 son: {1, 2, 3, 6, 9, 18} -Los divisores de 24 son: {1, 2, 3, 4, 6, 8, 12, 24}

El M. C. D. entre 36, 18 y 24 es 6. (Dentro de los divisores que tienen en común, 6 es el mayor). El M. C. D. entre 36, 18 y 24 se puede obtener a través del siguiente método: Se divide por números primos que sean divisores de cada número, hasta que ya no se pueda dividir a todos en forma simultánea. 36 18 24 2 18 9 12 3 6 3 4 M. C. D. = 2 ∙ 3 = 6

1. 6 Operaciones en IN • Adición, sustracción, multiplicación y división Esta información se encuentra en tu libro en la página 18. Propiedades de la Adición: a) Clausura: La suma de dos números naturales es siempre un natural. b)Conmutativa: Si a y b son números naturales, entonces se cumple que: a+b=b+a Por ejemplo: 12 + 5 = 5 + 12

c) Asociativa: Si a, b y c son números naturales, entonces se cumple que: a: r a + (b+c) = (a+b) + c Ejemplo: 13 + (5+9) = (13+5) + 9 13 + (14) =(18) + 9 27 = 27 us u a a ) Cl Nota: En los naturales no existe neutro aditivo. s a d e p i ed o Pr a E l M e pr u s l t s odu i i e m c pr to d e un e de l

b)Conmutativa: Si a y b son números naturales, entonces se cumple que: Por ejemplo: c) Asociativa: 34∙ 5 = 5∙ 34 Si a, b y c son números naturales, entonces se cumple que: a (b∙c) = (a∙b) c Por ejemplo: 4 ∙ (5∙ 3) = (4∙ 5) ∙ 3 4 ∙ (15) = (20) ∙ 3 Nota: El elemento neutro de la multiplicación es el 1. ás rm Ve en la s pá g ina s 18 y 1 9 de l L i b ro.

2. Números Cardinales ( N 0) Conjunto de la forma: IN 0 = {0, 1, 2, 3, 4, 5, …}, conjunto infinito. 2. 1 Operaciones en IN 0 • Adición, sustracción, multiplicación y división En este conjunto se cumplen las mismas propiedades que en los naturales. La diferencia es que incluye al cero, y por tal razón posee “elemento neutro aditivo”. Si a es un número cardinal, entonces: a+0=0+a=a

3. Números Enteros (Z) Conjunto de la forma: Z = {…, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, …}, infinito. Se puede representar como: Z = Z- U IN 0 Z = Z- U {0} U Z+ Recta numérica: -3 -2 -1 0 1 2 3 Z- Z+

Valor absoluto: El valor absoluto de un número representa la distancia del punto al origen (cero de la recta numérica). Por ejemplo, la distancia del 5 al origen es cinco unidades, igual que la distancia del -5 al origen. La notación es: |5| = 5 y |-5| = 5 -5 Luego, 5 unidades |-20| = 20 0 5 unidades |34| = 34 5 |-12| = 12…

3. 1 Operaciones en Z Al realizar sumas, restas, multiplicaciones y divisiones en los enteros, debemos considerar algunas reglas con respecto a los signos: Si a y b son números entonces, se cumple que: a) a + -b = a – b Ejemplo: 5 + - 9 = 5 – 9 = -4 b) a – (-b) = a + b Ejemplo: 12 – (-8) = 12 + 8 = 20

c) Al sumar enteros de igual signo, éste se mantiene. Ejemplo: 25 + 8 = +33 -5 + - 9 = -14 d) Al sumar enteros de distinto signo, se calcula la diferencia entre sus valores absolutos, conservando el signo del mayor. Ejemplo: -10 + 7 = -3 75 + -9 = +66

e) Si a y b son dos números enteros de igual signo (positivos o negativos), entonces: - El producto y el cuociente entre ellos es positivo. Ejemplo: -42 ∙ -8 = + 336 28 : 7 = + 4 f) Si a y b son dos números enteros de distinto signo, entonces: - El producto y el cuociente entre ellos es negativo. Ejemplo: 37 ∙ -5 = -185 125 : -5 = -25

3. 2 Propiedades La suma de números enteros cumple con la propiedad Conmutativa y Asociativa. Ejemplo: (-3) + 2 = 2 + (-3) -1 = -1 La suma en los números enteros tiene “elemento neutro”: el cero. Ejemplo: (-8)+ 0 = -8

3. 3 Prioridad en las operaciones Tanto en los números naturales como en los enteros, hay operaciones que tienen prioridad sobre otras. Existe un orden para resolver ejercicios como: -5 + 15 : 3 - 3 = ? ¿Qué se resuelve primero? El orden para ejecutar las operaciones que involucran paréntesis y operaciones combinadas es: 1° Paréntesis 2° Potencias 3° Multiplicación y/o división (de izquierda a derecha) 4° Adiciones y sustracciones

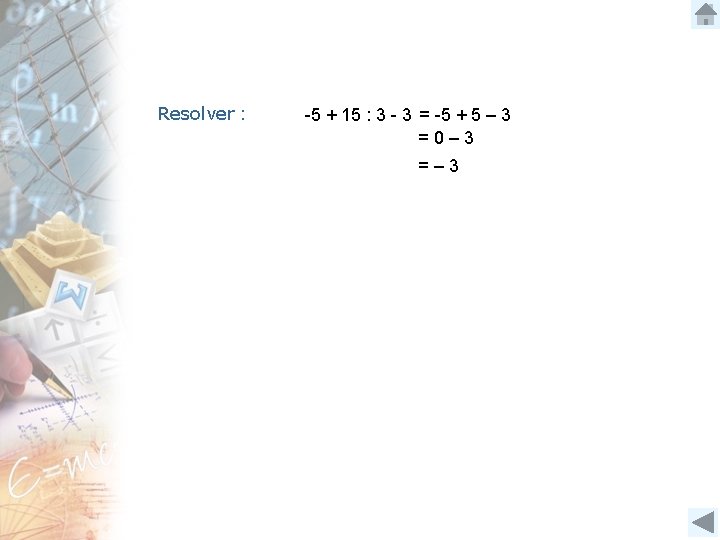
Resolver : -5 + 15 : 3 - 3 = -5 + 5 – 3 =0– 3 =– 3

4. Números Racionales (Q) Es el conjunto de todos aquellos números que se pueden escribir como fracción, es decir: Q= a b / a y b son enteros, y b es distinto de cero a: numerador y b: denominador Ejemplos: 2; 17; 0; -6; -45; -1; 14; -2; 0, 489; 2, 18; -0, 647 8 3 7 15, 0 NO es racional

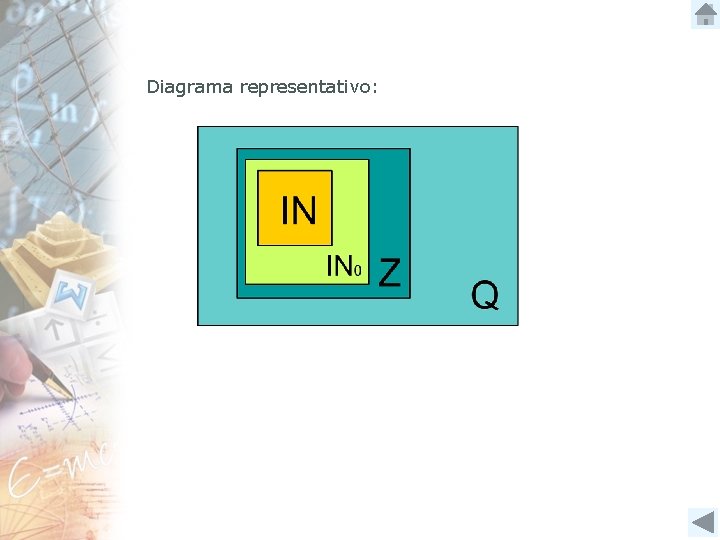
Todo número entero es racional. Por ejemplo: 3 es Natural (3 3 es Cardinal (3 3= 3 1 IN IN), IN 0), y como , 3 es racional IN 0 Z Q (3 Q).

Diagrama representativo:

4. 1 Propiedades de los racionales (pág. 23 del libro) • Amplificar y simplificar fracciones Amplificar una fracción, significa multiplicar, tanto el numerador como denominador por un mismo número. Ejemplo: Al amplificar la fracción 2 3 2∙ 6 3∙ 6 = 12 18 por 6 resulta:

Simplificar una fracción, significa dividir, tanto el numerador como denominador por un mismo número. Ejemplo: Al simplificar la fracción 27 45 27 : 3 45 : 3 = por 3 resulta: 9 15 • Inverso multiplicativo o recíproco de una fracción Ejemplo: El inverso multiplicativo, o recíproco de 2 9 es: 9 2

4. 2 Operatoria en los racionales (pág. 24 del libro) • Suma y resta Ejemplos: 1. Si los denominadores son iguales: 4 15 + 7 15 = 11 y 15 4 15 - 7 15 = -3 15 2. Si uno de los denominadores es múltiplo del otro: 2 15 + 7 45 = 2∙ 3 + 7∙ 1 45 = 6+7 45 = 13 45

3. Si los denominadores son primos entre sí: 4 5 + 7 8 = 4∙ 8 + 5∙ 7 40 = 32 + 35 40 67 = 40 4. Aplicando mínimo común múltiplo (m. c. m. ): 5 12 + 7 18 = 5∙ 3 + 7∙ 2 36 = 15 + 14 36 = 29 36

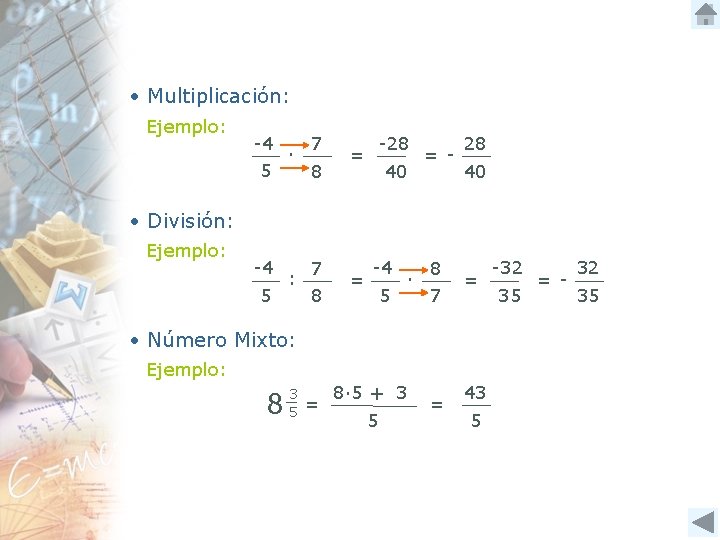
• Multiplicación: Ejemplo: -4 5 ∙ 7 8 -28 = 40 = - 28 40 • División: Ejemplo: -4 5 : 7 8 = -4 5 ∙ 8 7 = • Número Mixto: Ejemplo: 8 3 5 = 8∙ 5 + 3 5 = 43 5 -32 35 = - 32 35

4. 3 Transformación de números racionales (pág. 24 del libro) • De fracción a decimal: Se divide numerador por denominador. Ejemplo: 7 = 1, 75 4 • De decimal finito a fracción: El numerador corresponde al número sin coma, y el denominador es una potencia de 10 que depende del número de decimales que tenga el número. Ejemplo: 1, 75 = 175 = 25∙ 7 = 7 100 4 25∙ 4

• De un número decimal periódico a fracción: 1. El numerador de la fracción es la diferencia entre el número decimal completo, sin la coma, y la parte entera. 2. El denominador está formado por tantos nueves (9), como cifras tenga el período. Ejemplo 1: 2, 35 = 235 – 2 = 233 99 99 Ejemplo 2: 0, 376 = 376 – 0 = 376 999

• De un número decimal semi periódico a fracción: 1. El numerador de la fracción corresponde a la diferencia entre el número decimal completo, sin la coma; y la parte entera incluyendo las cifras del ante período. 2. El denominador queda formado por tantos nueves (9), como cifras tenga el período, y seguido de tantos ceros (0), como cifras tenga el ante período. Ejemplo: 3, 21 = 321 -32 = 90 289 90 Nota: Se llama “ante período” a los números que hay entre la coma, y el período.

4. 4 Comparación de fracciones (pág. 25 del libro) • Multiplicación cruzada: Ejemplo: Al comparar 13 15 y 9 (Multiplicando cruzado) 10 13 ∙ 10 y 15 ∙ 9 130 y 135 Como 130 < 135, entonces: 13 15 < 9 10

• Igualar denominadores: Ejemplo: Al comparar 13 15 13∙ 4 15∙ 4 52 60 Como 52 > 35, y y y 7 (Igualando denominadores) 12 7∙ 5 12∙ 5 35 60 entonces 13 15 > 7 12

• Transformar a decimal: Ejemplo: Al comparar 13 y 7 15 12 13 15 7 12 (Transformando a decimal) = 0, 86666666… = 0, 58333333… Como 0, 86 > 0, 583 , entonces 13 > 7 15 12

4. 5 Secuencia Numérica Ejemplo: En la secuencia: 6 5 , 16 , 5 26 , 36 , . . . 5 5 ¿Qué número tendríamos que sumar a para obtener el 7° término ? 1 , 5 Respuesta: De acuerdo a las características de la secuencia, el 7° término es 66. 5 Tendríamos que sumar 65 obtener el 7° término. 5 Es decir: 65 = 13 5 a 1 5 , para

Observación: La secuencia anterior también se puede analizar de la siguiente manera: 1 +1, 5 1 +3, 5 1° 2° 1 +5, 5 3° 1 + 7 , . . . , 1 + 13… 5 5 4° . . . , 7°… Lo que nos permitiría saber, por ejemplo, ¿cuál es el valor del n-ésimo término de la secuencia? Respuesta: Es 1 , más un número impar, lo que se expresa como: 5 1 + (2 n - 1) 5 (Con n = posición del término)

5. Números Irracionales (Q*) Son aquellos que NO se pueden escribir como una fracción (decimales infinitos NO periódicos). Q* = U Q Q*=

6. Números Reales (IR) Es el conjunto formado por la unión entre los números racionales y los números irracionales. IR = Q U Q* Ejemplos: 3, -89, -2; 2, 18; 7 Diagrama representativo: 23, 491002

7. Números imaginarios (II) Todos aquellos números que NO son reales, son imaginarios. U IR II = O Ejemplo: Raíces de índice par y parte subradical negativa:

8. Números complejos (C) Es el conjunto formado por la unión entre los números reales y los números imaginarios. Ejemplos: 5, -68, -1; 8 Diagrama representativo: -0, 647

Los contenidos revisados anteriormente los puedes encontrar en tu libro, desde la página 14 a la 28.