Tema 5 El lenguaje de la lgica de













































- Slides: 45

Tema 5. El lenguaje de la lógica de primer orden b. Formalización del lenguaje natural

Sentencias • No todas las fórmulas expresan oraciones. Sea el predicado P ser pequeño. Compárense: Pa Px x. Py Sólo Pa y x. Px expresan oraciones, i. e. , enunciados con valor de verdad: Pa afirma que Frodo es pequeño x. Px afirma que todo el mundo es pequeño Para tener valor de verdad una expresión debe decir algo acerca de un individuo o de un conjunto de ellos

Sentencias • Fórmulas como Px y x. Py expresan afirmaciones “indeterminadas”: Px viene a decir que x es pequeño • No hay que confundir esta expresión con ‘Alguien es pequeño’. Esta última está cuantificada y se expresa como x. Px x. Py también está cuantificada, pero las variables no “casan” entre sí. La variable x “pegada” al existencial no está dentro del alcance de éste.

Alcance del cuantificador • El ALCANCE de un cuantificador es la fórmula que le sigue inmediatamente: • El alcance de x en las siguientes fórmulas es: x. Px Px x(Px Qx) Px Qx x(Px x. Qx) Px x. Qx Obsérvese la función de los x. Px x. Qx Px paréntesis x y. Rxy y x. Rxy xy x=y

Ejercicio: Alcance del cuantificador • ¿Cuál será el alcance de x en estas fórmulas? x. Px Qx x¬ y. Rxy yxz (y=x z=x) y¬ x¬Qx x. Qa x xyz y(Py x. Qx) x x=a x≠b Px ¬ y. Rxy z (y=x z = x) ¬Qx Qa No es fórmula Qx x =a

Variables libres y ligadas • Una variable está LIGADA ssi ocurre dentro del alcance de un cuantificador que tiene esa variable inmediatamente a su derecha. • Una variable está LIBRE ssi no está ligada x ligada: x libre: x. Px Px Py x. Px x. Py Px yx(Py Rxy) y(Py Rxy) x( y. Py x =a) x y. Py x =a

Variables libres y ligadas • Cada aparición de una variable o término en una fórmula, es una ocurrencia de aquélla. • Una variable puede tener ocurrencias libres y ligadas en una misma fórmula. • Compárense las ocurrencias ligadas y libres en las siguientes fórmulas: y(Rxy x. Rxy) x. Px Qx y( x. Px Rxy) xy z(x=z y=z) x=y

Ejercicio: variables libres y ligadas • ¿Hay alguna variable libre en estas fórmulas? x. Px Qx x¬ y. Rxy yxz (y=x z=x) y¬ x¬Qx x. Rxx x(Qxy y. Qyx) x y( z(Px Rxy) Pz) x( y. Py ( z. Rxz x. Rzx) x x=a x≠b la 2ª x no no no la 1ª y la z no fórmula: falta ) la 2ª x

Sentencia y fórmula libre • Una fórmula es SENTENCIA (i. e. , un enunciado con valor de verdad) ssi no contiene variables libres • Una fórmula con al menos una variable libre es una FÓRMULA ABIERTA Sentencias Fórmulas abiertas Rab Rba Rax Rxa x(Px Qx) x. Px Qx yx(Py Rxy) x x=a y y≠b x y=a y x≠b

Sentencia y fórmula libre • Las sentencias pueden ser enunciados de 2 tipos: - PARTICULARES: sentencias que no contienen ninguna variable - GENERALES: sentencias que contienen alguna variable cuantificada Particulares Generales Pa y Py ¬Qb Pc x¬Qx y. Py Rab Rba xy(Rxy Ryx) a=c c=b x(a=x y x=y)

Ejercicio: sentencia y fórmula libre • ¿Es sentencia? ¿De qué tipo? no es sentencia x. Px ( y. Py Qx) x. Rax x=a x=b no fórmula x( y. Py z. Rxz) xz. Rzx sentencia general x. Qay y. Qxb no es sentencia xy(Qxy y. Qyx) Qab sentencia general x y( z(Pa Rab) Py) sentencia general sentencia particular yxz (a=b b=c) no es sentencia x x=a (x=b x=c)

Formalización del lenguaje natural • Al traducir una oración a L 1 el resultado debe ser siempre una sentencia: nunca pueden quedar en la fórmula variables que no estén ligadas por ningún cuantificador. • Lo primero será, entonces: a) Identificar los individuos o grupos de individuos sobre los que se está predicando algo b) Identificar si la relación que establece lo que se predica de ellos es monaria, binaria, ternaria…

Identificando individuos Si Bilbo es hobbit, vive la Comarca: Barad-Dûr es más alto que la Torre Oscura Mi amigo el orco se ha comido a tu perro ‘Smeagol’ es el nombre hobbit de Gollum El mayor número primo es impar El padre del padre de Gimli era elfo

Identificando grupos de individuos CUANTIFICADOR UNIVERSAL • Las partículas más típicas que lo indican son: Todo es de color de rosa Todo el mundo teme a Sauron Todos los elfos aman la poesía Los elfos aman la poesía Todo aquel que odia a Sauron, ama a Frodo Cualquier enano desprecia a los elfos Quien ama a Frodo, no odia a Sam

Identificando grupos de individuos CUANTIFICADOR EXISTENCIAL • Las partículas más típicas que lo indican son: Alguien no teme a Sauron Hay algo en el bolsillo de Frodo Al menos un hobbit ha salido de la Comarca Algunos elfos no son cursis Unos orcos han secuestrado a Pippin Unos pocos hobbits han salvado a muchos Casi todos los orcos envidian a ciertos hobbits

Identificando grupos de individuos AMBIGÜEDADES El único orco bueno es Gutiérrez (particular) El único orco bueno es el orco muerto (genérico) Quien desea el Anillo, busca a Frodo (todo aquel) Nadie ha visto la cara de quien desea el anillo (el individuo particular que lo desea) La venganza es un plato que se toma frío (genérico) La venganza de Sauron será terrible (particular)

Identificando grupos de individuos NADIE, NINGUNO • Estas expresiones pueden formalizarse tanto con el universal como con el existencial: Nadie es perfecto = i) Dado un individuo cualquiera, no es perfecto x¬Px ii) No es cierto que al menos uno es perfecto ¬ x. Px Esto no supone ambigüedad, puesto que ambas expresiones son equivalentes

Identificando grupos de individuos Los 4 tipos básicos de enunciados Universal afirmativo: TODO P ES Q negativo: NINGÚN P ES Q x(Px Qx) x(Px ¬Qx) ¬ x(Px Qx) Particular x(Px Qx) afirmativo: ALGÚN P ES Q negativo: ALGÚN P NO ES Q x(Px ¬Qx)

Identificando grupos de individuos ¿Por qué ‘Todo P es Q’ se formaliza como un condicional? Compárense: 1. Todos los suizos son europeos 2. Todos los europeos son suizos Detectamos fácilmente una asimetría entre 1 y 2. 1 dice que SI uno es suizo, uno es europeo 2 dice que SI uno es europeo, uno es suizo El condicional nos permite reflejar esta asimetría.

Identificando grupos de individuos En cambio, en ‘Algún P es Q’ no hay tal asimetría: 1. Algunos suizos son banqueros 2. Algunos banqueros son suizos 1 y 2 afirman lo mismo: no puede ser que una sea verdadera y la otra no. Para que sea verdadera, debe ocurrir que haya al menos un individuo que satisfaga a la vez las propiedades de ser suizo y banquero

Identificando grupos de individuos Consideremos ‘Ningún P es Q’: Ningún orco es vegetariano Podemos leerlo de 2 maneras diferentes: i) Dado un individuo cualquiera, si es orco, entonces no es vegetariano: x(Px ¬Qx) ii) No es cierto que haya al menos un individuo tal que es orco y vegetariano: ¬ x(Px Qx) Esto no supone ambigüedad, sino que ambas expresiones son equivalentes

Ejercicios de formalización Si Bilbo es hobbit, vive en la Comarca: Bilbo = a, la Comarca = b Ha ser hobbit = H, vivir en = V Vab Barad-Dûr es más alto que la Torre Oscura B-D = a la T. O. = b ser más alto que = A Aab Mi amigo el orco se ha comido a tu perro mi amigo…= a tu perro = b comer = C Cab

Ejercicios de formalización ‘Smeagol’ es el nombre hobbit de Gollum ‘S’ = a el nombre… = b El mayor número primo es impar el mayor nº…= a ser impar = I a=b Ia El padre del padre de Gimli era elfo el padre de…de G = a ser elfo = E Ea No tenemos aún recursos para expresar la estructura de a

Ejercicios de formalización Todo es de color de rosa ser rosa = R Todo el mundo teme a Sauron S = c temer = T Todos los elfos aman la poesía Los elfos aman la poesía = a ser elfo = E amar = A x Rx x. Txc x(Ex Axa) Nótese que hemos “reificado” la poesía

Ejercicios de formalización Todo aquel que odia a Sauron, ama a Frodo F = a S = c odiar = O amar = A x(Oxc Cualquier enano desprecia a los elfos poesía = a ser enano = N ser elfo = E despreciar = D xy((Nx Axa) Ey) Dxy) Quien ama a Frodo, no odia a Sam F = a Sam = b amar = A odiar = O x(Axa ¬Oxb)

Ejercicios de formalización Alguien no teme a Sauron S = c temer = T Hay algo en el bolsillo de Frodo el b. de F. = a estar en = E x¬Txc x. Exa Al menos un hobbit ha salido de la Comarca la Com = a ser hobb = H salir de = S x(Hx Algunos elfos no son cursis ser elfo = E ser cursi = C Sxa) x(Ex ¬Cx)

Ejercicios de formalización Unos orcos han secuestrado a Pippin = a ser orco = O secuestrar = S x(Ox Sxa) Unos pocos hobbits han salvado a muchos ser hob =H salvar = S xy(Hx Sxy) Casi todos los orcos envidian a ciertos hobbits ser orco = O ser hob = H envidiar = E xy(Ox Hy Exy)

Cuantificación + identidad • Los cuantificadores no permiten recoger todas las sutilezas del lenguaje natural, pero con la ayuda del signo de identidad se pueden captar relaciones más complejas: Hay al menos dos P … Hay como máximo un P… Hay exactamente n P … Sólo Otro

Cuantificación + identidad HAY AL MENOS DOS… • Necesitamos combinar la idea de ‘al menos uno’ con la idea de diferencia: Hay al menos un hobbit: x. Hx Hay al menos dos hobbits: “Hay al menos un hobbit y otro hobbit y uno es diferente del otro” xy(Hx Hy x ≠ y)

Cuantificación + identidad HAY COMO MÁXIMO DOS. . . Hay como máximo un hobbit: • En este caso la idea de “hay al menos uno” no nos sirve, ya que de “como máximo 1” no se sigue “hay 1” “Si un individuo es hobbit y otro individuo es hobbit, el primero es idéntico al segundo” xy((Hx Hy) x = y) Hay como máximo 2 hobbits: xyz((Hx Hy Hz) (x = y x = z y =z)) Las variables introducen 3 “candidatos” a hobbit y la disyunción señala que 2 de ellos son el mismo individuo

Cuantificación + identidad HAY EXACTAMENTE DOS… • Se trata de combinar las ideas de ‘al menos’ y ‘como máximo’ Hay exactamente 2 hobbits quiere decir que: Hay al menos 2 hobbits Y hay como máximo 2 hobbits xy(Hx Hy x≠y) xyz((Hx Hy Hz) (x=y x=z y=z)) Esto se puede simplificar, haciendo que las variables x e y del caigan bajo el alcance del : xy[Hx Hy x≠y z(Hz (x=z y=z))]

Cuantificación + identidad OTRO Algunos orcos buscan a Frodo, pero han secuestrado a otro Frodo = a ser orco = O buscar = B secuestrar = S xy(Ox Bxa Sxy y ≠ a ) es decir, alguien es orco, ese alguien busca a Frodo, ese alguien (x) secuestra a “otro alguien” (y), y este último “alguien” no es Frodo. La idea de ‘otro’ viene recogida en y ≠ a

Cuantificación + identidad SÓLO Gollum piensa sólo en el Anillo Único Gollum = a el Anillo = b pensar en = P Consideremos: Pab Esta formalización dice que Gollum piensa en el Anillo, pero no capta el hecho de que Gollum no piensa en ninguna otra cosa. Esto podemos expresarlo con la identidad: Pab x(Pax x=b) es decir: cualquier cosa en la que piense Gollum, ha de ser el Anillo

Cuantificación + identidad SÓLO Sólo Gollum piensa en el Anillo Único Gollum = a el Anillo = b pensar en = P Las cosas han cambiado: la restricción lógica que impone la partícula SÓLO apunta hacia otro elemento: Pab x(Pxb x=a) es decir: el conjunto de los que piensan en el Anillo se reduce a Gollum

Cuantificación + identidad SÓLO Frodo ama a Sam Sólo Frodo ama a Sam Frodo ama sólo a Sam Frodo es el único que ama sólo a Sam Aab x(Axb x=a) Aab x(Aax x=b) Aab x(Aax x=b) x(Axb y(Axy y=b)) x=a)

Cuantificación: sólo vs. todos • SÓLO no siempre se expresa recurriendo al símbolo de identidad. Cuando expresamos relaciones entre grupos por medio de un condicional, debemos tener en cuenta en qué dirección se establece dicha relación. Esto es pertinente al comparar sólo con todos: 1. Todos los enanos son avaros x(Nx Ax) 2. Sólo los enanos son avaros x(Ax Nx) 1 dice que si uno es enano, entonces es avaro, pero puede ser que otras criaturas también sean avaras 2 excluye esta última posibilidad: si una criatura es avara, entonces esa criatura es un enano

Cuantificación: sólo vs. todos • 1. La partícula SÓLO puede aparecer en una posición diferente, relacionando grupos de individuos: Sólo los enanos desprecian a los elfos xy((Ey Dxy) Nx) xy(Ey (Dxy Nx)) Si uno es elfo y es despreciado, quien lo desprecia es un enano 2. Los enanos desprecian sólo a los elfos xy((Nx Dxy) Ey) xy(Nx (Dxy Ey)) Si uno es enano y desprecia a alguien, ese a quien desprecia es un elfo Compárese con Los enanos desprecian a los elfos: xy((Nx Ey) Dxy) xy(Nx (Ey Dxy))

Cuantificación: sólo vs. todos • Las restricciones que establecen SÓLO y TODOS pueden combinarse en oraciones como 1. Los enanos desprecian a los elfos, y sólo a ellos xy(Nx (Ey Dxy)) xy(Nx (Dxy Ey)) lo cual equivale a: xy(Nx (Ey Dxy)) es decir, si uno es enano, todo el que desprecia es elfo y todo el que es elfo es despreciado por él 2. Los enanos, y sólo ellos, desprecian a los elfos xy(Nx (Ey Dxy)) xy(Ey (Dxy Nx)) lo cual equivale a: xy(Ey (Nx Dxy))

Más ejemplos de formalización Alfonsina es hermana de Blasa si y sólo si Blasa es hermana de Alfonsina: Hab Hba Todos envidian al Papa: x. Exa Bush desprecia a todo el mundo: x. Dax

Más ejemplos de formalización Alguien vive en Andorra: x. Vxa Liechtenstein está en alguna parte: x. Eax Algunos americanos votaron a Bush: x (Ax Vxb) Todos los suizos votaron a Bush: x (Sx Vxb)

Más ejemplos de formalización Ningún demócrata votó a Bush: ¬ x(Dx Vxb) o también: x(Dx ¬Vxb) Algunos envidian a los búlgaros: x y(By Exy) Los búlgaros imitan a los griegos: xy((Bx Gy) Ixy)

Más ejemplos de formalización (Sacados de M. Manzano y A. Huertas): Alicia no ama a nadie, ni a sí misma, pero Benigno, que es enfermero, la ama x¬Aax ¬Aaa Eb Aba Benigno le habla a Alicia, pero ella no habla con aquellos que la aman, ni con nadie Hba x(Axa ¬Hax) x¬Hax

Más ejemplos de formalización Alicia es amada pero sólo le hablan los que confían en Benigno x. Axa x(Hxa Cxb) o también: . . . x(¬Cxb ¬Hxa) Los otros enfermeros no le hablan a Alicia y desconfían de Benigno x ((Ex x≠b) (¬Hxa ¬Cxb)) (desconfiar = no confiar)

Más ejemplos de formalización Lanzarote ama a Ginebra, pero ella no ama a todos los que la aman Aab ¬ x(Axb Abx) Lanzarote no ama a ninguno de sus amigos x(Mxa ¬Aax) Los amigos de Lanzarote no aman a aquellos a quienes Lanzarote ama xy(Mxa (Aay ¬Axy))

Más ejemplos de formalización Únicamente los cocineros famosos se admiran a sí mismos x(Axx (Cx Fx)) o también: x(¬(Cx Fx) ¬Axx) No todos los cocineros que viven en Donostia admiran a los cocineros famosos: ¬ xy([Cx Vxa] [(Cy Fy) Axy]) o también: xy(Cx Vxa Cy Fy ¬Axy)
 Lgica
Lgica Lgica
Lgica Lgica
Lgica Condicional asociado
Condicional asociado Lgica
Lgica Enunciado proposicional ejemplos
Enunciado proposicional ejemplos Lgica
Lgica Lgica
Lgica Tipo de entrevistas
Tipo de entrevistas Lukis
Lukis Tema-tema teologi perjanjian lama
Tema-tema teologi perjanjian lama Delimitación del problema ejemplo
Delimitación del problema ejemplo Subtema
Subtema Comunicacin escrita
Comunicacin escrita Lenguaje algebraico ejemplos
Lenguaje algebraico ejemplos Lenguaje algebraico y resolución de ecuaciones
Lenguaje algebraico y resolución de ecuaciones Lenguaje verbal a lenguaje algebraico
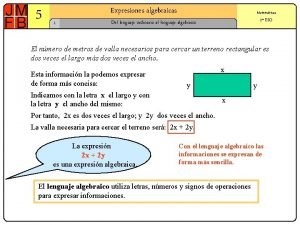
Lenguaje verbal a lenguaje algebraico Lenguaje ordinario y lenguaje algebraico
Lenguaje ordinario y lenguaje algebraico Tungkol saan ang tulang sa dalampasigan
Tungkol saan ang tulang sa dalampasigan Examples of grammatical competence
Examples of grammatical competence Prédicas sobre el matrimonio y la familia
Prédicas sobre el matrimonio y la familia Tema triduo pascual
Tema triduo pascual Observacion de un tema
Observacion de un tema Sermon tematico
Sermon tematico Tema e problema
Tema e problema Savaites tema pavasaris
Savaites tema pavasaris Tekstet argumentuese
Tekstet argumentuese Notturno ujević
Notturno ujević Qual é o tema do mapa
Qual é o tema do mapa La importancia del evangelismo
La importancia del evangelismo Tema mpls
Tema mpls Tema el amor del padre
Tema el amor del padre Isda ko sa mariveles nasa loob ang kaliskis
Isda ko sa mariveles nasa loob ang kaliskis Contoh topik penelitian
Contoh topik penelitian Kualitatif dan kuantitatif maksud
Kualitatif dan kuantitatif maksud Estructura interna y externa de un anuncio publicitario
Estructura interna y externa de un anuncio publicitario Mapanghikayat na pagsulat kahulugan
Mapanghikayat na pagsulat kahulugan Cuadro comparativo de la celestina y don quijote
Cuadro comparativo de la celestina y don quijote Tema sui malavoglia
Tema sui malavoglia Sentence of reach
Sentence of reach Tema is
Tema is Valaská škola mravúv stodola tema
Valaská škola mravúv stodola tema Nyere ungdomslitteratur
Nyere ungdomslitteratur Mision de la iglesia
Mision de la iglesia Sretni princ i druge bajke analiza
Sretni princ i druge bajke analiza Esquema sobre la fe
Esquema sobre la fe