Tema 3 Del Clculo Diferencial a las Ecuaciones

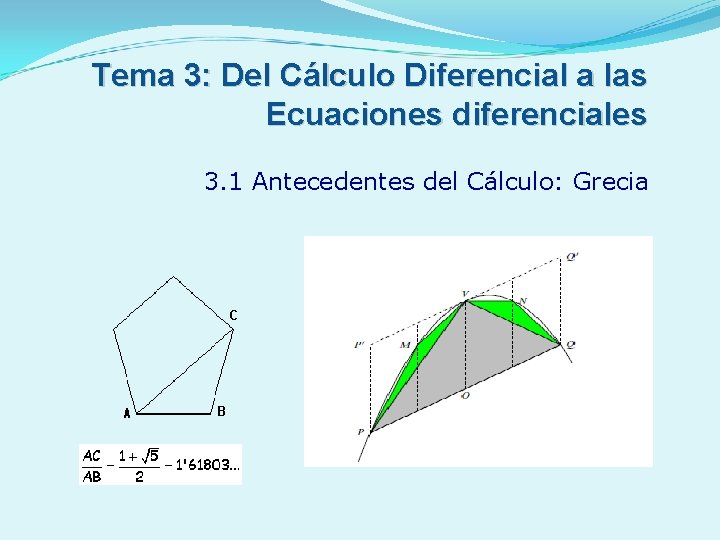
Tema 3: Del Cálculo Diferencial a las Ecuaciones diferenciales 3. 1 Antecedentes del Cálculo: Grecia

La razón aúrea Los segmentoss coloreados del pentagrama poseen proporciones áureas. Teniendo en cuenta la gran simetríade este símbolo, se observa que dentro del pentágono interior es posible dibujar una nueva estrella, de forma recurrente. Del mismo modo, es posible dibujar un pentágono por el exterior, que sería a su vez el pentágono interior de una estrella más grande. En este proceso de construcción, ¿existirá un pentágono tan diminuto que no pueda construirse otro más pequeño?

Tema 3: Del Cálculo Diferencial a las Ecuaciones diferenciales 3. 1 Antecedentes del Cálculo: Grecia. 3. Procesos Infinitos En su estudio de la materia los griegos se hicieron la pregunta fundamental: ¿se puede dividir de forma continua la materia en trozos más y más pequeños o se alcanza una pieza tan diminuta que no puede dividirse aún más? 1. Pitagóricos 2. Parménides y la escuela Eleática. Paradojas de Zenón 3. Demócrito y el atomismo.

Pitagóricos Los pitagóricos habían supuesto que el espacio y el tiempo pueden ser imaginados como constituidos por puntos e instantes. Los elementos últimos que forman una pluralidad se suponían, por una parte, que tenían las características de la unidad geométrica, el punto, y por otra las características de las unidades numéricas o de los números. Una proporción entre dos segmentos es una cantidad que a veces puede expresarse con ayuda de números. (si bien éstos- racionales-no eran suficientes para expresar la proporción entre ciertos segmentos. )

Parménides (510 -450 a. C. ) y la escuela eleática 1. Parménides distingue entre la apariencia y la esencia de las cosas. 2. El cambio y el movimiento son mera ilusión. h 3. El espacio, el tiempo, … son indivisibles: porque el vacío que separaría las partes sería el no-ser, y el no-ser no es. 4. La ciencia ha de buscar esa realidad detrás de las apariencias del mundo de los sentidos y distinguir la verdad (el ser) de la opinión (el no ser).

Zenón de Elea (siglo IV a. C. ) Método dialéctico: partir de las premisas que defiende el oponente para terminar reduciéndolas al absurdo. Las aporías de Zenón son un extraordinario desafío, al que filósofos y matemáticos han dado diversas respuestas, sin que aún hoy se tenga conciencia clara de haberlas podido explicar de forma totalmente convincente.

Zenón de Elea (siglo IV a. C. ) Dicotomía: Afirma que antes de que un objeto en movimiento pueda recorrer una distancia dada, debe recorrer en primer lugar la mitad de esta distancia, pero aún antes de recorrer un primer cuarto de la mitad inicial , …y así indefinidamente, a través de una cantidad infinita de subdivisiones. El corredor que quiere iniciar su carrera debe realizar un número infinito de etapas sin ninguna primera en un tiempo finito, y, por lo tanto el mismo comienzo del movimiento es imposible.

Zenón de Elea (siglo IV a. C. ) Aquiles y la tortuga. Aquiles deja una distancia inicial a la tortuga. Cuando Aquiles llega a la posición inicial de la tortuga ésta se encuentra en una posición más avanzada, cuando el primero llega a esta posición la tortuga se encuentra en una tercera posición, y así e proceso continúa indefinidamente, con el resultado de que el veloz Aquiles permanece corriendo sin alcanzar jamás a la tortuga que le lleva unos pocos metros de ventaja.

Zenón de Elea (siglo IV a. C. ) Flecha disparada: Si se supone que el espacio y el tiempo están formados por unidades mínimas indivisibles y el movimiento es una sucesión de diminutos saltos consecutivos, en cada uno de esos instantes indivisible de tiempo, la flecha. debe permanecer quieta. Por tanto, en cada instante la flecha está quieta y, como el tiempo se compone de instantes, la flecha está siempre quieta y el movimiento no tiene lugar.

Demócrito (460 - 370 a. C. ) y el atomismo físico Los atomistas mantienen que hay dos principios fundamentales: los átomos y el vacío. Niegan la infinita divisibilidad del espacio y la materia y afirman que cualquier magnitud contiene elementos últimos indivisibles: los átomos (significa lo que no puede dividirse). Los átomos son invisibles, infinitos en número y de diversas formas y tamaños, perfectamente sólidos, indestructibles y permanentes.

Demócrito y el atomismo físico Argumento: Si una magnitud continua fuera dividida en todo punto, entonces no quedaría nada o sólo quedarían puntos sin extensión, porque en caso contrario el proceso de división podría proseguir. Si quedan puntos sin extensión, entonces no es posible recomponer la magnitud original a partir de ellos, pues por la agregación de puntos sin extensión no puede lograrse nunca una magnitud finita.

Aristóteles (384 -322 a. C. ) Refutación: Una magnitud continua puede ser dividida en cualquier punto, pero no puede ser dividida en todo punto. Para Aristóteles, dividir un continuo en todos sus puntos es reducirlo a lo discreto. Mientras que un continuo tiene la propiedad de densidad, es decir, entre dos cualesquiera de sus puntos siempre hay otro punto del continuo y si dividimos un continuo en cualquier punto, lo que obtenemos son dos continuos cada uno de ellos con la propiedad de densidad.

El Infinito y más allá El infinito, como el espacio, es uno de los conceptos matemáticos que entran de lleno en el terreno de la filosofía. Ambos atañen a la percepción del mundo, por lo que no es de extrañar que la evolución del infinito, como objeto matemático, haya estado muy unida a su concepción filosófica. Anaximandro (ca. 610 - 546 a. C. ) introdujo el infinito en la filosofía Griega como el ápeiron que significa etimológicamente lo sin límites.

'La interacción de filosofía y matemáticas en raras ocasiones se revela con tanta claridad como en el estudio del infinito entre los antiguos griegos. Los enigmas dialécticos de los Eleáticos del siglo V, refinados por Platón y Aristóteles en el siglo IV, son complementados con la invención de métodos precisos de límites, como los aplicados por Eudoxo en el siglo IV, Euclides y Arquímedes en el III'.

El Infinito y más allá La introducción de conjuntos o procesos infinitos es la causa principal de la aparición de paradojas en Matemáticas. Los matemáticos griegos fueron plenamente conscientes de este fenómeno, lo que les llevó a una autolimitación en el uso infinito.

Aristóteles (384 -322 a. C. ) El principio de no contradicción, según el cual una proposición y su negación no pueden ser ambas verdaderas al mismo tiempo y en el mismo sentido.

Aristóteles termina estableciendo en su Libro III de su Física, dos clases diferentes de infinito: el infinito potencial y el infinito actual. Entiende el infinito potencial, como un proceso constante , secuencial de adición o de subdivisión sin final. El infinito actual potencial nunca será plenamente realizado: pues no hay un infinito tal que después sea en acto.

Aristóteles El infinito actual está concebido como obra terminada y cuya existencia niega. (nunca será plenamente realizado). metáfora : el ser de un día es un estar siendo de forma sucesiva, de manera que en ningún momento el día queda realizado plenamente como un todo. Decimos que el infinito “es” en el sentido en que decimos “el día es”.

Aristóteles Tener la posibilidad de hacerlo define el infinito potencial; tenerlo hecho, el infinito actual. Decir que la serie de los números naturales 1, 2, 3, 4, … es infinita, significa que: dado cualquier número N siempre podremos crear un siguiente número que será N + 1, pero… nadie puede construir toda la serie.

Pies de plomo 1. Euclides, en sus famosos Elementos, cuando se refiere a rectas habla de “segmentos cuya longitud la podemos hacer todo lo larga queramos”, en una clara alusión al infinito potencial, pero no dirá “rectas infinitas”. Igualmente, al enunciar que los números primos son infinitos, lo expresa diciendo que “Hay más números primos que cualquier cantidad de números primos propuesta”. De esta forma evita considerar el infinito actual de los números primos.

Más atrevido Arquímedes, hace un uso muy libre del infinito: descompone volúmenes como sumas infinitas de secciones, es decir, reduce un continuo a elementos indivisibles. Da nuevo vigor a los atomistas y anticipa el principio de Cavalieri.

Aplicaciones El volumen de la pirámide es un tercio del producto del área de la base por la altura. 2. Un prisma triangular puede descomponerse en tres pirámides triangulares que tienen, dos a dos, igual altura e igual área de la base, 3 Dos pirámides de bases y alturas iguales descompuestas en una cantidad infinita de secciones transversales infinitamente delgadas y en correspondencia biunívoca,

El método exhaustivo aunque consiste en una aproximación al área seguida e incluso su nombre sugiere “agotamiento” de una figura plana por polígonos inscritos no es un proceso límite. El método, como ya hemos indicado, estaba basado en un razonamiento muy cuidadoso de doble reducción al absurdo (razonamiento apagógico), precisamente para evitar la consideración de un infinito actual.