Tema 1 Nombres complexos lgebra i Geometria EETAC

Tema 1. Nombres complexos Àlgebra i Geometria. EETAC Susana-Clara López 1

Nombres complexos Introducció. Forma binòmica. - Part real i part imaginària Operacions Pla complex. Forma exponencial - Fórmula d’Euler Operacions Càlcul d’arrels n-èssimes Descomposició factorial. - Teorema fonamental de l’àlgebra - Fórmules trigonomètriques Annex. 2

Introducció Equacions sense solució (en els reals): Introduïm complint 3

Definició. Operacions Un nombre complex: z = (a, b) on a, b nombres reals. SUMA: (a, b) + (c, d) = (a + c, b + d) PRODUCTE: (a, b) · (c, d) = (ac - bd, ad + bc) exemple: (0, 1) · (0, 1) = ( -1, 0) 4

Extensió dels reals El conjunt dels nombres complexos es denota C És una. extensió dels nombres reals a s’identifica amb el complex (a, 0) i les operacions: a + c = (a, 0) + (c, 0) = (a+c, 0) a · c =(a, 0) · (c, 0) = (ac, 0) També: a · (c , d) = (a, 0) · (c , d)= (ac, ad) 5

Forma binòmica z = (a, b) = = (a, 0) + (0, b) = a (1, 0)+ b (0, 1)= = a + bj On j = (0, 1) compleix j 2 = (-1, 0)=-1 a = Re (z) part real; b= Im (z) part imaginària exemples: Real : Im (z) =0 Imaginari pur : Re (z) =0 6

Operacions en forma binòmica SUMA: PRODUCTE: exemples: 7

Oposat. Conjugat. Invers L’oposat de z = a +bj és –z = - a – bj, d’on El conjugat de z = a +bj és z = a – bj, d’on : i l’invers de z = a +bj és z-1= (a – bj)/(a 2 + b 2), d’on 8

El cos dels nombres C - (C, +) són un grup commutatiu: associativa, commutativa, element neutre (0, 0), cada element (a, b) té el seu oposat (-a, -b) - (C, ·) són un semigrup commutatiu: associativa, commutativa, element neutre (1, 0), cada element (a, b)≠(0, 0) té el seu invers (a, b) -1=(a/(a 2 + b 2), -b/(a 2 + b 2)) - Distributiva del producte respecte la suma 9

Pla complex. Forma Exponencial Un nombre complex z = a + bj = (a, b) R = |z| =>Mòdul de z α = arg(z) => Argument de z, (l’angle amb l’eix real) Reαj és la forma exponencial de z 10
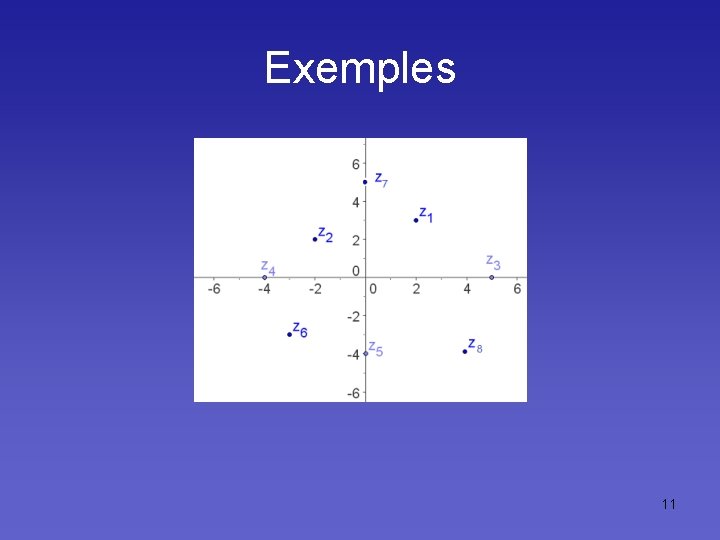
Exemples 11

Propietats z i z tenen el mateix mòdul, i l’ argument de signe contrari. És a dir, z= Reαj z=Re- αj També: (i) z · z =|z|2 (ii) z+z=2 Re (z) (iii) z-z=2 j Im (z) L’argument no és únic (està definit mòdul 2π) Argument principal: 0 < α < 2π 12

Fórmula d’Euler La fórmula d’Euler, donat α real, La forma exponencial d’un complex de mòdul R i argument α és a dir, 13

Operacions en forma exponencial PRODUCTE: D’aquí - l’invers - la divisió - les potències 14

Càlcul d’arrels n-èssimes Definició: Càlcul: on representa l’arrel real positiva 15

Exemples • Resoleu: a) b) c) d) e) z 3 – 8 = 0 z 3 + 5 = 0 z 4 = 2 z 4 + 1 = 0 z 3 = – 2+2 j 16

Càlcul d’arrels n-èssimes Propietats: 1. Les arrels n-èssimes de z són els vèrtexs d’un polígon regular de n costats amb centre en l’origen. 2. La suma de les arrels n-èssimes de z és zero i el seu producte és (-1) n-1·z 17

Polinomis a coeficients en R i C Un polinomi de variable z a coeficients en els reals (o en els complexos): són els coeficients reals o complexos el grau del polinomi (el polinomi nul, no té grau) polinomi mònic 18

Operacions Donats SUMA: PRODUCTE: Propietats: 1. 2. 19

Divisibilitat i arrels. Teorema d’Euclides: Si r (z)=0, diem que b(z) és un divisor de a(z). Arrels de polinomi: α és una arrel de p si p(α)=0 Proposició. α és una arrel de p si i només si (z- α) és un divisor de p. α és una arrel de multiplicitat m de p, si (z- α) m és un divisor de p, pero (z- α) m+1 no ho és. Ex z 3 -3 z+2=(z-1)2(z+2) 20

Teorema fonamental de l’àlgebra Tot polinomi a coeficients en els complexos, amb grau > 1 té almenys una arrel complexa. Corol·lari. Tot polinomi P amb grau(P) =n té n-arrels α 1, α 2, …, αn. i la descomposició factorial en els complexos 21

Exemples • Trobeu la descomposició a C dels polinomis següents: a) z 2 – 5 z + 6 b) z 2 + 3 jz – 2 c) z 4 + 1 22

Propietats 1. Si tots els coeficients de p són reals: α és arrel de multiplicitat m de p <=> α és arrel de multiplicitat m de p 2. Tot polinomi a coeficients reals descomposa en factors de grau 1 o 2 en R[x] (z – α)·(z – α) =z 2 -(α+ α)z+|α|2 3. I la descomposició factorial en els reals on per a tot j 23

Exemples • Trobeu la descomposició a C dels polinomis següents: a) b) c) d) 2 z 2 + 5 z – 3 z 5 – 2 z 4 + z – 2 z 4 + 2 z 2 +1 z 4 + 1 • Sabent que – 1+2 j és arrel de z 4 + 2 z 3 +9 z 2 +8 z + 20, trobeu la resta d’arrels i la descomposició factorial a R i a C 24

Annex: Fórmules trigonomètriques 25

Fórmules trigonomètriques. Fórmula de Moivre El producte: en termes de sinus i cosinus: De les potències: (Fórmula de Moivre) 26

Fórmules trigonomètriques De la fórmula d’Euler: L’extensió de l’exponencial: en particular, 27
- Slides: 27