TELIN Estimation and detection from coded signals Overview

TELIN Estimation and detection from coded signals Overview of research at UGent (37) and cooperation with NEWCOM partners Marc Moeneclaey, UGent - TELIN dept. Marc. Moeneclaey@telin. UGent. be 1

Outline TELIN • Coding + linear modulation, AWGN channel • MAP detection * carrier phase and timing known * carrier phase and timing unknown • ML synchronization * Cramer-Rao bound, modified Cramer-Rao bound * expectation-maximization (EM) algorithm • Numerical results • Related research (channel estimation, OFDM, MIMO, CDMA, multipath fading, time-varying parameters, . . . ) • Cooperation with NEWCOM partners 2

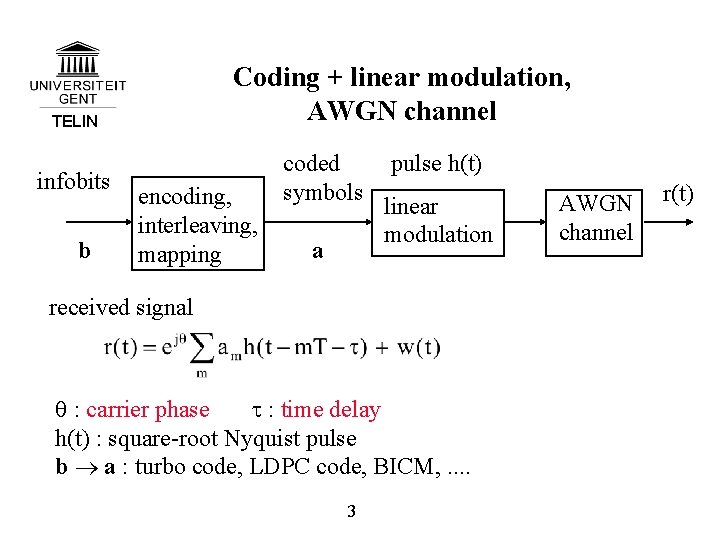
Coding + linear modulation, AWGN channel TELIN infobits b encoding, interleaving, mapping coded symbols a pulse h(t) linear modulation received signal q : carrier phase t : time delay h(t) : square-root Nyquist pulse b a : turbo code, LDPC code, BICM, . . 3 AWGN channel r(t)

MAP detection, (q, t) known (1/2) TELIN MAP detection (on individual infobits) achieves minimum BER r : vector representation of r(t) Assuming (q, t) = (q 0, t 0) is known, APP is given by (many terms !) Summation over information sequences can be done efficiently (message-passing in factor graph of encoder+interleaver+mapper) 4

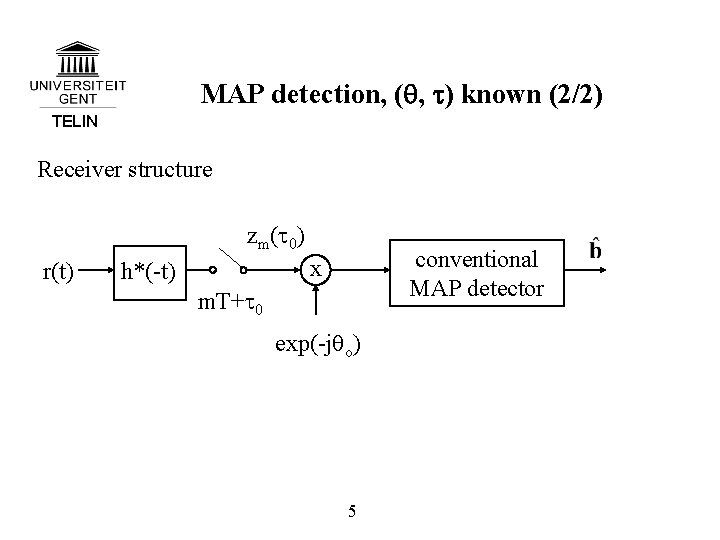
MAP detection, (q, t) known (2/2) TELIN Receiver structure zm(t 0) r(t) conventional MAP detector x h*(-t) m. T+t 0 exp(-jqo) 5

MAP detection, (q, t) unknown TELIN When (q, t) is unknown, APP is given by conventional MAP detector hard to compute, because of integration over (q, t) we look for a (suboptimum) alternative 6

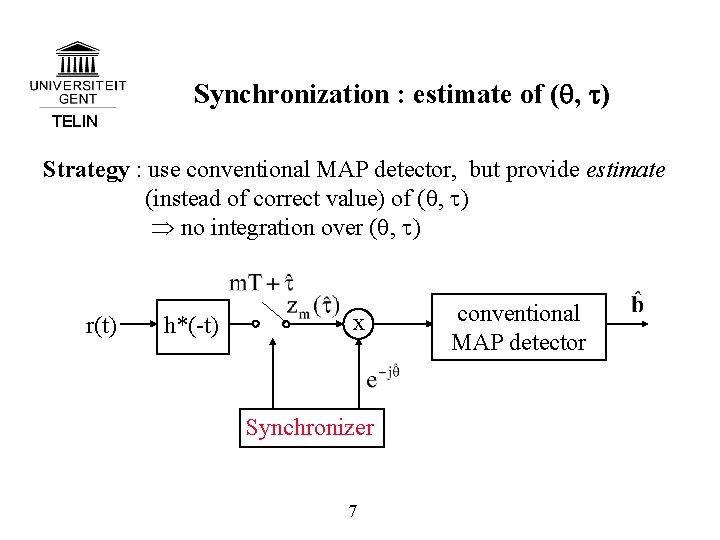
Synchronization : estimate of (q, t) TELIN Strategy : use conventional MAP detector, but provide estimate (instead of correct value) of (q, t) no integration over (q, t) r(t) h*(-t) x Synchronizer 7 conventional MAP detector

ML synchronization TELIN ML estimation of (q, t) : no integrations required, but sum contains many terms that are function of (q, t) ML estimate hard to compute (2 -D search) 8

Cramer-Rao lower bound (1/2) TELIN Motivation for ML estimation : for long observation intervals, mean-square estimation error (MSEE) converges to Cramer-Rao lower bound (CRB) on MSEE When the data symbols are not a priori known to the receiver, computation of the CRB is hard, especially for coded transmission. A simpler but less tight bound is the modified CRB (MCRB), which basically assumes that the data symbols are known to the receiver 9

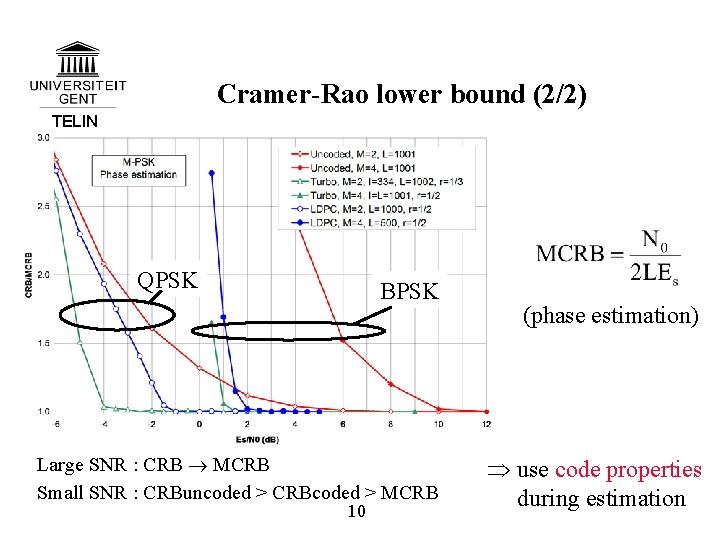
Cramer-Rao lower bound (2/2) TELIN QPSK BPSK Large SNR : CRB MCRB Small SNR : CRBuncoded > CRBcoded > MCRB 10 (phase estimation) use code properties during estimation

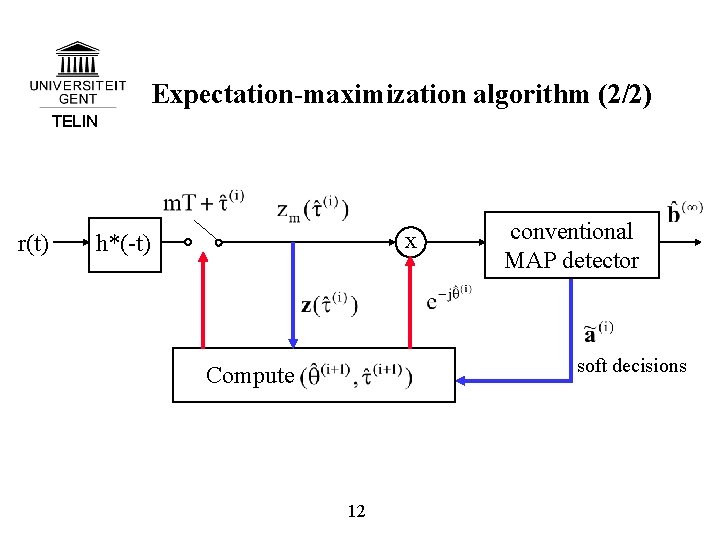
Expectation-maximization algorithm (1/2) TELIN Direct application of ML estimation is complicated. ML estimate can be obtained iteratively by means of EM algorithm soft symbol decision : requires APPs of symbols (by-product of MAP detector) 11

Expectation-maximization algorithm (2/2) TELIN r(t) x h*(-t) conventional MAP detector soft decisions Compute 12

Convergence behavior of EM algorithm TELIN phase estimation error at i-th iteration : negative zero-crossings : stable positive zero-crossings : unstable 13

Convergence behavior of EM algorithm TELIN phase estimation error at i-th iteration : initialization is critical acquisition range 14

Initialization of EM algorithm (1/4) TELIN • DA initialization (pilot symbols) : - consumes power and bandwidth resources - does not exploit unknown data symbols (many pilot symbols needed) • NDA initialization (O&M for timing, V&V for phase) - gives rise to phase and timing ambiguities 15

Initialization of EM algorithm (2/4) TELIN Proposed solution - Different initializations, e. g. , - Parallel EM algorithms with different initializations, each running for only one (or a few) iterations - Continue with the EM algorithm that gave the largest maximum in the maximization step after one (or a few) iterations 16

Initialization of EM algorithm (3/4) TELIN Example 1 : phase estimation, QPSK (perfect ambiguity resolution) other equil. points 17

Initialization of EM algorithm (4/4) TELIN Example 2 : phase estimation and ambiguity resolution, QPSK other equil. points 18

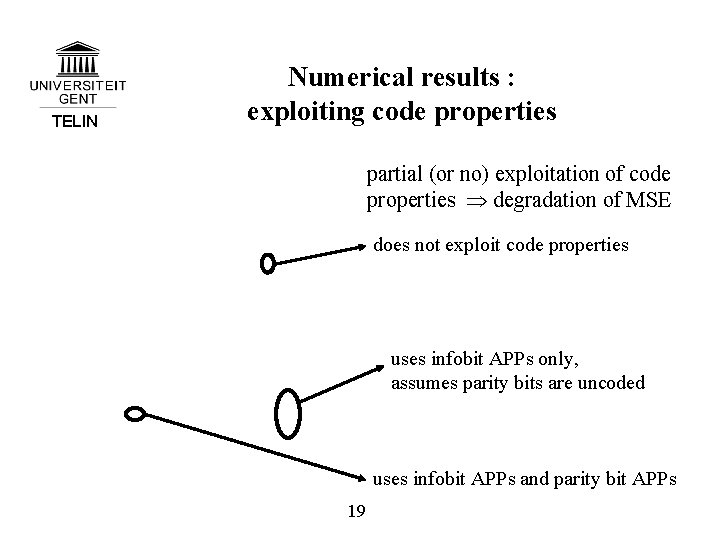
TELIN Numerical results : exploiting code properties partial (or no) exploitation of code properties degradation of MSE does not exploit code properties uses infobit APPs only, assumes parity bits are uncoded uses infobit APPs and parity bit APPs 19

Numerical results : phase estimation (1/2) TELIN 20

Numerical results : phase estimation (2/2) TELIN 21

TELIN Numerical results : phase estimation + ambiguity resolution 22

Numerical results : timing estimation (1/2) TELIN 23

Numerical results : timing estimation (1/2) TELIN 24

TELIN Numerical results : timing estimation + frame synchronization 25

Related research at UGent TELIN Extension of phase and timing estimation from linear modulation transmitted over AWGN channel to the following : • • • Carrier frequency estimation and channel estimation Multiuser CDMA, OFDM, UWB Multipath fading channel, MIMO channel Multidimensional mapping + optimization Estimation of time-vaying parameters by means of iterative feedback algorithm • etc. 26

Cooperation within NEWCOM (1/3) TELIN joint papers on EM-based parameter estimation • EURASIP JWCN paper accepted UGent + UCL(Vandendorpe) + Uo. P(Luise) • ISSSTA’ 04 UCL(Vandendorpe) + UGent • IEEE Trans. Comm. paper submitted UCL(Vandendorpe) + UGent • Lecture notes in Computer Science, 2004 ETH(Loeliger)+UGent 27

Cooperation within NEWCOM (2/3) TELIN joint papers on estimation of time-varying parameters • EUSIPCO 2005 paper submitted ISIK(Panayirci) + UGent • Globecom 2005 paper submitted ISIK(Panayirci) + UGent 28

Cooperation within NEWCOM (3/3) TELIN UGent would like to • Continue existing cooperations • Enter new cooperations Broad topic : “estimation and detection from coded signals” Type of cooperation : • Joint publications • Joint research projects • etc. 29

Joint publications (1/2) TELIN 1) C. Herzet, H. Wymeersch, L. Vandendorpe and M. Moeneclaey , "On Maximum-Likelihood Timing Estimation", Submitted to IEEE Transactions on Communications. Joint UCL(038) - UGent (037) contribution 2) N. Noels, V. Lottici, A. Dejonghe, H. Steendam, M. Moeneclaey, M. Luise , L. Vandendorpe, "A Theoretical Framework for Soft Information Based Synchronization in Iterative (Turbo) Receivers”, accepted by EURASIP Journal on Wireless Communications and Networking Joint UGent(37)-UCL (38)- Uo. P (13) contribution 3) Ramon V. , Herzet C. , Vandendorpe L. and Moeneclaey M. , "EM algorithm-based estimation of amplitude, carrier phase and noise variance in multiuser turbo receivers", Proc. Eighth International Symposium on Spread Spectrum Techniques and Applications, 2004, ISSSTA 04, Sydney, Australia, Aug 30 - Sep 02 2004, pp. 550 - 554 Joint UCL (038)-UGent (037) contribution 30

Joint publications (2/2) TELIN 4) J. Dauwels, H. Wymeersch, H. -A. Loeliger and M. Moeneclaey "Phase Estimation and Phase Ambiguity Resolution by Message Passing", Telecommunications and Networking, Lecture Notes in Computer Science, vol. 3124, pp. 150 -155, Springer-Verlag, Berlin, 2004. Joint ETH(26)- UGENT(37) contribution 5) E. Panayirci, H. A. Cirpan and M. Moeneclaey, ”A Sequential Monte Carlo Method for Blind Phase Noise Estimation and Data Detection”, submitted to EUSIPCO 2005 Joint ISIK(07)-UGENT(37) contribution 6) E. Panayirci, H. A. Cirpan, M. Moeneclaey and N. Noels "Blind Data Detection in the presence of PLL phase noise by sequential Monte Carlo method”, submitted to Globecom’ 05 Joint ISIK(07)-UGENT(37) contribution 31