Tekstlesannete lahendamine vrrandi abil 9 klass lesanded 19

Tekstülesannete lahendamine võrrandi abil 9. klass ülesanded 19, 20, 25

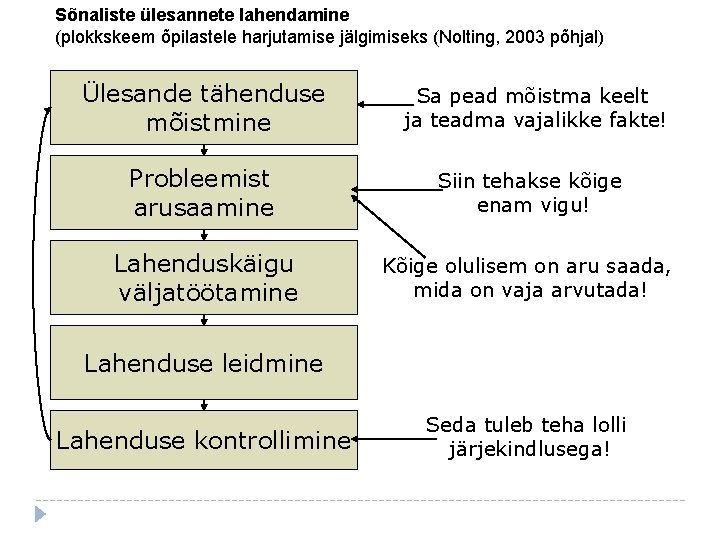
Sõnaliste ülesannete lahendamine (plokkskeem õpilastele harjutamise jälgimiseks (Nolting, 2003 põhjal) Ülesande tähenduse mõistmine Sa pead mõistma keelt ja teadma vajalikke fakte! Probleemist arusaamine Siin tehakse kõige enam vigu! Lahenduskäigu väljatöötamine Kõige olulisem on aru saada, mida on vaja arvutada! Lahenduse leidmine Lahenduse kontrollimine Seda tuleb teha lolli järjekindlusega!

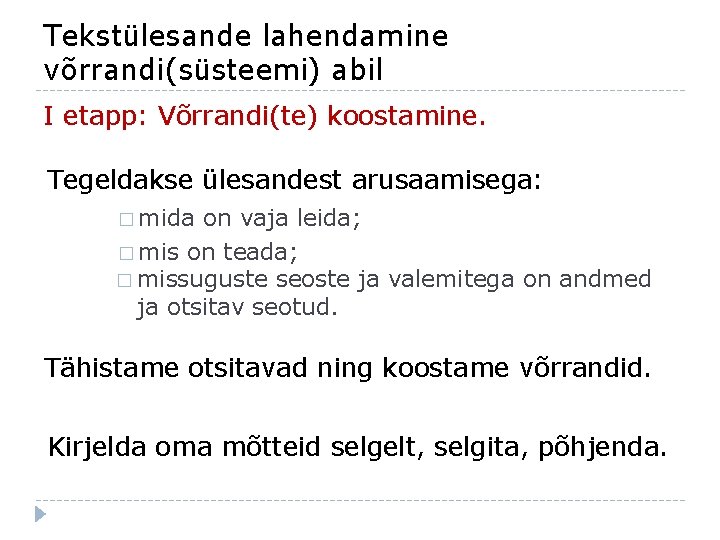
Tekstülesande lahendamine võrrandi(süsteemi) abil I etapp: Võrrandi(te) koostamine. Tegeldakse ülesandest arusaamisega: � mida on vaja leida; � mis on teada; � missuguste seoste ja valemitega on andmed ja otsitav seotud. Tähistame otsitavad ning koostame võrrandid. Kirjelda oma mõtteid selgelt, selgita, põhjenda.

Tekstülesande lahendamine võrrandi(süsteemi) abil II etapp: Võrrandi(süsteemi) lahendamine. Kas ülesande sisust tulenevalt on lahendite kohta eritingimusi? Näiteks lahendid peavad olema positiivsed lahendid peavad olema täisarvulised vms Lõpeb võrrandi(süsteemi) lahendi(te) välja kirjutamisega.

Tekstülesande lahendamine võrrandi(süsteemi) abil III etapp: Saadud tulemuste sisuline kontroll. Tulemuslause sõnastamine: “Sain, et …. ” Ülesande tingimuste kontroll: dubleerib võrrandi koostamise etappi, kuid nüüd juba olemasolevate andmetega. Kirjelda oma mõtteid selgelt, selgita, põhjenda. Lõpeb: “… nii nagu ülesandes nõutud. ”

Tekstülesande lahendamine võrrandi(süsteemi) abil IV etapp: Tekstülesande vastuse sõnastamine. Vastus täislausena Vastab täpselt küsimusele enne vastuse sõnastamist loe küsimus üle

Ül 19. Kui antud arvust nelja võrra suurem arv korrutada sellest nelja võrra väiksema arvuga ja lisada kolmekordne esialgne arv, siis saame 138. Leia see arv. Tähistame otsitava arvu tähega x. Sellest 4 võrra suurem arv on (x + 4); 4 võrra väiksem arv on (x – 4); Otsitava arvu 3 -kordne on 3 x. Koostame võrrandi ülesande teksti järgi: (x + 4)(x - 4)+ 3 x = 138.

Ül 19. Kui antud arvust nelja võrra suurem arv korrutada sellest nelja võrra väiksema arvuga ja lisada kolmekordne esialgne arv, siis saame 138. Leia see arv. Lahendan koostatud võrrandi. (x + 4)(x – 4) + 3 x = 138 X 2 – 16 + 3 x = 138 X 2+ 3 x – 154= 0 Avan sulud Viin vabaliikme vasakule ja koondan

Ül 19. Kui antud arvust nelja võrra suurem arv korrutada sellest nelja võrra väiksema arvuga ja lisada kolmekordne esialgne arv, siis saame 138. Leia see arv. Lahendan koostatud võrrandi. (x + 4)(x – 4) + 3 x = 138 x 2 – 16 + 3 x = 138 x 2+ 3 x – 154= 0 Avan sulud Viin vabaliikme vasakule ja koondan

Ül 19. Kui antud arvust nelja võrra suurem arv korrutada sellest nelja võrra väiksema arvuga ja lisada kolmekordne esialgne arv, siis saame 138. Leia see arv. x 2+ 3 x – 154= 0 a =1, b = 3, c = -154

Ül 19. Kui antud arvust nelja võrra suurem arv korrutada sellest nelja võrra väiksema arvuga ja lisada kolmekordne esialgne arv, siis saame 138. Leia see arv. Sain, et otsitav arv on -14 või 11. Kontroll. (II) (I) 11 Esialgne arv: – 14 15 – 10 4 võrra suurem: 7 4 võrra väiksem: – 18 33 3 -kordne: – 42 ülesande avaldis: (I) (-10)·(-18)+(-42) = 180+(-42)=138; (II) 15· 7 + 33 = 105 + 33=138. Otsitav arv on -14 või 11.

Ül 25. Rein luges raamatut. Ta luges iga päev võrdse arvu lehekülgi. Kui ta oleks lugenud 20 lk päevas vähem, oleks ta lõpetanud lugemise 3 päeva hiljem. Kui ta aga oleks lugenud 30 lk päevas rohkem, siis oleks tal raamatu lugemiseks läinud 2 päeva vähem. Mitu lk oli raamatus ja mitu lk luges Rein päevas? Tähistan Reinu tegeliku lugemistempo (lk/p) tähega x ning lugemisaja (p) tähega y. Siis loetud lehekülgede arv avaldub kujul x · y.

1) Kui Rein oleks lugenud 20 lk päevas vähem, so. (x – 20) lk, siis oleks ta lõpetanud lugemise 3 päeva hiljem, so (y + 3) päevaga. Loetud lk arv avaldub siis kujul (x - 20)(y + 3). 2) Kui Rein oleks lugenud 30 lk päevas rohkem, so. (x+30) lk, siis oleks tal raamatu lugemiseks läinud 2 päeva vähem, so (y – 2) päeva. Loetud lk arv avaldub siis kujul (x+30)(y - 2).

Et kõigil kolmel juhul on loetud lehekülgede koguarv sama, siis saan koostada võrrandid. (x - 20)(y + 3) = xy ja (x+30)(y - 2) = xy. Lihtsustan saadud võrrandeid. xy + 3 x - 20 y -60 = xy xy- 2 x+30 y - 60) = xy 3 x - 20 y = 60 - 2 x+30 y = 60 Lahendan liitmisvõttega.

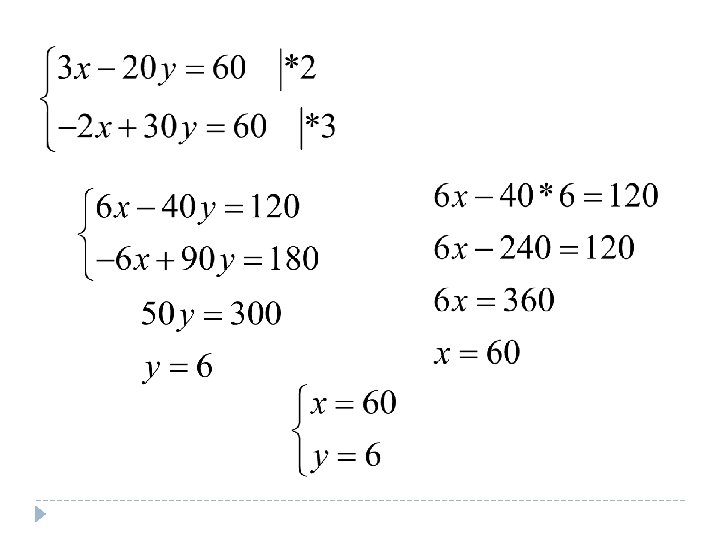
Sain, et Rein luges päevas 60 lk ning raamatus oli kokku 360 lk. Kui ta oleks lugenud päevas 60 – 20 = 40 lk, siis oleks aega kulunud 6 + 3 = 9 päeva. Raamatu lk arv on siis 9 * 40 = 360. Kui ta oleks lugenud päevas 60 + 30 = 90 lk, siis oleks aega kulunud 6 - 2 = 4 päeva. Raamatu lk arv on siis 4 * 90 = 360. Ülesande tingimused on täidetud. Vastus. Raamatus oli 360 lk, Rein luges päevas 60 lk.