Tehnici de sortare a tablourilor Structuri de date

Tehnici de sortare a tablourilor Structuri de date şi algoritmi -laborators. l. dr. ing. Ciprian-Bogdan Chirilă Universitatea Politehnica Timişoara 2014

Cuprins n n n Sortarea prin Sortarea prin Concluzii inserţie binară selecţie interschimbare amestecare

Sortarea prin inserţie Tabloul este împărţit în două subtablouri: n n tab[0], tab[1] , …, tab[i-1] - secvenţă sortată în care urmează să fie inserat tab[i]; tab[i], tab[i+1] , …, tab[n-1] - secvenţă nesortată, din care se extrag succesiv elemente ce vor fi înserate în secvenţa sortată;

Sortarea prin inserţie – demo 1 0 1 2 3 4 5 6 87 12 48 22 69 75 31 i=1 x=12 87 __ 48 22 69 75 31 87 > 12 ? da __ 87 48 22 69 75 31 insertie 12 87 48 22 69 75 31

Sortarea prin inserţie – demo 2 0 1 2 3 4 5 6 12 87 48 22 69 75 31 i=2 x=48 12 87 __ 22 69 75 31 87 > 48 ? da 12 __ 87 22 69 75 31 insertie 12 48 87 22 69 75 31

Sortarea prin inserţie – demo 3 0 1 2 3 4 5 6 12 48 87 22 69 75 31 i=3 x=22 12 48 87 __ 69 75 31 87 > 22 ? da 12 48 __ 87 69 75 31 48 > 22 ? da 12 __ 48 87 69 75 31 insertie 12 22 48 87 69 75 31

Sortarea prin inserţie – demo 4 0 1 2 3 4 5 6 12 22 48 87 69 75 31 i=4 x=69 12 22 48 87 __ 75 31 87 > 69 ? da 12 22 48 __ 87 75 31 insertie 12 22 48 69 87 75 31

Sortarea prin inserţie – demo 5 0 1 2 3 4 5 6 12 22 48 69 87 75 31 i=5 x=75 12 22 48 69 87 __ 31 87 > 75 ? da 12 22 48 69 __ 87 31 insertie 12 22 48 69 75 87 31

Sortarea prin inserţie binară n n n Principiul de funcţionare este cel descris anterior; Diferenţa apare la modalitatea de căutare a poziţiei unde se va insera elementul curent: căutare binară faţă de căutare liniară Apare un câştig de performanţă

Sortarea prin inserţie – demo 6 0 1 2 3 4 5 6 12 22 48 69 87 75 31 i=6 x=31 12 22 48 69 75 87 __ 87 > 31 ? da 12 22 48 69 75 __ 87 75 > 31 ? da 12 22 48 69 __ 75 87 69 > 31 ? da 12 22 48 __ 69 75 87 48 > 31 ? da 12 22 __ 48 69 75 87 insertie 12 22 31 48 69 75 87

Sortarea prin inserţie binară – demo 1 0 1 2 3 4 5 6 87 12 48 22 69 75 31 i=1 x=12 87 __ 48 22 69 75 31 s=0 __ 87 48 22 69 75 31 insertie 12 87 48 22 69 75 31

Sortarea prin inserţie binară – demo 2 0 1 2 3 4 5 6 12 87 48 22 69 75 31 i=2 x=48 12 87 __ 22 69 75 31 s=1 12 __ 87 22 69 75 31 insertie 12 48 87 22 69 75 31

Sortarea prin inserţie binară – demo 3 0 1 2 3 4 5 6 12 48 87 22 69 75 31 i=3 x=22 12 48 87 __ 69 75 31 s=1 12 __ 48 87 69 75 31 insertie 12 22 48 87 69 75 31

Sortarea prin inserţie binară – demo 4 0 1 2 3 4 5 6 12 22 48 87 69 75 31 i=4 x=69 12 22 48 87 __ 75 31 s=3 12 22 48 __ 87 75 31 insertie 12 22 48 69 87 75 31

Sortarea prin inserţie binară – demo 5 0 1 2 3 4 5 6 12 22 48 69 87 75 31 i=5 x=75 12 22 48 69 87 __ 31 s=4 12 22 48 69 __ 87 31 insertie 12 22 48 69 75 87 31

Sortarea prin inserţie binară – demo 6 0 1 2 3 4 5 6 12 22 48 69 75 87 31 i=6 x=31 12 22 48 69 75 87 __ s=2 12 22 __ 48 69 75 87 insertie 12 22 31 48 69 75 87

Sortarea prin selecţie n Se împarte tabloul în două: n n n Prima secvenţă este sortată; Pe a doua secvenţă se vor executa căutări repetate a elementului minim; Elementul minim găsit se va introduce în prima secvenţă;

Sortarea prin selecţie – demo 1 0 1 2 3 4 5 6 87 12 48 22 69 75 31 i=0 min=12 87 12 48 22 69 75 31 12 87 48 22 69 75 31

Sortarea prin selecţie – demo 2 0 1 2 3 4 5 6 12 87 48 22 69 75 31 i=1 min=22 12 87 48 22 69 75 31 12 22 48 87 69 75 31

Sortarea prin selecţie – demo 3 0 1 2 3 4 5 6 12 22 48 87 69 75 31 i=2 min=31 12 22 48 87 69 75 31 12 22 31 87 69 75 48

Sortarea prin selecţie – demo 4 0 1 2 3 4 5 6 12 22 31 87 69 75 48 i=3 min=48 12 22 31 87 69 75 48 12 22 31 48 69 75 87

Sortarea prin selecţie – demo 5 0 1 2 3 4 5 6 12 22 31 48 69 75 87 i=4 min=69 12 22 31 48 69 75 87

Sortarea prin selecţie – demo 6 0 1 2 3 4 5 6 12 22 31 48 69 75 87 i=5 min=75 12 22 31 48 69 75 87

Sortarea prin interschimbare n n Se parcurge şirul de la stânga la dreapta în mod repetat; La fiecare parcurgere se verifică succesiv dacă orice două elemente vecine sunt ordonate; Dacă nu sunt ordonate ele sunt interschimbate; Parcurgerile se repetă atât timp cât s-a găsit o pereche de elemente neordonate;

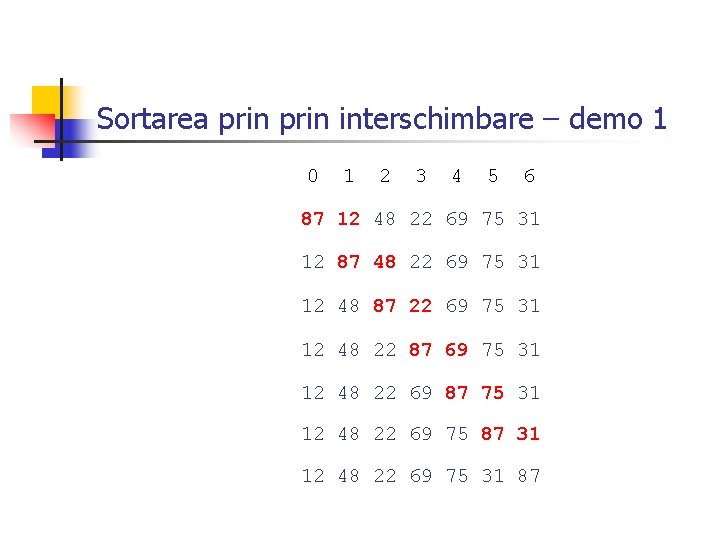
Sortarea prin interschimbare – demo 1 0 1 2 3 4 5 6 87 12 48 22 69 75 31 12 87 48 22 69 75 31 12 48 87 22 69 75 31 12 48 22 87 69 75 31 12 48 22 69 87 75 31 12 48 22 69 75 87 31 12 48 22 69 75 31 87

Sortarea prin interschimbare – demo 2 0 1 2 3 4 5 6 12 48 22 69 75 31 87 12 22 48 69 31 75 87

Sortarea prin interschimbare – demo 3 0 1 2 3 4 5 6 12 22 48 69 31 75 87 12 22 48 31 69 75 87

Sortarea prin interschimbare – demo 4 0 1 2 3 4 5 6 12 22 48 31 69 75 87 12 22 31 48 69 75 87

Sortarea prin amestecare n n Se menţine principiul de la sortarea anterioară; Se fac parcurgeri de la dreapta la stânga şi de la stânga la dreapta, în mod repetat; Plaja de elemente pe care sunt făcute parcurgerile se îngustează treptat Poziţia unde a avut loc ultima interschimbare va limita plaja de parcurgere şi superior şi inferior

Sortarea prin amestecare – cod 1 Sortare. Shaker. Sort(tab, n) j, k, l, r x l=1 r=n-1 k=n-1 fa { pentru j=r pana j>=l fa j-{ daca(tab[j-1]>tab[j]) { x=tab[j-1]=tab[j]=x k=j } } l=k+1

Sortarea prin amestecare – cod 2 pentru j=l pana j<=r fa j++ { daca(tab[j-1]>tab[j]) { x=tab[j-1]=tab[j]=x k=j } } r=k-1 } cat timp l<=r

Concluzii n toate sortarile prezentate au n n de regula doua cicluri for/while/do while imbricate de la 1 la n perfomanta O(n*n)