Tegangan Pembebanan dan Jenis Tegangan Bila suatu batang

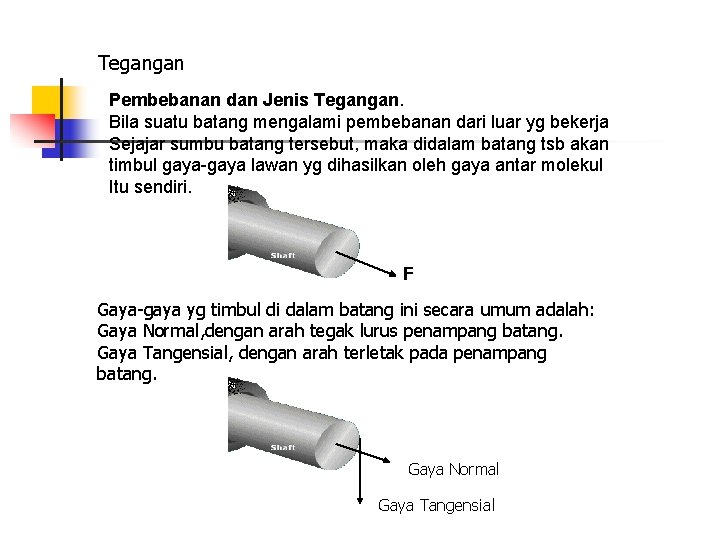
Tegangan Pembebanan dan Jenis Tegangan. Bila suatu batang mengalami pembebanan dari luar yg bekerja Sejajar sumbu batang tersebut, maka didalam batang tsb akan timbul gaya-gaya lawan yg dihasilkan oleh gaya antar molekul Itu sendiri. F Gaya-gaya yg timbul di dalam batang ini secara umum adalah: Gaya Normal, dengan arah tegak lurus penampang batang. Gaya Tangensial, dengan arah terletak pada penampang batang. Gaya Normal Gaya Tangensial

Dengan menganggap bahwa gaya-gaya yg timbul ini terbagi rata pada seluruh luas penampang, maka gaya-gaya yg bekerja pada suatu luasan penampang, disebut “ TEGANGAN” ( ). Gaya (F) Tegangan ( ) = Luas Penampang (A) Gaya (F) = Newton. Luas Penampang (A) = cm 2 atau mm 2. Tegangan ( ) = N/ cm 2 atau N/mm 2.

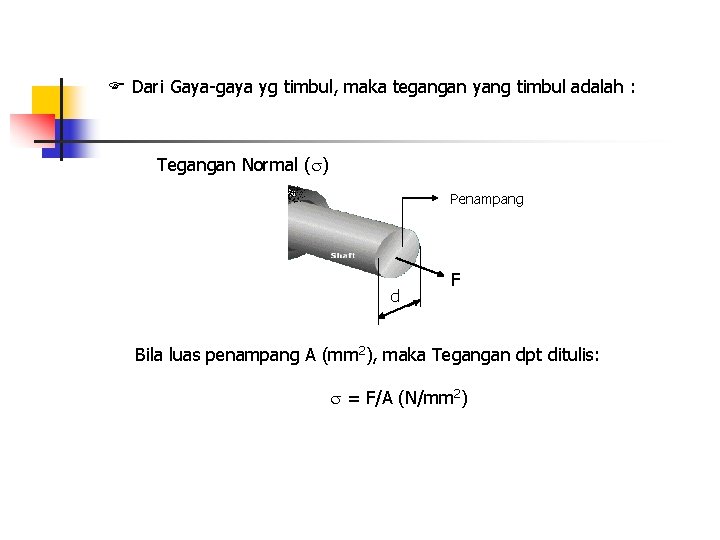
Dari Gaya-gaya yg timbul, maka tegangan yang timbul adalah : Tegangan Normal ( ) Penampang d F Bila luas penampang A (mm 2), maka Tegangan dpt ditulis: = F/A (N/mm 2)

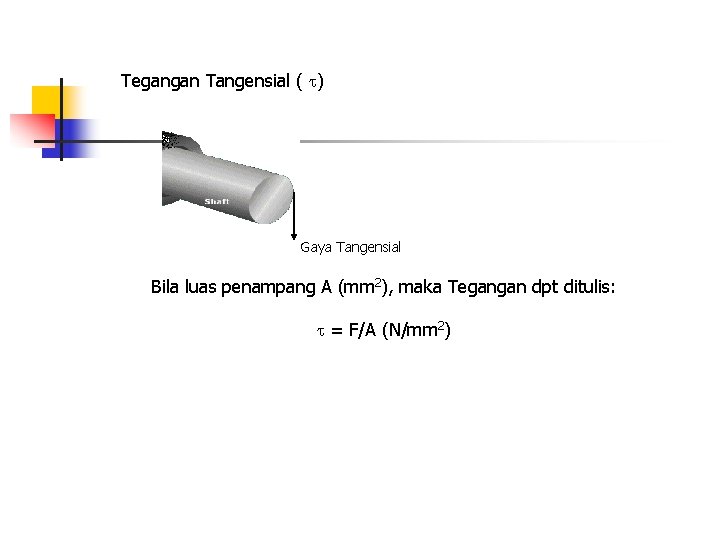
Tegangan Tangensial ( ) Gaya Tangensial Bila luas penampang A (mm 2), maka Tegangan dpt ditulis: = F/A (N/mm 2)

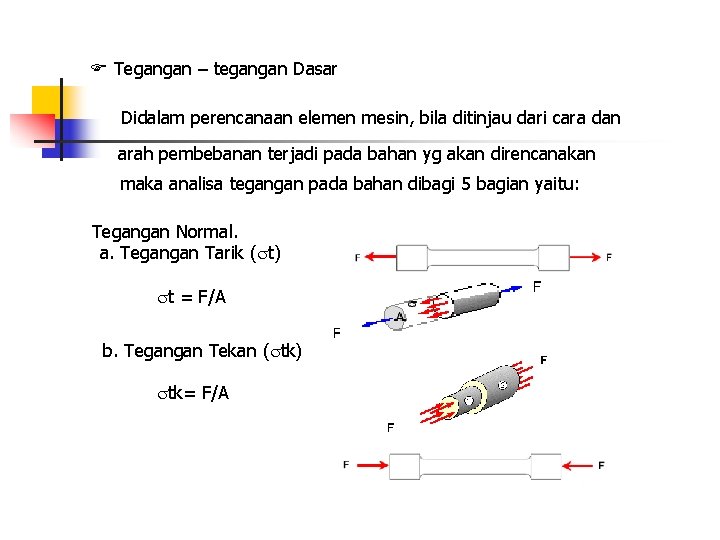
Tegangan – tegangan Dasar Didalam perencanaan elemen mesin, bila ditinjau dari cara dan arah pembebanan terjadi pada bahan yg akan direncanakan maka analisa tegangan pada bahan dibagi 5 bagian yaitu: Tegangan Normal. a. Tegangan Tarik ( t) t = F/A b. Tegangan Tekan ( tk) tk= F/A

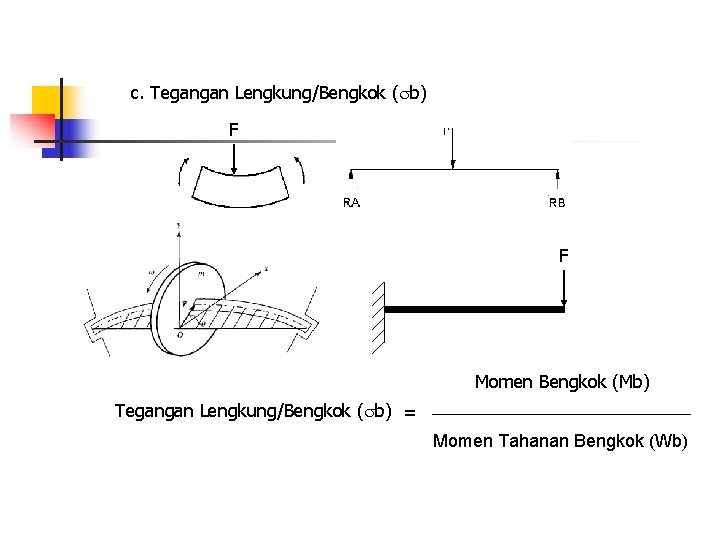
c. Tegangan Lengkung/Bengkok ( b) F F Momen Bengkok (Mb) Tegangan Lengkung/Bengkok ( b) = Momen Tahanan Bengkok (Wb)

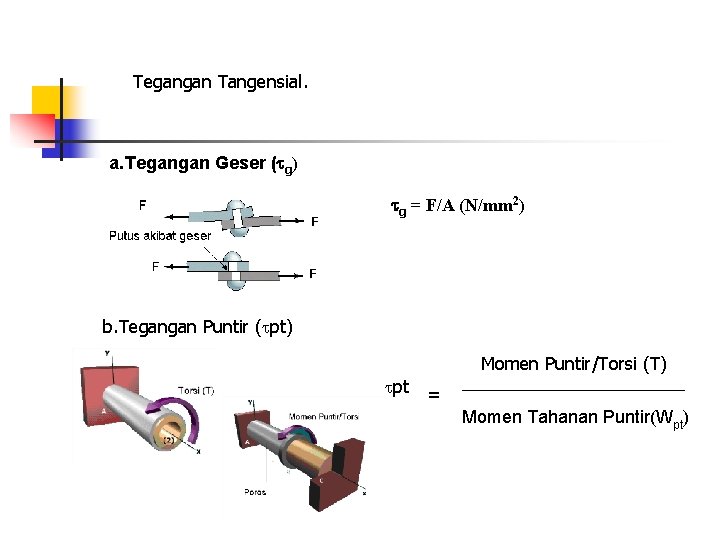
Tegangan Tangensial. a. Tegangan Geser ( g) g = F/A (N/mm 2) b. Tegangan Puntir ( pt) Momen Puntir/Torsi (T) pt = Momen Tahanan Puntir(Wpt)

Tegangan Kombinasi. Gaya F mengakibatkan tegangan normal ( ) Torsi (T) mengakibatkan tegangan tangensial ( ) Yang dimaksud teg. kombinasi adalah bila pada suatu batang menerima atau menahan dua jenis tegangan. Tegangan yg diterima pada batang yg sama berupa kombinasi antara tegangan normal dengan tegangan tangensial. Rumus-rumus Empiris Untuk Tegangan. g = 0, 8 t pt = 0, 6 t

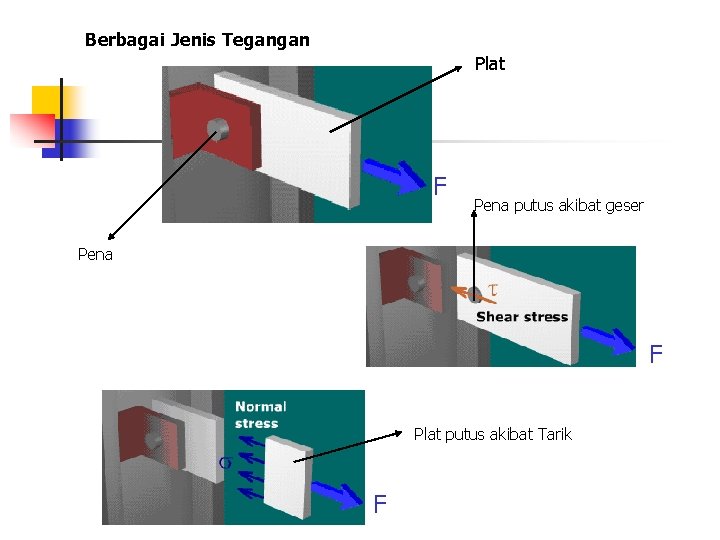
Berbagai Jenis Tegangan Plat F Pena putus akibat geser Pena F Plat putus akibat Tarik F

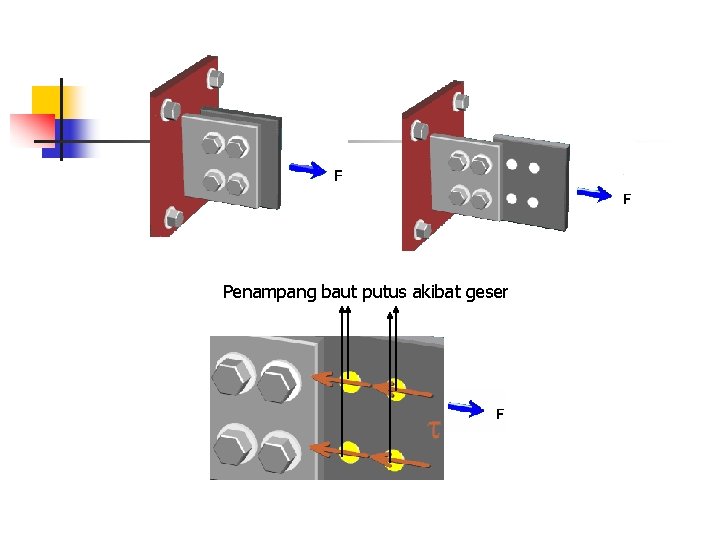
Penampang baut putus akibat geser

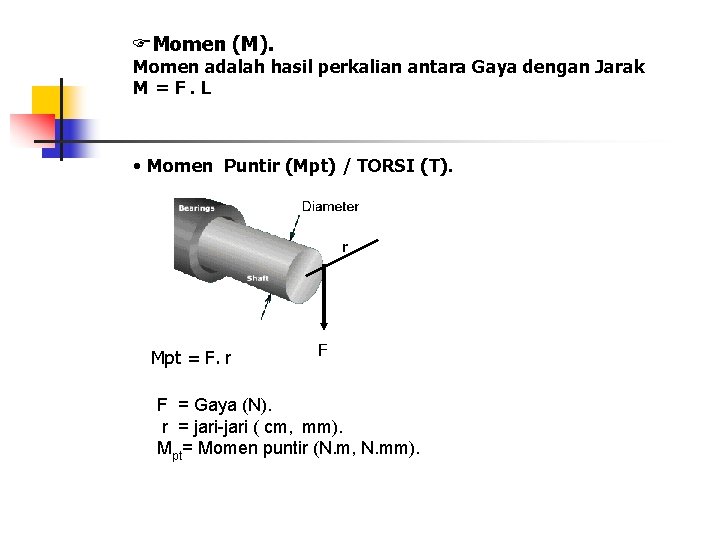
Momen (M). Momen adalah hasil perkalian antara Gaya dengan Jarak M=F. L • Momen Puntir (Mpt) / TORSI (T). r Mpt = F. r F F = Gaya (N). r = jari-jari ( cm, mm). Mpt= Momen puntir (N. m, N. mm).

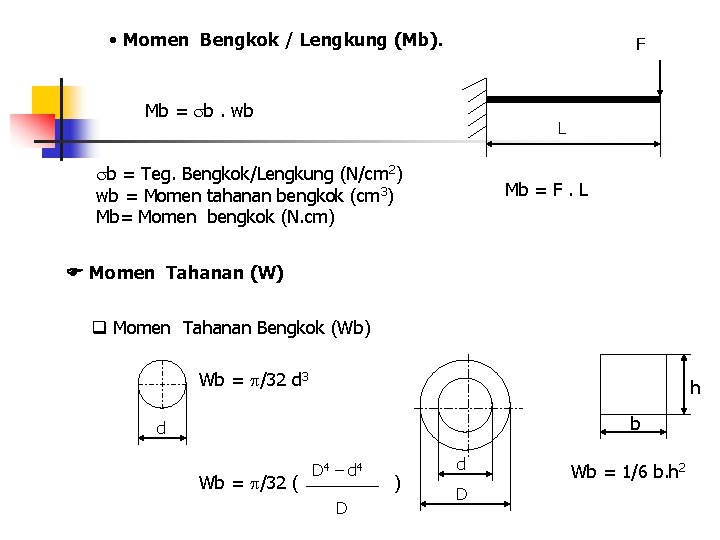
• Momen Bengkok / Lengkung (Mb). F Mb = b. wb L b = Teg. Bengkok/Lengkung (N/cm 2) wb = Momen tahanan bengkok (cm 3) Mb= Momen bengkok (N. cm) Mb = F. L Momen Tahanan (W) Momen Tahanan Bengkok (Wb) Wb = /32 d 3 h b d Wb = /32 ( D 4 – d 4 D ) d D Wb = 1/6 b. h 2

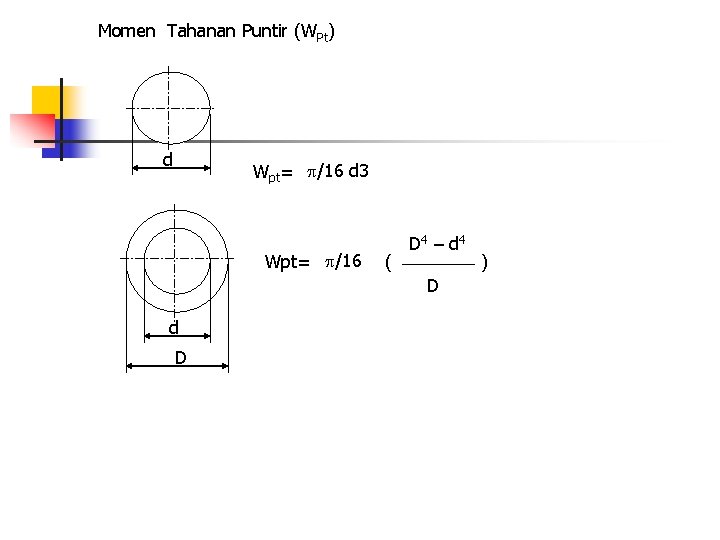
Momen Tahanan Puntir (WPt) d Wpt= /16 d 3 Wpt= /16 ( D 4 – d 4 D d D )

Diagram Tegangan dan Regangan ( & ). Bahan/Material yg diperjual belikan di pasaran kekuatan dari material tersebut sering diberikan dalam bentuk hasil pengujian, berupa Tegangan Tarik atau Kekerasan, dimana besar tegangan tarik ini selalu berhubungan dengan angka kekerasan dari suatu material/bahan. Besarnya tegangan tarik juga berhubungan dgn besarnya tegangan yg lain seperti: Teg. Lengkung, Teg. Geser dan Teg. puntir Hasil dari nilai teg. Tarik dari berbagai bahan/material diperoleh dari hasil percobaan yaitu dengan menarik material tersebut hingga putus. Dari hasil pengujian tarik untuk bahan maka diperoleh prilaku bahan/material dengan bentuk grafik. Bentuk dari grafik tersebut dinyatakan dalam grafik/diagram Tegangan dan Regangan

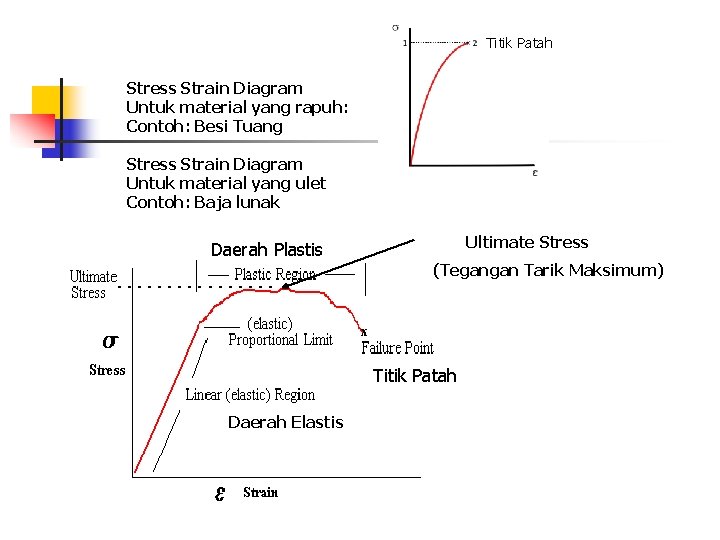
Titik Patah Stress Strain Diagram Untuk material yang rapuh: Contoh: Besi Tuang Stress Strain Diagram Untuk material yang ulet Contoh: Baja lunak Ultimate Stress Daerah Plastis (Tegangan Tarik Maksimum) Titik Patah Daerah Elastis

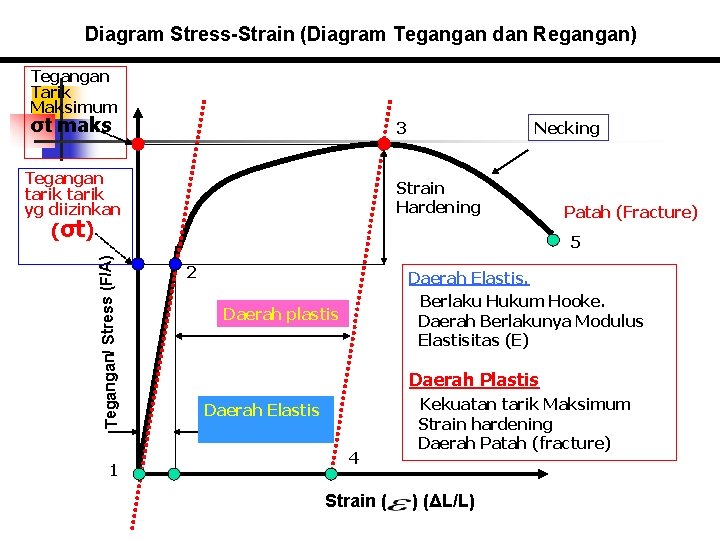
Diagram Stress-Strain (Diagram Tegangan dan Regangan) Tegangan Tarik Maksimum σt maks 3 Tegangan tarik yg diizinkan Necking Strain Hardening (σt) Patah (Fracture) Tegangan/ Stress (F/A) 5 1 2 Daerah Elastis. Berlaku Hukum Hooke. Daerah Berlakunya Modulus Elastisitas (E) Daerah plastis Daerah Plastis Daerah Elastis 4 Strain ( Kekuatan tarik Maksimum Strain hardening Daerah Patah (fracture) ) (ΔL/L)

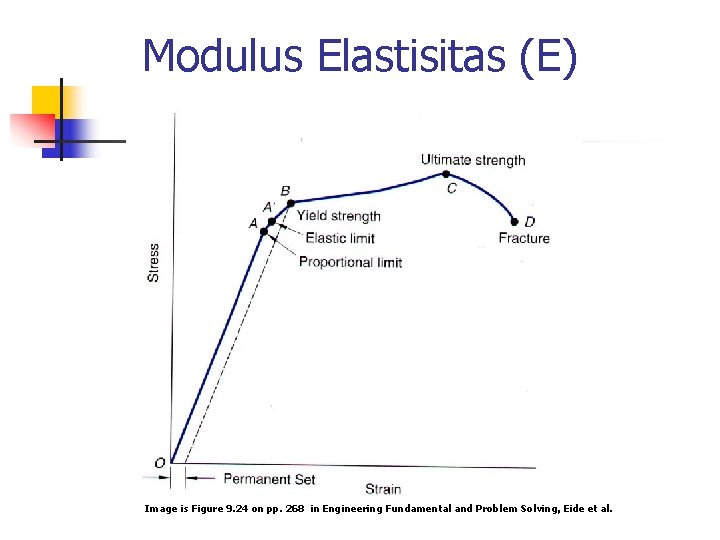
Modulus Elastisitas (E) Image is Figure 9. 24 on pp. 268 in Engineering Fundamental and Problem Solving, Eide et al.

Modulus Elastisitas (E) Material E, psi (lb/inc 2) Cold-rolled steel Cast iron Copper Aluminum Stainless steel Nickel Catatan : 30 x 106 16 x 106 10 x 106 27 x 106 30 x 106 E, Gpa (109 N/m 2) 210 110 70 190 210 N/m 2 = Pa N/mm 2 = Mpa (Mega Pascal) Table. 1 on pp. 269 in Engineering Fundamental and Problem Solving, Eide et al.

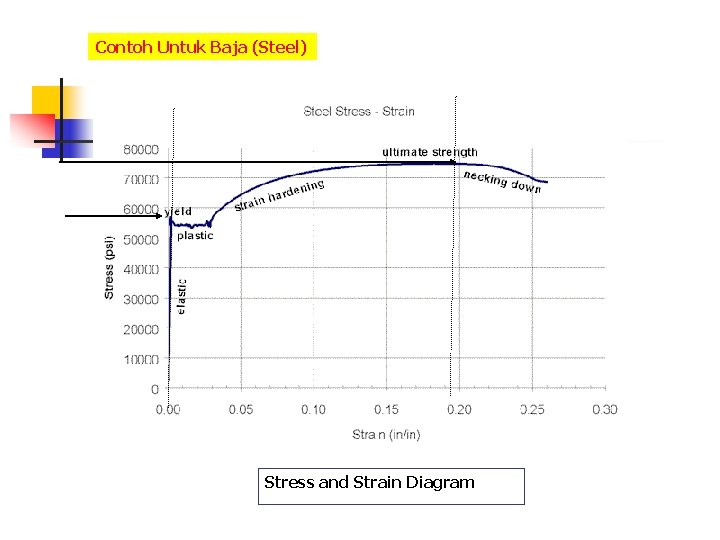
Contoh Untuk Baja (Steel) Stress and Strain Diagram

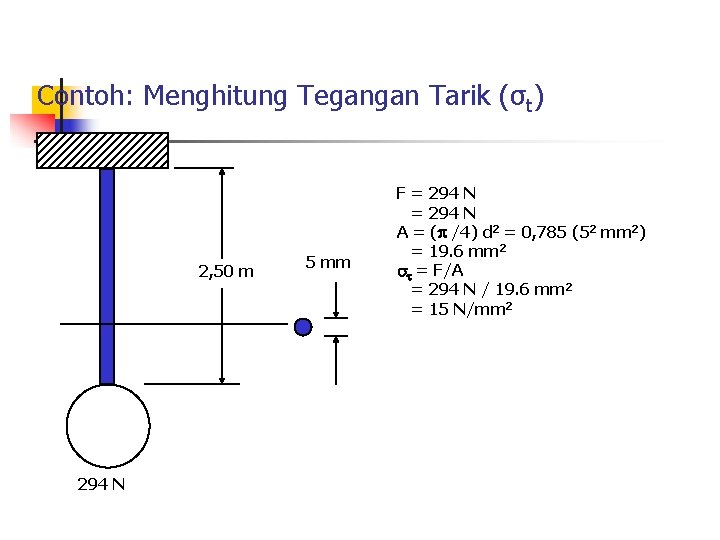
Contoh: Menghitung Tegangan Tarik (σt) 2, 50 m 294 N 5 mm F = 294 N A = ( /4) d 2 = 0, 785 (52 mm 2) = 19. 6 mm 2 = F/A = 294 N / 19. 6 mm 2 = 15 N/mm 2

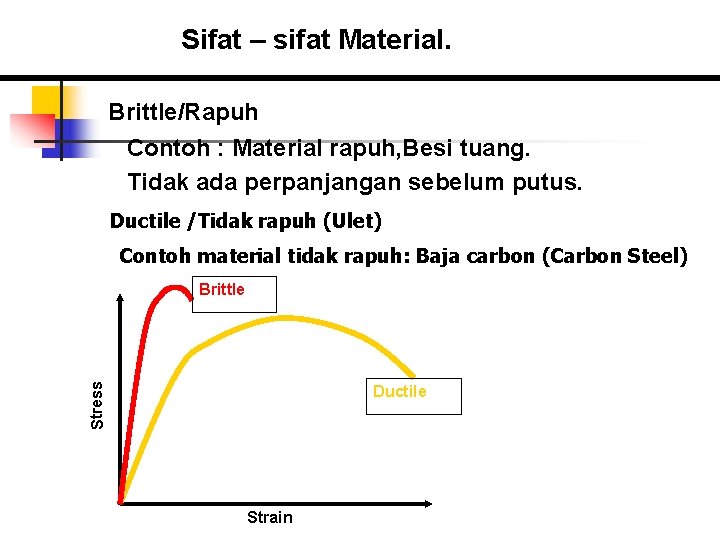
Sifat – sifat Material. Brittle/Rapuh Contoh : Material rapuh, Besi tuang. Tidak ada perpanjangan sebelum putus. Ductile /Tidak rapuh (Ulet) Contoh material tidak rapuh: Baja carbon (Carbon Steel) Stress Brittle Ductile Strain

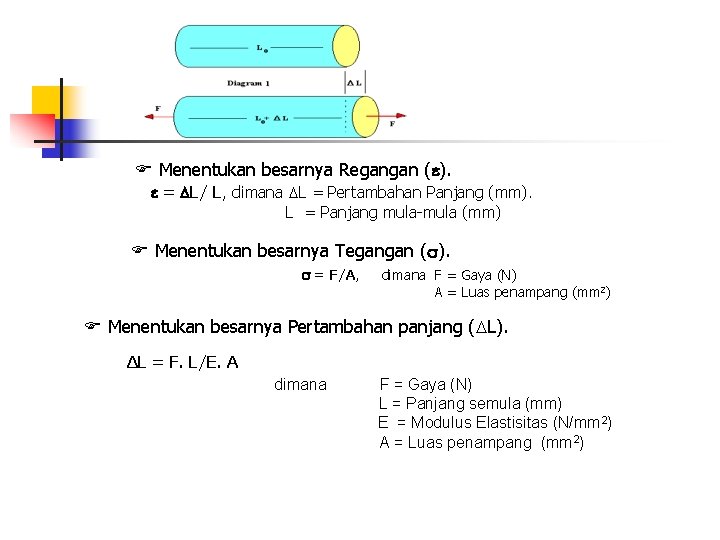
Menentukan besarnya Regangan ( ). = L/ L, dimana L = Pertambahan Panjang (mm). L = Panjang mula-mula (mm) Menentukan besarnya Tegangan ( ). = F/A, dimana F = Gaya (N) A = Luas penampang (mm 2) Menentukan besarnya Pertambahan panjang ( L). ΔL = F. L/E. A dimana F = Gaya (N) L = Panjang semula (mm) E = Modulus Elastisitas (N/mm 2) A = Luas penampang (mm 2)

Uraian dari persamaan didapat dalam bentuk lain : Є = ΔL/ L = F. L / E. A = F/ E. A = 1/ E. σ L Є = σ/E Atau E = σ/Є, Hukum Hook Menentukan besarnya Tegangan tarik maksimum ( t mak). Besarnya teg. maksimun untuk berbagai bahan dari hasil percobaan tarik biasanya selalu diambil sebagai symbol dari bahan , misalnya untuk baja: St 37 t mak = 37 kg/mm 2 = 370 N/mm 2 St 42 t mak = 42 kg/mm 2 = 420 N/mm 2 St 60 t mak = 60 kg/mm 2 = 600 N/mm 2

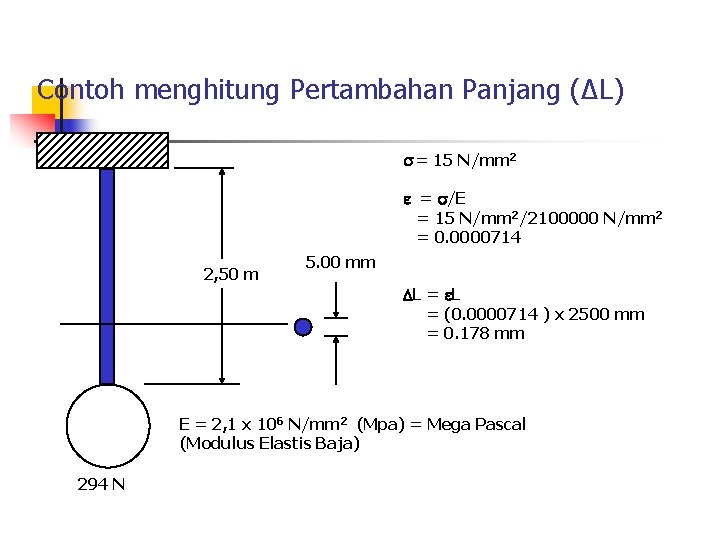
Contoh menghitung Pertambahan Panjang (ΔL) = 15 N/mm 2 = /E = 15 N/mm 2/2100000 N/mm 2 = 0. 0000714 2, 50 m 5. 00 mm L = (0. 0000714 ) x 2500 mm = 0. 178 mm E = 2, 1 x 106 N/mm 2 (Mpa) = Mega Pascal (Modulus Elastis Baja) 294 N

Tegangan tarikyang diizinkan /Tegangan Kerja. ( ). Setelah di ketahui besarnya teg. tarik dari berbagai bahan , maka didalam perencanaan elemen-elemen mesin sudah barang tentu dipilih suatu bahan yang aman untuk dipergunakan dalam merancang Elemen mesin tsb. Untuk itu dipilih suatu tegangan yg aman yang disebut dengan Tegangan yang diizinkan ( ) = t mak/ sf , dimana tmak = Tegangan tarik maksimum. sf = Faktor keamanan. Besarnya faktor keamanan yang diambil tergantung dari jenis pembebanan yang diterima.

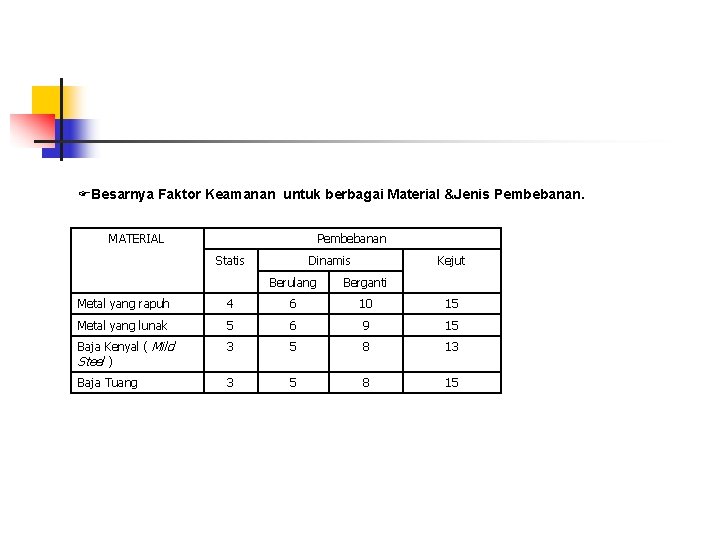
Besarnya Faktor Keamanan untuk berbagai Material &Jenis Pembebanan. MATERIAL Pembebanan Statis Dinamis Kejut Berulang Berganti Metal yang rapuh 4 6 10 15 Metal yang lunak 5 6 9 15 Baja Kenyal ( Mild Steel ) 3 5 8 13 Baja Tuang 3 5 8 15